Abstract
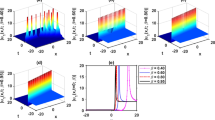
In this study, we discuss the application of an analytical technique namely modified homotopy analysis transform method (MHATM) for solving coupled one- dimensional time-fractional Keller-Segel (K-S) equations. The MHATM is a new analytical technique based on homotopy polynomial. We provide a convergence analysis of MHATM and the solution obtained by the proposed method is verified through different graphical representations. The results demonstrate that the proposed methodology is very useful and simple in the determination of the solution of the K-S equations of fractional order.
Similar content being viewed by others
References
Atangana, A.: Extension of the Sumudu homotopy perturbation method to an attractor for one-dimensional Keller-Segel equations. Appl. Math. Modell. 39, 2909–2916 (2015)
Atangana, A., Alabaraoye, E.: Solving a system of fractional partial differential equations arising in the model of HIV infection of CD4+ cells and attractor one-dimensional Keller-Segel equations. Adv. diff. equat. 94, 1–14 (2013)
Argyros, I.K.: Convergence and Applications of Newton-type Iterations. Springer-Verlag, New York (2008)
Anastassiou, G.A.: Fractional differentiation inequalities. Springer, New York (2009)
Anastassiou, G.A.: Fractional representation formulae and right fractional inequalities. Math. Comput. Modell. 54, 3098–3115 (2011)
Anastassiou, G.A.: Advanced fractional Taylor’s formula. J. Comput. Anal. Appl. 21(7), 1185–1204 (2016)
Caputo, V., Mainardi, F.: A new dissipation model based on memory mechanism. Pure. Appl. Geophys. 91, 134–147 (1971)
Hilfer, R.: Application of Fractional Calculus in Physics World Scientific (2000)
Jafari, H., Golbabai, A., Seifi, S., Sayevand, K.: Homotopy analysis method for solving multi-term linear and nonlinear diffusion—wave equations of fractional order. Comput. Math. Appl. 59(3), 1337–1344 (2010)
Keller, E.F., Segel, L.A.: Initiation of slime mold aggregation viewed as an instability. J. Theor. Bio. 26(3), 399–415 (1970)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and applications of fractional differential equations. Elsevier, The Netherlands (2006)
Khan, N.A., Jamil, M., Ara, A.: Approximate solutions to time fractional Schrodinger equation via homotopy analysis method. ISRN Math. Phys. 2012 (2012). Article ID 197068, 11 pages
Kumar, S.: A new analytical modelling for telegraph equation via Laplace transform. Appl. Math. Modell. 38(13), 3154–3163 (2014)
Kumar, S., Rashidi, M.M.: New analytical method for gas dynamic equation arising in shock fronts. Comput. Phy. Commun. 185(7), 1947–1954 (2014)
Kumar, S., Yildirim, A., Khan, Y., Leilei, W.: A fractional model of the diffusion equation and its analytical solution using Laplace transform. Sci. Iran 19(4), 1117–1123 (2012)
Liao, S.J.: A kind of approximate solution technique which does not depend upon small parameters (II): an application in fluid mechanics. Int. J. Nonlinear Mech. 32(5), 815–822 (1997)
Liao, S.J.: Beyond Perturbation: Introduction to the homotopy analysis method. Chapman and Hall CRC Press, Boca Raton (2003)
Liao, S.J.: On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 147(2), 499–513 (2004)
Liao, S.J., Tan, Y.: A general approach to obtain series solutions of nonlinear differential equations. Stud. Appl. Math. 119(4), 297–354 (2007)
Liao, S.J.: Notes on the homotopy analysis method: some definitions and theorems. Commun. Nonlinear Sci. Numer. Simulat. 14(4), 983–997 (2009)
Magrenan, A.A.: A new tool to study real dynamics: the convergence plane. Appl. Math. Comput. 248, 215–224 (2014)
Miller, K.S., Ross, B.: An introduction to the fractional integrals and derivativestheory and application (1993)
Momani, S., Odibat, Z.: Analytical solution of a time-fractional Navier-Stokes equation by Adomian decomposition method. Appl. Math. Comput. 177(2), 488–494 (2006)
Oldham, K.B., Spanier, J.: The Fractional Calculus. Academic Press, NY, USA (1974)
Odibat, Z., Momani, S., Xu, H.: A reliable algorithm of homotopy analysis method for solving nonlinear fractional differential equations. Appl. Math. Modell. 34(3), 593–600 (2010)
Odibat, Z.: A study on the convergence of homotopy analysis method. Appl. Math. Comput. 217, 782–789 (2010)
Odibat, Z., Bataineh, A.S.: An adaptation of homotopy analysis method for reliable treatment of strongly nonlinear problems: construction of homotopy polynomials. Math. Meth. Appl. Sci. 38, 991–1000 (2015)
Podlubny, I.: Fractional differential equations. Academic, New York (1999)
Pandey, R.K., Singh, Om P., Baranwal, V.K.: An analytic algorithm for the spacetime fractional advectiondispersion equation. Comput. Phys. Commun. 182, 1134–1144 (2011)
Magin, R.L.: Fractional calculus in bio-engineering. Inc. Connecticut, Begell House Publisher (2006)
Samko, S.G., Kilbas, A.A., Marichev, O.I.: Fractional integrals and derivatives: Theory and applications. Gordon and Breach, New York (1993)
Vishal, K., Kumar, S., Das, S.: Application of homotopy analysis method for fractional swift Hohenberg equation-Revisited. Appl. Math. Modell. 36(8), 3630–3637 (2012)
Yang, X.J., Baleanu, D., Srivastava, H.M.: Local fractional integral transform and their applications. Elsevier Academic Press (2015)
Yang, X.J., Baleanu, D.: Fractal heat conduction problem solved by local fractional variation iteration method. Therm. Sci. 17, 625–628 (2013)
Zaslavsky, G.M.: Hamiltonian chaos and fractional dynamics. Oxford University Press (2005)
Zhang, X., Tang, B., He, Y.: Homotopy analysis method for higher-order fractional integro-differential equations. Comput. Math. Appl. 62(8), 3194–3203 (2011)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kumar, S., Kumar, A. & Argyros, I.K. A new analysis for the Keller-Segel model of fractional order. Numer Algor 75, 213–228 (2017). https://doi.org/10.1007/s11075-016-0202-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-016-0202-z