Investigations on several high-order ADI methods for time-space fractional diffusion equation

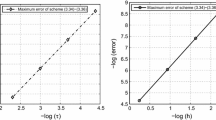
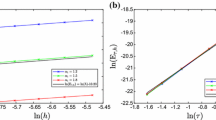
Abstract

The paper is devoted to the construction of high-precision unconditionally stable finite difference methods for solving time-space fractional diffusion equation with the Caputo fractional derivative (of order β, with β ∈ (0, 1)) in time and the Rimann-Liouville fractional derivatives (of order α, with α ∈ (1, 2]) in space. Two kinds of difference schemes with the approximation orders O(τ^2−β + h³) and O(τ² + h³) respectively are constructed. The stability and convergence are analyzed in detail. The obtained results are illustrated numerically by some examples, and a comparative study of several high-order schemes is also carried out.

Appendix

In this appendix, we present the proof of h(α; x) ≤ 0. Thus, we list the following lemma.

Lemma A.1

For anyx ∈ [0,π] andα ∈ (1, 2), we haveh(α; x) decreases withrespect toα,that is

$$\frac{\partial}{\partial \alpha}{h(\alpha; x)}\leq 0. $$

Proof

Taking the partial derivative of h(α, x) with respect to α, we have

$$ \frac{\partial}{\partial \alpha}{h(\alpha; x)}=L_{1}(\alpha;x)+\frac{\pi-x}{2}L_{2}(\alpha;x), $$

(1)

where

$$L_{1}(\alpha,x)=\frac{6\alpha-7}{24}\cos(A-x)+\frac{-6\alpha+ 13}{12}\cos(A)+\frac{6\alpha-19}{24}\cos(A+x),\qquad\qquad\quad $$

$$L_{2}(\alpha,x)=\frac{3\alpha^{2}-7\alpha}{24}\sin(A-x)+\frac{-3\alpha^{2}+ 13\alpha}{12}\sin(A)+\frac{3\alpha^{2}-19\alpha+ 24}{24}\sin(A+x) $$

with $A=\frac {\alpha (x-\pi )}{2}-x$.

Next, we estimate Eq. 28 via the following two steps.

I: :

We first consider L₁(α; x) ≤ 0. It is easy to obtain

$$ L_{1}(\alpha,x)=\frac{6\alpha-13}{12}\cos(A)\cos(x)+\frac{1}{2}\sin(A)\sin(x)+\frac{-6\alpha+ 13}{12}\cos(A). $$

(2)

For any x ∈ [π/2,π] and α ∈ (1, 2), it is obviously L₁(α; x) ≤ 0.

For any x ∈ [0,π/2) and α ∈ (1, 2), since

$$\frac{\partial}{\partial x}\left[\frac{6\alpha-13}{12}\cos A\cos x+\frac{1}{2}\sin A\sin x\right]\leq 0,$$

we have

$$\frac{6\alpha-13}{12}\cos A\cos x+\frac{1}{2}\sin A\sin x\leq \frac{6\alpha-13}{12}\cos \left( -\frac{\alpha\pi}{2}\right), $$

and combining with

$$\frac{-6\alpha+ 13}{12}\cos A\leq\frac{-6\alpha+ 13}{12}\cos\left( \frac{-\alpha\pi}{2}\right),$$

so we obtain L₁(α; x) ≤ 0.

II: :

We now consider L₂(α; x) ≤ 0. It is easy to obtain

$$ L_{2}(\alpha; x)=\frac{3\alpha^{2}-7\alpha}{12}\sin A\cos x+\frac{2-\alpha}{2}\sin\left( \frac{\alpha(x-\pi)}{2}\right)+\frac{-3\alpha^{2}+ 13\alpha}{12}\sin(A). $$

(3)

For any x ∈ [π/2,π] and α ∈ (1, 2), it is obviously L₂(α; x) ≤ 0.

For any x ∈ [0,π/2) and α ∈ (1, 2), we have

$$\begin{array}{@{}rcl@{}} L_{2}(\alpha; x)&=&\frac{3\alpha^{2}-7\alpha}{12}\sin A\cos x+\frac{2-\alpha}{2}\sin(A+x)+\frac{-3\alpha^{2}+ 13\alpha}{12}\sin(A)\\ &=&\frac{3\alpha^{2}-13\alpha}{12}\sin A(\cos x-1)+\sin A\cos x+\frac{2-\alpha}{2}\cos A\cos x\\ &\leq& 0. \end{array} $$

As a result of (I) and (II), we obtain the expected result.□