A class of upwind methods based on generalized eigenvectors for weakly hyperbolic systems

Abstract

In this article, a class of upwind schemes is proposed for systems, each of which yields an incomplete set of linearly independent eigenvectors. The theory of Jordan canonical forms is used to complete such sets through the addition of generalized eigenvectors. A modified Burgers’ system and its extensions generate δ,δ^′, δ^″,⋯,δⁿ waves as solutions. The performance of flux difference splitting-based numerical schemes is examined by considering various numerical examples. Since the flux Jacobian matrix of pressureless gas dynamics system also produces an incomplete set of linearly independent eigenvectors, a similar framework is adopted to construct a numerical algorithm for a pressureless gas dynamics system.

1 Introduction

The main motivation of this work is to develop upwind methods for weakly hyperbolic systems. A system is said to be hyperbolic if the Jacobian matrix of its flux vector has all the real eigenvalues with a complete set of linearly independent (LI) eigenvectors. A system is said to be weakly hyperbolic if two or more distinct eigenvalues become equal in some part of the flow field, resulting in an incomplete set of eigenvectors; for example, the formation of dry beds in shallow water equations leads to such situations [23, 31]. Similarly, a system is also said to be weakly hyperbolic if the corresponding flux Jacobian matrix contains an incomplete set of LI eigenvectors throughout the flow field; in that case, the Jacobian matrix is not diagonalizable but can be made similar to a Jordan matrix. Examples include modified Burgers’ system and system of pressureless gas dynamics equations. A square matrix J with a repeated eigenvalue $\lambda \in \mathbb {R}$ is called a Jordan matrix if each entry on the diagonal is λ, each entry on the super-diagonal is 1 and every other entry is zero. The construction process of some of the well-known upwind methods based on flux difference splitting (FDS) like the Roe scheme [24] requires a complete set of LI eigenvectors (also known as hyperbolicity property) which is missing for the considered systems. Thus, the application of such schemes is limited to those hyperbolic conservation laws that generate a complete set of LI eigenvectors. However, traditional simple and robust central solvers like Lax-Friedrichs [7, 18] or local Lax-Friedrichs (LLF) also known as the Rusanov method [25], can be effectively used to simulate the considered systems effortlessly; but, such solvers include a high dose of numerical diffusion resulting in smeared solutions. For example, the numerical investigations for multi-phase geometrical optics, a weakly hyperbolic system, is carried out using the Lax-Friedrichs method in [6] and with its second-order extension in [14].

In the present study, we start with a modified Burgers’ system [15], which is a simplified version of the pressureless system and can be derived from it by using a non-conservative form. This system is likely to have singular solutions like the delta distribution type solution. For this system, the matrix analysis of the flux Jacobian matrix shows that it has u as an eigenvalue with arithmetic multiplicity (AM) equal to 2, whereas the geometric multiplicity (GM) is only 1. Thus, the theory of Jordan canonical forms was used to construct a generalized basis for any column vector associated with the modified Burgers’ system. The ideas presented in this work were first tried out to develop an approximate Riemann solver in [9], utilizing the Toro and Vázquez [32] convection-pressure (C-P) splitting approach. However, later authors realized that reproducing an ideal Roe scheme might not be feasible with the considered C-P splitting approach as shown in [10]. Similarly, [8] can be regarded as a special case of the current work.

In Section 2, a detailed procedure that helps in generating generalized eigenvectors is presented. Section 3 deals with the construction process of an accurate upwind solver in the case of a modified Burgers’ system. For such systems, in [28], a Roe-like solver is developed by converting a weakly hyperbolic system into a strictly hyperbolic system. However, both [8] and [28] may not be applicable to a broader class of test cases and their applications are limited to sufficiently smooth non-Riemann data-based initial condition problems in the case of 2 × 2 modified Burgers’ and other extended systems. In order to check the performance of the Jordan-based FDS solver, several numerical examples including Riemann data-based initial problems are considered. The numerical results show that the FDS-based solver captures normal shock either exactly or within one interior zone and the accuracy of δ shocks turns out better than the traditional LLF method. Generally, accurate solvers tend to produce unphysical expansion shocks in the expansion region of the domain. To avoid unwanted expansion shocks, an entropy stable version is developed utilizing the theories given in [12, 29, 30]. Further, the entropy stable version retains the accuracy of the original method at shocks. In Section 4, an FDS-based solver is formulated for a 3 × 3 extended modified Burgers’ system [16, 26] that is known to develop more singular δ^′ shocks and this typically happens when the first equation develops normal shock as a solution. Through a numerical example, it is observed that the third component of the extended modified Burgers’ system may generate two beams of δ shocks in opposite directions, in addition to a vacuum state even for those cases that develop expansion waves as solutions in the first component of the system. Further, a 4 × 4 system is considered and numerical results indicate that the δ^″ shocks are even more singular than δ^′shocks.

In Section 5, a pressureless gas dynamics system is considered; this can be derived either from the Euler equations by letting the pressure goes to zero or from the microscopic level by allowing the temperature goes to zero in the Boltzmann equation. The present system is related to the sticky particle model of Zeldovich [34] in which the effect of gravitational forces is also considered. According to the theory of sticky particles, the particles stick together after collision and form a new bigger particle. The mass and velocity of a new particle are given by the laws of conservation of mass and momentum. Thus, the pressureless gas dynamics system is closely connected to systems that are helpful in explaining the formation of large-scale structures in the universe. One of the important works that is related to the study of a pressureless gas dynamics system at a discrete level using the kinetic theory framework is due to the contribution of Bouchut et al. [3]. Further, in a Godunov-type method [19], the author enforced upwinding based on the sign of a well-known Roe-average velocity. Similarly, a Roe-like method [28] is one of the latest works in the development of numerical methods for a system of pressureless gas dynamics but is computationally more expensive as compared to the FDS-based numerical method developed in this article. It is because of this reason that both the eigenvector structure and wave-strengths have to be computed in a Roe-like method, whereas the FDS-based solver is free from such complications and through a numerical example from [28]; it is observed that the FDS method captures δ shocks with almost double the accuracy as compared to a Roe-like method. However, the FDS method blows up for a class of numerical examples which helps in generating vacuum in the case of a pressureless system; precisely, for the u_L < 0 < u_R condition, this system is known to develop a vacuum region [19, 27]. In order to capture such phenomena, fluxes of the FDS method are further modified in case of stated condition. In Section 6, on a similar line as done in one-dimensional case, the FDS method is extended to a two-dimensional pressureless system. The computational results clearly show that the modified version preserves the positivity property of the density variable on both coarse and fine grids.

2 Jordan canonical forms

Every square matrix is similar to a triangular matrix with all the eigenvalues on its main diagonal. A square matrix is said to be similar to a diagonal matrix only if it has a complete set of LI eigenvectors. But every square matrix can be made similar to a Jordan matrix.

Re-visit of typical cases

Let a be an n × n matrix with n real eigenvalues, namely λ₁, λ₂, λ₃,⋯ ,λ_n. Now the following typical cases may arise:

Case 1::

When all λ_i, where 1 ≤ i ≤ n, are distinct. In this case, matrix A will have a complete set of LI eigenvectors, and hence will be similar to a diagonal matrix.

Case 2::

When some λ_i are equal, i.e., let λ₁ = λ₂ = λ₃ = ⋯ = λ_p = λ, where p is a natural number ≤ n. Then, any of the following sub-cases may happen.

Sub-case 1::

If the AM of an eigenvalue λ, which is p in the assumed case, is equal to the GM, and moreover, if this is true for all the subsets of equal eigenvalues, then the square matrix A will again be similar to a unique diagonal matrix.

Sub-case 2::

In the case in which GM is strictly less than AM, the LI set of eigenvectors will not be a complete one. In order to recover the full LI set of generalized eigenvectors, the theory of Jordan canonical forms is helpful; this is given below.

Procedure to find generalized eigenvectors

In this article, we mainly focus on systems that belong to the category discussed in Sub-case 2. If all the eigenvalues of a given matrix are equal, then the following steps need to be followed to recover the full set of LI generalized eigenvectors:

• (i) For an eigenvalue λ, compute the ranks of the matrices A − λI, (A − λI)², ⋯; then, find the least positive integer s such that rank(A − λI)^s = rank(A − λI)^s+ 1. There will be a single Jordan block only if s comes out equal to the dimension of a given matrix.

• (ii) Once s is equal to the dimension of a matrix, generalized eigenvectors can be computed from the system of equations AP = PJ, where,

  $$ {\boldsymbol J(\lambda)} = \left[\begin{array}{cccc} \ \lambda & 1 & \\[0.3em] \ & {\ddots} & {\ddots} & \\[0.3em] \ & & {\ddots} & 1 \\[0.3em] \ & & & \lambda \end{array}\right]_{s\times s}. \ $$

Let P equal to [X₁, X₂, X₃,...,X_s] be a set of column vectors that need to be evaluated. Then,

$$ \boldsymbol{A}\left[\boldsymbol{X}_{1}, \boldsymbol{X}_{2}, \boldsymbol{X}_{3},........., \boldsymbol{X}_{s}\right] \ = \ \left[\boldsymbol{X}_{1}, \boldsymbol{X}_{2}, \boldsymbol{X}_{3},........., \boldsymbol{X}_{s}\right] \left[\begin{array}{cccc} \ \lambda & 1 & \\[0.3em] \ & {\ddots} & {\ddots} & \\[0.3em] \ & & {\ddots} & 1 \\[0.3em] \ & & & \lambda \end{array}\right]_{s\times s} \ , $$

gives

$$ \begin{array}{cl} \boldsymbol{A}\boldsymbol{X}_{1} \ &= \ \lambda \boldsymbol{X}_{1}, \\ \boldsymbol{A}\boldsymbol{X}_{2} \ &= \ \lambda \boldsymbol{X}_{2} \ + \ \boldsymbol{X}_{1}, \\ \boldsymbol{A}\boldsymbol{X}_{3} \ &= \ \lambda \boldsymbol{X}_{3} \ + \ \boldsymbol{X}_{2}, \\ {\vdots} \\ \boldsymbol{A}\boldsymbol{X}_{s} \ &= \ \lambda \boldsymbol{X}_{s} \ + \ \boldsymbol{X}_{s-1}. \end{array} $$

(2.1)

Now, the eigenvectors can be computed along with the generalized eigenvectors from the system of relations (2.1).

3 Modified Burgers’ system

In this section, a 2 × 2 system of conservation laws are considered as given below:

$$ \begin{array}{@{}rcl@{}} \begin{array}{cl} \displaystyle u_{t} \ + \ \left( \frac{u^{2}}{2}\right)_{x} \ = \ 0,\\ \displaystyle v_{t} \ + \ (uv)_{x} \ = \ 0. \end{array} \end{array} $$

(3.1)

The system (3.1) is obtained from the following set of equations:

$$ \boldsymbol{A}_{t} \ + \ \left( \frac{\boldsymbol{A}^{2}}{2}\right)_{x} \ = \ \boldsymbol{0}, $$

(3.2)

where A is a lower triangular matrix with each diagonal entry as u and has the following form:

$$ \boldsymbol{A} \ = \ \left[\begin{array}{llll} \ u && 0 \\[0.3em] \ v && u \end{array}\right]. $$

Since the first equation of the system (3.1) is known to develop shock waves even for a sufficiently smooth initial data u(x,0), it is not obvious to solve the second equation of a considered system. In fact, K. T. Joseph [15] showed the existence of solutions to the system (3.1) by using the vanishing viscosity method by considering the following parabolic approximation:

$$ \begin{array}{@{}rcl@{}} \begin{array}{cl} \displaystyle u^{\epsilon}_{t} \ + \ \left( \frac{(u^{\epsilon})^{2}}{2}\right)_{x} \ = \ \frac{1}{2}\epsilon u^{\epsilon}_{xx},\\ \displaystyle v^{\epsilon}_{t} \ + \ \left( u^{\epsilon}v^{\epsilon}\right)_{x} = \ \frac{1}{2}\epsilon v^{\epsilon}_{xx}, \end{array} \end{array} $$

(3.3)

with the given discontinuous initial data. The solutions of (3.1) are then obtained by taking lim 𝜖 → 0 to the solutions of (3.3) in the sense of distributions. The system (3.2) can be recast into the following vector form, which is called the modified Burgers’ system:

$$ \frac{\partial \boldsymbol{U}}{\partial t} \ + \ \frac{\partial \boldsymbol{F}\left( \boldsymbol{U}\right)}{\partial x} \ = \ \boldsymbol{0}. $$

(3.4)

Here, $\boldsymbol {U} \ = \ \left [\begin {array}{c} \ u \\[0.3em] \ v \end {array}\right ]$ is a vector of conserved variables and $\boldsymbol {F}\left (\boldsymbol {U}\right ) \ = \ \left [\begin {array}{c} \ \frac {u^{2}}{2} \\[0.3em] \ u v \end {array}\right ]$ is a flux function. Further, (3.4) can be written in a quasi-linear form, which is as follows:

$$ \frac{\partial \boldsymbol{U}}{\partial t} \ + \ \boldsymbol{A}\left( \boldsymbol{U}\right) \frac{\partial \boldsymbol{U}}{\partial x} \ = \ \boldsymbol{0}, $$

(3.5)

with A (U) ≡A. The matrix A has a repeated eigenvalue u with AM equal to 2. For v≠ 0, the matrix analysis of A shows that the given system is weakly hyperbolic as it has only one eigenvector R₁ = (0,1)^t. Next, it is seen that rank(A − uI)² = 0 = rank(A − uI)³. Thus, s will be 2 in this case; so, there will be one Jordan block of order 2. On expanding the relation AP = PJ, it is shown as follows:

$$ \boldsymbol{A}[\boldsymbol{X}_{1} \ \ \boldsymbol{X}_{2}] \ = \ [\boldsymbol{X}_{1} \ \ \boldsymbol{X}_{2}] [\boldsymbol{J}_{1} \ \ \boldsymbol{J}_{2}], $$

(3.6)

where X₁ and X₂ are 2 × 1 column vectors that are required to be evaluated. Similarly, J₁ and J₂ are column vectors of the form as follows:

$$ \boldsymbol{J}_{1} = \left[\begin{array}{c} \ u \\[0.3em] \ 0 \end{array}\right]_{2 \times 1}, \ \boldsymbol{J}_{2} = \left[\begin{array}{c} \ 1 \\[0.3em] \ u \end{array}\right]_{2 \times 1} \ . $$

If (3.6) is expanded, the following relations are obtained as follows:

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \boldsymbol{A}\boldsymbol{X}_{1} \ = \ u \boldsymbol{X}_{1},\\ \boldsymbol{A}\boldsymbol{X}_{2} \ = \ u \boldsymbol{X}_{2} \ + \ \boldsymbol{X}_{1}. \end{array} \end{array} $$

(3.7)

From the first relation of (3.7), R₁ is obtained and on using this in the second relation as follows:

$$ \left[\begin{array}{cccc} \ u &0 \\[0.4em] \ v &u \end{array}\right] \left[\begin{array}{cc} \ x_{1} \\[0.4em] \ x_{2} \end{array}\right] \ = \ u \left[\begin{array}{cc} \ x_{1} \\[0.4em] \ x_{2} \end{array}\right] \ + \ \left[\begin{array}{cc} \ 0 \\[0.4em] \ 1 \end{array}\right], $$

$\boldsymbol {R}_{2} \ = \ (\frac {1}{v}, x_{2})^{t}$ is obtained as a generalized eigenvector, where .

3.1 Formulation of FDS scheme for modified Burgers’ system

Because of the non-linearity of the Jacobian matrix A, it is difficult to solve the system (3.5). But locally, inside each cell, the matrix A can be linearized to form a constant matrix $\boldsymbol {\bar {A}}$, which is now a function of the left- and right-state variables U_L and U_R, i.e., $\boldsymbol {\bar {A}} \ = \ \boldsymbol {\bar {A}}\left (\boldsymbol {U}_{L},\boldsymbol {U}_{R}\right )$. So, (3.5) becomes as follows:

$$ \frac{\partial \boldsymbol{U}}{\partial t} \ + \ \boldsymbol{\bar{A}} \frac{\partial \boldsymbol{U}} {\partial x} \ = \ \boldsymbol{0} . $$

(3.8)

On comparing (3.4) and (3.8), it is shown as follows:

$$ d\boldsymbol{F} \ = \ \boldsymbol{\bar{A}}d\boldsymbol{U}. $$

The finite difference analogue of the above differential relation is as follows:

$$ {\Delta}{\boldsymbol{F}} \ = \ \boldsymbol{\bar{A}}{\Delta}{\boldsymbol{U}}, $$

(3.9)

where ΔF = F_R −F_L and ΔU = U_R −U_L. In the above system of equations, the subscripts R and L represent the right and left states respectively. The relation (3.9) ensures the conservation property. As already explained, the present system is weakly hyperbolic but, on the basis of the above-mentioned procedure, a basis of eigenvectors and generalized eigenvectors can be constructed for the column vector ΔU, i.e.,

$$ {\Delta}{\boldsymbol{U}} \ = \ \sum\limits_{j = 1}^{2} \bar\alpha_{j}\boldsymbol{\bar{R}}_{j}, $$

(3.10)

where each $\bar {\alpha }_{j}$, 1 ≤ j ≤ 2, represents the wave strength attached with the respective LI eigenvectors corresponding to the given system. On using (3.10) in (3.9), it is shown as follows:

$$ {\Delta}{\boldsymbol{F}} \ = \ \boldsymbol{\bar{A}}\sum\limits_{j = 1}^{2} \bar\alpha_{j}\boldsymbol{\bar{R}}_{j}. $$

(3.11)

For a weakly hyperbolic system, $\boldsymbol {\bar {A}}$ is non-diagonalizable, resulting in as follows:

$$ \boldsymbol{\bar{A}} \boldsymbol{\bar{R}}_{j} \ \neq \ \bar \lambda_{j} \boldsymbol{\bar{R}}_{j}, $$

for some j’s. Since $\boldsymbol {\bar {R}}_{1}$ is an eigenvector and $\boldsymbol {\bar {R}}_{2}$ a generalized eigenvector, it is shown as follows:

$$ \boldsymbol{\bar{A}} \boldsymbol{\bar{R}}_{1} \ = \ \bar \lambda_{1} \boldsymbol{\bar{R}}_{1}, \ \boldsymbol{\bar{A}} \boldsymbol{\bar{R}}_{2} \ = \ \bar \lambda_{2} \boldsymbol{\bar{R}}_{2} \ + \ \boldsymbol{\bar{R}}_{1}. $$

On using the above relations in (3.11), it is shown as follows:

$$ {\Delta}{\boldsymbol{F}} \ = \ \bar\alpha_{1} \bar \lambda_{1} \boldsymbol{\bar{R}}_{1} \ + \ \bar\alpha_{2} \bar \lambda_{2} \boldsymbol{\bar{R}}_{2} \ + \ \bar\alpha_{2} \boldsymbol{\bar{R}}_{1}. $$

Next, the standard Courant splitting procedure to split eigenvalues is defined as follows:

$$ \bar \lambda^{+}_{j} - \bar \lambda^{-}_{j} \ = \ |\bar \lambda_{j}|. $$

After splitting each of the eigenvalues into a positive and a negative part, ΔF⁺ and ΔF⁻ can be written as follows:

$$ {\Delta}{\boldsymbol{F}}^{+} \ = \ \bar\alpha_{1} \bar \lambda^{+}_{1} \boldsymbol{\bar{R}}_{1} \ + \ \bar\alpha_{2} \bar \lambda^{+}_{2} \boldsymbol{\bar{R}}_{2} \ + \ \bar\alpha_{2} \boldsymbol{\bar{R}}_{1}^{\prime}, $$

(3.12)

$$ {\Delta}{\boldsymbol{F}}^{-} \ = \ \bar\alpha_{1} \bar \lambda^{-}_{1} \boldsymbol{\bar{R}}_{1} \ + \ \bar\alpha_{2} \bar \lambda^{-}_{2} \boldsymbol{\bar{R}}_{2} \ + \ \bar\alpha_{2} \boldsymbol{\bar{R}}_{1}^{\prime}, $$

(3.13)

respectively, where $\boldsymbol {\bar {R}}_{1}^{\prime } = \frac {1}{2}\boldsymbol {\bar {R}}_{1}$. On using (3.12) and (3.13) in the upwinding part of the interface flux, it is shown as follows:

$$ \boldsymbol{F}_{I} \ = \ \frac{1}{2} \left[\boldsymbol{F}_{L} \ + \ \boldsymbol{F}_{R} \right] \ - \ \frac{1}{2} \left[ \left( {\Delta}{\boldsymbol{F}}^{+} \ - \ {\Delta}{\boldsymbol{F}}^{-}\right) \right], $$

the following relation is obtained as follows:

$$ \boldsymbol{F}_{I} \ = \ \frac{1}{2} \left[\boldsymbol{F}_{L} \ + \ \boldsymbol{F}_{R}\right] \ - \ \frac{1}{2} \sum\limits_{j = 1}^{2} \bar\alpha_{j} |\bar \lambda_{j}| \boldsymbol{\bar{R}}_{j}. $$

Since generalized eigenvector R₂ is not unique, it may lead to infinitely many variants of the interface flux F_I. To avoid uncertainty, $|\bar {\lambda }_{j}|$ is taken out from the summation as both eigenvalues are the same, i.e.,

$$ \begin{array}{@{}rcl@{}} \boldsymbol{F}_{I} \ &=& \ \frac{1}{2} \left[\boldsymbol{F}_{L} \ + \ \boldsymbol{F}_{R} \right] \ - \ \frac{1}{2} |\bar{\lambda}|\sum\limits_{j = 1}^{2} \bar\alpha_{j} \boldsymbol{\bar{R}}_{j}, \\ \ &=& \ \frac{1}{2} \left[\boldsymbol{F}_{L} \ + \ \boldsymbol{F}_{R} \right] \ - \ \frac{1}{2} |\bar{\lambda}|{\Delta}{\boldsymbol{U}}. \end{array} $$

(3.14)

For the present case, ΔU = (Δu, Δv)^t and $\bar {\lambda } = \bar {u}$. In order to solve (3.14) fully, the average value of u has to be found out from the relation ${\Delta }{\boldsymbol {F}} \ = \ \boldsymbol {\bar {A}} {\Delta }{\boldsymbol {U}}$. In expanded form, it can be written as follows:

$$ \left[\begin{array}{cc} {\Delta} (\frac{1}{2} u^{2}) \\[0.3em] {\Delta} (u v) \end{array}\right] \ = \ \left[\begin{array}{cccc} \bar u & 0 \\[0.3em] \bar v & \bar u \end{array}\right] \left[\begin{array}{cc} {\Delta} u \\[0.3em] {\Delta} v \end{array}\right]. $$

From the first equation, it is shown as follows:

$$ \frac{1}{2} {\Delta} \left( u^{2}\right) \ = \ \frac{1}{2} \left( {u^{2}_{R}} - {u^{2}_{L}}\right) \ = \ \bar u {\Delta}{u} \ = \ \bar{u}(u_{R} - u_{L}). $$

(3.15)

From (3.15), $\bar {u} \ = \ \frac {1}{2}(u_{L} + u_{R})$ is obtained and the average value of v does not need to be solved as the interface flux requires only $\bar {u}$ to be evaluated. The update formula in a finite volume framework can be written as follows:

$$ \boldsymbol{U}^{n+1}_{j} \ = \ \boldsymbol{U}^{n}_{j} \ - \ \frac{{\Delta} t}{{\Delta} x} \left[ \boldsymbol{F}^{n}_{j+\frac{1}{2}} \ - \ \boldsymbol{F}^{n}_{j-\frac{1}{2}} \right], $$

where the interface flux is defined as given in (3.14).

3.2 Numerical examples

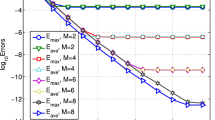
For a modified Burgers’ system, various numerical examples are considered to check the ability of the FDS scheme in resolving various flow features accurately. In the first numerical example, the initial conditions are chosen as (u_L, v_L) = (2,2), (u_R, v_R) = (4,− 2) with the initial discontinuity at location x_o = 0.0 and the numerical results are computed at the final time t = 0.15 units. For any Riemann data with u_L < u_R condition, the considered system evolves an expansion wave in the u variable and a constant zero state in the v variable. The computational domain x ∈ [− 1,1] is divided into 500 equally spaced cells and the CFL condition equal to 0.99 is used for all computations. The numerical results with the FDS scheme are given in Fig. 1 a and b. It is necessary to review the performance of any scheme on the refined mesh as numerical solvers may tend to generate oscillations or converge to wrong solutions as the mesh size goes towards zero. The above specified numerical example was used to authenticate the empirical convergence of a numerical solution towards an exact solution. The formula for finding the experimental order of convergence (EOC) is given below:

$$ s \ = \ \frac{\left( {\log} \ {E}_{\text{norm},h_{1}} \ - \ {\log} \ {E}_{\text{norm},h_{2}}\right)}{\left( {\log} \ h_{1} \ - \ {\log} \ h_{2}\right)}, $$

where s is the order of accuracy, $h_{1}, h_{2} = \frac {1}{2}h_{1}$ are grid spacings and E_norm,h is the error between the exact solution and the numerical solution expressed in some appropriate norm. In particular, for the discrete L¹ norm, it is shown as follows:

$$ E_{\text{norm},h} \ = \ E_{L^{1},h} \ = \ h \sum\limits_{j}|u_{j,\text{exact}} - u_{j,\text{numerical}}|. $$

In Table 1, the discrete L¹ error estimates are provided. It is observed that as the mesh size goes to zero the numerical solutions approach exact solutions under the L¹ error norm.

Fig. 1

a Formation of expansion wave in u variable and bv variable solution for a modified Burgers’ system

Table 1 L¹ error estimates for u variable using an expansion problem in the case of a modified Burgers’ system

Next, a test case is considered, as motivated from [21] with the following smooth initial conditions as follows:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{U}(x,0) \ = \ \left\{ \begin{array}{l} \frac{1}{2} + \sin(\pi x) \\ \pi \cos(\pi x) \end{array} \right. \ \ \forall x \in [0,2], \end{array} $$

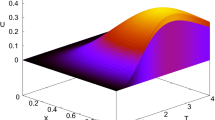
and periodic boundary conditions are imposed to compute solutions. Later, near time t = $\frac {3}{(2\pi )}$, the given system develops a normal shock and a δ shock in the u and v variables respectively. For the u variable, results with the FDS scheme are given in Fig. 2a and results using the local Lax-Friedrichs method are provided in Fig. 2b. The FDS scheme captures normal shock with one interior zone, whereas results with the LLF solver are diffusive. Similarly, for the v variable, results with both the schemes are presented in Fig. 3 a and b. Since the FDS scheme is an accurate scheme and as such schemes tend to produce unphysical expansion shocks in the expansion region of the domain, a test case that contains a sonic point with the initial conditions as (u_L, v_L) = (− 2,2), (u_R, v_R) = (4,− 2) at x_o = 0.2 is considered. For this problem, the final solutions are obtained at time t = 0.15 units. The numerical results with the FDS scheme are given in Fig. 4 a and b. To avoid expansion shocks, an entropy stable scheme is constructed using the theories developed in [12, 29, 30]. Let $E = \frac {1}{2}u^{2}$ be the entropy and $H = \frac {1}{3}u^{3}$ be the entropy flux function. Define v = ∇_UE(U) = (u,0)^t as the entropy variable. Now, the potential function ψ = 〈v,F〉− H comes out equal to $\frac {1}{6}u^{3}$, which further yields entropy conservative fluxes as given below:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{F}^{\text{EC}}_{1,j+\frac{1}{2}} \ &=& \ \frac{1}{6}(2\bar{u}^{2}_{j+\frac{1}{2}} + \bar{u^{2}}_{j+\frac{1}{2}}), \\ \boldsymbol{F}^{\text{EC}}_{2,j+\frac{1}{2}} \ &=& \ \textrm{arbitrary.} \end{array} $$

Next, the entropy stable scheme EC-FDS is formulated utilizing the idea developed in [12] and after employing similar techniques, the interface fluxes are written as follows:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{F}^{\text{EC-FDS}}_{1,j+\frac{1}{2}} \ &=& \ \frac{1}{6}({u}^{2}_{j} + u_{j}u_{j+1} + {u}^{2}_{j+1}) - \frac{1}{2}(\alpha_{\text{FDS}} + \frac{1}{6}|{\Delta}{u}|){\Delta}{u}, \\ \boldsymbol{F}^{\text{EC-FDS}}_{2,j+\frac{1}{2}} \ &=& \ \frac{1}{2}(u_{j} v_{j} + u_{j+1} v_{j+1}) \ - \ \frac{1}{2}\alpha_{\text{FDS}}{\Delta}{v}, \end{array} $$

where $\alpha _{\text {FDS}} \ = \ |\bar {u}|_{j+\frac {1}{2}}$. In Table 2, L¹ error estimates are provided with the EC-FDS scheme utilizing test case one. On comparing Tables 1 and 2, it is recognized that the EC-FDS solver brings a little extra diffusion in comparison to the original FDS-based solver in the expansion region of the flow field but still performs slightly better than the LLF method. Further, the performance of both FDS and EC-FDS are compared for a test case that develops a standing shock in the u variable. Both the solvers perform identically at normal and δ shocks as shown in Fig. 5 a and b. Subsequently, with the EC-FDS scheme, unphysical expansion shocks are overcome as evident from Fig. 6 a and b.

Fig. 2

Formation of normal shock in u variable a with FDS scheme and b result with LLF method for a modified Burgers’ system

Fig. 3

Formation of δ shock in v variable a with FDS scheme and b result with LLF method for a modified Burgers’ system

Fig. 4

a Sonic point problem, results for u variable and b results for v variable with FDS-based scheme for a modified Burgers’ system

Table 2 L¹ error estimates for u variable for a first-test problem in the case of a modified Burgers’ system

Fig. 5

a Results for u variable and b results for v variable with FDS and EC-FDS schemes for a modified Burgers’ system

Fig. 6

a Sonic point problem, results for u variable and b results for v variable with EC-FDS scheme for a modified Burgers’ system

4 Extended modified Burgers’ system

In this section, a 3 × 3 system of conservation laws is considered as follows:

$$ \begin{array}{@{}rcl@{}} u_{t} \ + \ (\frac{u^{2}}{2})_{x} \ &=& \ 0, \\ v_{t} \ + \ (uv)_{x} \ &=& \ 0,\\ w_{t} \ + \ (\frac{v^{2}}{2} + uw)_{x} \ &=& \ 0, \end{array} $$

(4.1)

as discussed in [16]. The main significance of this system is that it allows more singular δ^′ shocks to develop in the solution in addition to δ shocks. Similarly, by a change of variables u↦2u, v↦2v, w↦w, this system can be transformed into the following:

$$ \begin{array}{@{}rcl@{}} u_{t} \ + \ (u^{2})_{x} \ &=& \ 0, \\ v_{t} \ + \ (2uv)_{x} \ &=& \ 0, \\ w_{t} \ + \ 2(v^{2} + uw)_{x} \ &=& \ 0, \end{array} $$

which is studied in [26]. To maintain consistency with a 2 × 2 system as discussed in the previous section, (4.1) is used to construct an upwind solver utilizing the idea developed in the last section. In vector form, the considered system can be written as follows:

$$ \frac{\partial \boldsymbol{U}}{\partial t} \ + \ \frac{\partial \boldsymbol{F}\left( \boldsymbol{U}\right)}{\partial x} \ = \ \boldsymbol{0}, $$

where U = (u,v,w)^t and $\boldsymbol {F} \ = \ (\frac {u^{2}}{2}, uv, \frac {v^{2}}{2} + uw)^{t}$. Similarly, the given system can be written in quasi-linear form as follows:

$$ \frac{\partial \boldsymbol{U}}{\partial t} \ + \ \boldsymbol{A}\frac{\partial \boldsymbol{U}}{\partial x} \ = \ \boldsymbol{0}, $$

where,

$$ \ \boldsymbol{A} = \left[\begin{array}{lll} \ u & 0 & 0 \\[0.3em] \ v & u & 0 \\[0.3em] \ w & v & u \end{array}\right], $$

is a 3 × 3 Jacobian matrix with u as a repeated eigenvalue of multiplicity 3. Moreover, for v≠ 0, A has only one eigenvector e₃ and generalized eigenvectors can be calculated from the following relations:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{A} \boldsymbol{X}_{1} \ &=& \ u \boldsymbol{X}_{1}, \\ \boldsymbol{A} \boldsymbol{X}_{2} \ &=& \ u \boldsymbol{X}_{2} \ + \ \boldsymbol{X}_{1},\\ \boldsymbol{A} \boldsymbol{X}_{3} \ &=& \ u \boldsymbol{X}_{3} \ + \ \boldsymbol{X}_{2}. \end{array} $$

(4.2)

On solving the first relation of (4.2), X₁ = R₁ = e₃ = (0,0,1)^t is obtained as an eigenvector. On expanding and solving the second relation, it is shown as follows:

$$ \left[\begin{array}{lll} \ u & 0 & 0 \\[0.1em] \ v & u & 0 \\[0.1em] \ w & v & u \end{array}\right] \left[\begin{array}{l} x_{1} \\[0.1em] x_{2} \\[0.1em] x_{3} \\[0.1em] \end{array}\right] \ = \ u \left[\begin{array}{l} x_{1} \\[0.1em] x_{2} \\[0.1em] x_{3} \end{array}\right] \ + \ \left[\begin{array}{l} 0 \\[0.1em] 0 \\[0.1em] 1 \end{array}\right], $$

$\boldsymbol {X}_{2} \ =\ \boldsymbol {R}_{2} \ =\ (0,\frac {1}{v},x_{3})^{t}$ is obtained as a first generalized eigenvector. Again, on solving the third relation, an other generalized eigenvector comes out as $\boldsymbol {X}_{3} \ =\ \boldsymbol {R}_{3} \ = \ (\frac {1}{v^{2}}, \ \frac {x_{3}}{v} + \frac {w}{v^{3}}, \ y_{3})^{t}$, where x₃ and y₃ ∈IR. Let P be the matrix formed using eigenvectors and generalized eigenvectors as column vectors, i.e.,

$$ \boldsymbol{P} \ = \ \left[\begin{array}{cccc} \ 0 & 0 & \frac{1}{v^{2}} \\[0.1em] \ 0 & \frac{1}{v} & \frac{x_{3}}{v} - \frac{w}{v^{3}} \\[0.1em] \ 1 & x_{3} & y_{3} \end{array}\right], $$

then, ${\det }(\boldsymbol {P}) \ = \ -\frac {1}{v^{3}} \neq 0 \ \text {for} \ v \neq 0$.

4.1 Formulation of FDS scheme for extended modified Burgers’ system

Since ${\Delta }{\boldsymbol {F}} \ = \ \boldsymbol {\bar {A}}{\Delta }{\boldsymbol {U}}$ and

$$ \ {\Delta}{\boldsymbol{U}} \ = \ \sum\limits_{j = 1}^{3} \bar\alpha_{j}\boldsymbol{\bar{R}}_{j}, \ \text{therefore} \ {\Delta}{\boldsymbol{F}} \ = \ \boldsymbol{\bar{A}}\sum\limits_{j = 1}^{3} \bar\alpha_{j}\boldsymbol{\bar{R}}_{j}. $$

In the expanded form ΔF, on using (4.2), it can be written as follows:

$$ {\Delta}{\boldsymbol{F}} \ = \ \bar\alpha_{1} \bar \lambda \boldsymbol{\bar{R}}_{1} \ + \ \bar\alpha_{2}(\bar \lambda \boldsymbol{\bar{R}}_{2} \ + \ \boldsymbol{\bar{R}}_{1}) \ + \ \bar\alpha_{3}(\bar\lambda \boldsymbol{\bar{R}}_{3} \ + \ \boldsymbol{\bar{R}}_{2}) $$

Now, after splitting an eigenvalue $\bar {\lambda } = \bar {u}$ into a positive part and a negative part, ΔF⁺ and ΔF⁻ are given by the following:

$$ \begin{array}{@{}rcl@{}} {\Delta}{\boldsymbol{F}}^{+} \ &=& \ \bar\alpha_{1} \bar \lambda^{+} \boldsymbol{\bar{R}}_{1} \ + \ \bar\alpha_{2}(\bar \lambda^{+} \boldsymbol{\bar{R}}_{2} \ + \ \boldsymbol{\bar{R}}_{1}^{\prime}) \ + \ \bar\alpha_{3}(\bar\lambda^{+} \boldsymbol{\bar{R}}_{3} \ + \ \boldsymbol{\bar{R}}_{2}^{\prime}), \\ {\Delta}{\boldsymbol{F}}^{-} \ &=& \ \bar\alpha_{1} \bar \lambda^{-} \boldsymbol{\bar{R}}_{1} \ + \ \bar\alpha_{2}(\bar \lambda^{-} \boldsymbol{\bar{R}}_{2} \ + \ \boldsymbol{\bar{R}}_{1}^{\prime}) \ + \ \bar\alpha_{3}(\bar\lambda^{-} \boldsymbol{\bar{R}}_{3}\ + \ \boldsymbol{\bar{R}}_{2}^{\prime}), \end{array} $$

where $\boldsymbol {\bar {R}}_{1}^{\prime } = \frac {1}{2}\boldsymbol {\bar {R}}_{1}$ and $\boldsymbol {\bar {R}}_{2}^{\prime } = \frac {1}{2}\boldsymbol {\bar {R}}_{2}$. Now, the diffusion part of the FDS scheme for the extended modified Burgers’ system is given as follows:

$$ {\Delta}{\boldsymbol{F}}^{+} - {\Delta}{\boldsymbol{F}}^{-} \ = \ |\bar \lambda|{\Delta}{\boldsymbol{U}}, $$

where ΔU = (Δu,Δv,Δw)^t and the average value $\bar {u}$ is found from the first equation of the relation ${\Delta }{\boldsymbol {F}} \ = \ \boldsymbol {\bar {A}}{\Delta }{\boldsymbol {U}}$ and is equal to $\frac {1}{2}(u_{L}+u_{R})$.

Remark 4.1

It is shown that for v≠ 0, the Jacobian matrix A possesses only one eigenvector e₃ but in numerical examples, v can be identically zero throughout the domain and in that case, there will be two eigenvectors R₁ = e₂ and R₂ = e₃ corresponding to the matrix A. Then, the Jordan matrix will be made up of two smaller Jordan blocks of order one and two respectively and R₂ = e₃ forms a Jordan chain of order two. Further, on using a similar procedure as done earlier, the required generalized eigenvector X₃ = R₃ can be found using the relation AX₃ = uX₃ + R₂ and after simplifications, $\boldsymbol {R}_{3} \ \textrm {comes out equal to} \ (\frac {1}{w}, x_{2}, x_{3})^{t}$. Even for this case, ${\Delta }{\boldsymbol {F}}^{+} - {\Delta }{\boldsymbol {F}}^{-} \ = \ |\bar \lambda |{\Delta }{\boldsymbol {U}}$ holds and R₁, R₂, and R₃ constitute a complete set of LI eigenvectors provided w≠ 0. Moreover,

$$ \boldsymbol{P}^{-1}\boldsymbol{A}\boldsymbol{P} \ = \ \left[\begin{array}{lll} \ u & 0 & 0 \\[0.2em] \ 0 & u & 1 \\[0.2em] \ 0 & 0 & u \end{array}\right]. $$

If v and w are zero, then the given system becomes a non-strict hyperbolic as then A has a complete set of LI eigenvectors.

4.2 Numerical examples

In the first numerical example, the following c^∞ initial conditions are taken as follows:

$$ \boldsymbol{U}(x,0) \ = \ \left[\begin{array}{cc} \sin(2\pi x) \\[0.1em] 2\pi \cos(2\pi x) \\[0.1em] -4\pi^{2} \sin(2\pi x) \end{array}\right], $$

and periodic boundary conditions are imposed to generate numerical solutions. At time $t=\frac {1}{2\pi }$, the first equation starts developing normal shock and at a later time t = 0.5, the solution forms standing shock. As δ^′ shocks are known to be more singular than δ shocks [16], a similar behavior is also observed in computational results with the FDS scheme as shown in Figs. 7 and 8. Further, a comparison of the FDS scheme with the LLF method is made for the w variable in Fig. 8b and from numerical results, it is clear that the FDS scheme produces results with almost double the strength as the LLF method. In the second numerical example, an initial Riemann data is selected in such a way that u_L > u_R and the v variable is chosen to be zero in the entire [− 1,1] domain, i.e., (u_L, v_L, w_L) = (3,0,2) and (u_R, v_R, w_R) = (1,0,2). All the numerical solutions are obtained at time t = 0.125 units. In [26], it is reported that if v_L + v_R = 0 and w_L + w_R≠ 0, the system develops a constant state in the v variable and δ shock in the w variable, which is justified by the FDS scheme as shown in Fig. 9 a and b. In the last numerical example, Riemann data with u_L < u_R, i.e., (u_L, v_L, w_L) = (1,2,2) and (u_R, v_R, w_R) = (3,2,2) with initial discontinuity placed at 0 was considered and all solutions were obtained at time t = 0.125 units. The numerical results for u variable and v variable with the FDS scheme are given in Fig. 10 a and b. Both results agree with the theory proposed in [26], but for the w variable, the numerical result as given in Fig. 11 exhibits two beams of delta shocks in opposite directions in addition to a vacuum state.

Fig. 7

a Results with FDS scheme for the formation of normal shock in u variable and b numerical results showing δ shocks with FDS scheme for an extended modified Burgers’ system

Fig. 8

Numerical results of $\delta ^{\prime }$ shocks a with FDS scheme and b with LLF method for an extended modified Burgers’ system

Fig. 9

Numerical results with FDS scheme showing a that v component is identically zero and b formation of δ shocks in w variable for v_L + v_R = 0 case

Fig. 10

Numerical results with FDS scheme showing a pure expansion in u variable and b formation of vacuum state in v variable for u_L < u_R initial conditions

Fig. 11

Numerical result with FDS scheme showing existence of δ shocks in opposite sides of w variable for u_L < u_R initial conditions

4.3 Further extended modified Burgers’ system

In this section, a 4 × 4 system known to produce δ^″ shocks [17, 22] that are more singular than δ^′ shocks is considered. This system of conservation laws is given as follows:

$$ \begin{array}{@{}rcl@{}} u_{t} \ + \ (\frac{u^{2}}{2})_{x} \ &=& \ 0, \ v_{t} \ + \ (uv)_{x} \ = \ 0, \\ w_{t} \ + \ (\frac{v^{2}}{2} + uw)_{x} \ &=& \ 0, \ z_{t} \ + \ (uz + vw)_{x} \ = \ 0. \end{array} $$

In vector form, the considered system can be written as follows:

$$ \frac{\partial \boldsymbol{U}}{\partial t} \ + \ \frac{\partial \boldsymbol{F}\left( \boldsymbol{U}\right)}{\partial x} \ = \ \boldsymbol{0}, $$

where U = (u,v,w,z)^t and $\boldsymbol {F} \ = \ (\frac {u^{2}}{2}, uv, \frac {v^{2}}{2} + uw, uz + vw)^{t}$. Similarly, the given system can be written in quasi-linear form as follows:

$$ \frac{\partial \boldsymbol{U}}{\partial t} \ + \ \boldsymbol{A}\frac{\partial \boldsymbol{U}}{\partial x} \ = \ \boldsymbol{0}, $$

and

$$ \boldsymbol{A} = \left[\begin{array}{llll} \ u & 0 & 0 & 0 \\[0.3em] \ v & u & 0 & 0 \\[0.3em] \ w & v & u & 0 \\[0.3em] \ z & w & v & u \end{array}\right]. $$

The eigenvalues corresponding to matrix A are u,u,u,u and for v≠ 0,w≠ 0,z≠ 0, rank(A − uI)⁴ = 0 = rank(A − uI)⁵, which means that matrix A possesses only one eigenvector. Thus, a Jordan chain of order 4 corresponding to matrix A is given as follows:

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \boldsymbol{A} \boldsymbol{X}_{1} \ = \ u \boldsymbol{X}_{1},\\ \boldsymbol{A} \boldsymbol{X}_{2} \ = \ u \boldsymbol{X}_{2} \ + \ \boldsymbol{X}_{1},\\ \boldsymbol{A} \boldsymbol{X}_{3} \ = \ u \boldsymbol{X}_{3} \ + \ \boldsymbol{X}_{2},\\ \boldsymbol{A} \boldsymbol{X}_{4} \ = \ u \boldsymbol{X}_{4} \ + \ \boldsymbol{X}_{3}. \end{array} \end{array} $$

(4.3)

On solving the first relation of (4.3), X₁ = R₁ = e₄ = (0,0,0,1)^t is obtained as an eigenvector. On expanding the second relation, it is shown as follows:

$$ \left[\begin{array}{llll} \ u & 0 & 0 & 0 \\[0.1em] \ v & u & 0 & 0 \\[0.1em] \ w & v & u & 0 \\[0.1em] \ z & w & v & u \end{array}\right] \left[\begin{array}{l} x_{1} \\[0.1em] x_{2} \\[0.1em] x_{3} \\[0.1em] x_{4} \end{array}\right] \ = \ u \left[\begin{array}{l} x_{1} \\[0.1em] x_{2} \\[0.1em] x_{3} \\[0.1em] x_{4} \end{array}\right] \ + \ \left[\begin{array}{l} 0 \\[0.1em] 0 \\[0.1em] 0 \\[0.1em] 1 \end{array}\right], $$

the first equation of which is an identity. From the second and third equations, x₁ = 0, x₂ = 0 are obtained and on further using these values in the fourth equation, x₃ comes out equal to $\frac {1}{v}$ where x₄ ∈IR is an arbitrary constant. Thus, the column vector $\boldsymbol {X}_{2}=\boldsymbol {R}_{2}= (0,0,\frac {1}{v},x_{4})$ will be, by definition, a generalized eigenvector. Other generalized eigenvectors can be found from successive relations and after simplifications, it is shown as follows:

$$ \boldsymbol{X}_{3} = \boldsymbol{R}_{3} = \left[\begin{array}{c} 0 \\[0.2em] \frac{1}{v^{2}} \\[0.2em] \frac{x_{4}}{v} - \frac{w}{v^{3}} \\[0.2em] y_{4} \end{array}\right], \ \boldsymbol{X}_{4} = \boldsymbol{R}_{4} = \left[\begin{array}{cc} \frac{1}{v^{3}} \\[0.2em] \frac{x_{4}}{v^{2}} - \frac{2w}{v^{4}} \\[0.2em] \frac{y_{4}}{v} - \frac{z}{v^{4}} - \frac{w x_{4}}{v^{3}} + \frac{2w^{2}}{v^{5}} \\[0.2em] t_{4} \end{array}\right], $$

where y₄, t₄ ∈IR. Let P be a matrix whose column vectors are R₁, R₂, R₃, and R₄, i.e.,

$$ \boldsymbol{P} \ = \ \left[\begin{array}{cccc} \ 0 & 0 & 0 & \frac{1}{v^{3}} \\[0.2em] \ 0 & 0 & \frac{1}{v^{2}} & \frac{x_{4}}{v^{2}} - \frac{2w}{v^{4}} \\[0.2em] \ 0 & \frac{1}{v} & \frac{x_{4}}{v} - \frac{w}{v^{3}} & \frac{y_{4}}{v} - \frac{z}{v^{4}} - \frac{w x_{4}}{v^{3}} + \frac{2w^{2}}{v^{5}} \\[0.2em] \ 1 & x_{4} & y_{4} & t_{4} \end{array}\right], $$

then, ${\det }(\boldsymbol {P}) = \frac {1}{v^{6}} \neq 0$. If v = 0 and w≠ 0,z≠ 0, then the matrix A has two LI eigenvectors e₃ and e₄ each of them forming a Jordan chain of order two. Thus, the required Jordan matrix is made up of two smaller 2 × 2 Jordan blocks. Similarly, ΔF⁺ and ΔF⁻ are given by the following:

$$ {\Delta}{\boldsymbol{F}}^{+} \ = \ \bar\alpha_{1} \bar \lambda^{+} \boldsymbol{\bar{R}}_{1} \ + \ \bar\alpha_{2}(\bar \lambda^{+} \boldsymbol{\bar{R}}_{2} \ + \ \boldsymbol{\bar{R}}_{1}^{\prime}) \ + \ \bar\alpha_{3}(\bar\lambda^{+} \boldsymbol{\bar{R}}_{3} \ + \ \boldsymbol{\bar{R}}_{2}^{\prime}) \ + \ \bar\alpha_{4}(\bar\lambda^{+} \boldsymbol{\bar{R}}_{4} \ + \ \boldsymbol{\bar{R}}_{3}^{\prime}), $$

and

$$ {\Delta}{\boldsymbol{F}}^{-} \ = \ \bar\alpha_{1} \bar \lambda^{-} \boldsymbol{\bar{R}}_{1} \ + \ \bar\alpha_{2}(\bar \lambda^{-} \boldsymbol{\bar{R}}_{2} \ + \ \boldsymbol{\bar{R}}_{1}^{\prime}) \ + \ \bar\alpha_{3}(\bar\lambda^{-} \boldsymbol{\bar{R}}_{3}\ + \ \boldsymbol{\bar{R}}_{2}^{\prime}) \ + \ \bar\alpha_{4}(\bar\lambda^{-} \boldsymbol{\bar{R}}_{4}\ + \ \boldsymbol{\bar{R}}_{3}^{\prime}). $$

On subtracting, the diffusion part of the further extended Burgers’ system comes out as follows:

$$ {\Delta}{\boldsymbol{F}}^{+} - {\Delta}{\boldsymbol{F}}^{-} \ = \ |\bar \lambda|{\Delta}{\boldsymbol{U}}, $$

and similarly the average value $\bar {\lambda } = \bar {u}$ is equal to $\frac {1}{2}(u_{L}+u_{R})$. Next, a numerical example is considered to demonstrate that δ^″ is more singular than δ^′. The numerical results corresponding to the initial conditions as given below for z variable with the FDS scheme are presented and compared with the LLF method as given in Fig. 12 a and b.

$$ \begin{array}{@{}rcl@{}} \boldsymbol{U}(x,0) \ = \ \left\{ \begin{array}{l} \frac{1}{2} + \sin(\pi x) \\ \pi \cos(\pi x) \\ -\pi^{2} \sin(\pi x) \\ -\pi^{3} \cos(\pi x) \end{array} \right. \ \ \ \forall x \in [0,2]. \end{array} $$

Fig. 12

a Formation of $\delta ^{\prime \prime }$ shocks in z variable with FDS scheme and b formation of $\delta ^{\prime \prime }$ shocks with LLF method

5 1-D pressureless system

Consider the one-dimensional pressureless gas dynamics system as follows:

$$ \frac{\partial \boldsymbol{U}}{\partial t} \ + \ \frac{\partial \boldsymbol{F} \left( \boldsymbol{U} \right)} {\partial x} \ = \ \boldsymbol{0}, $$

where U is the conserved variable vector and F (U) is the flux vector defined by the following:

$$ \boldsymbol{U} = \left[\begin{array}{cc} \rho \\[0.3em] \rho u \end{array}\right], \ \boldsymbol{F}(\boldsymbol{U}) = \left[\begin{array}{cc} \rho u \\[0.3em] \rho u^{2} \end{array}\right]. $$

This system can also be written in quasi-linear form as follows:

$$ \frac{\partial \boldsymbol{U}}{\partial t} \ + \ \boldsymbol{A} \frac{\partial \boldsymbol{U}} {\partial x} \ = \ \boldsymbol{0}. $$

Here, A is the Jacobian matrix for the pressureless system and is given by the following:

$$ \boldsymbol{A} = \left[\begin{array}{cc} \ 0 & 1 \\[0.3em] \ -u^{2} & 2u \end{array}\right]. $$

The eigenvalues corresponding to the flux Jacobian matrix A are λ₁ = λ₂ = u, and it has only one eigenvector X₁ = R₁ = (1,u)^t. A generalized eigenvector X₂ can be computed from the relation AX₂ = uX₂ + X₁, and after simplifications, X₂ = R₂ = (x₁,1 + ux₁)^t is obtained, where x₁ ∈IR.

5.1 Formulation of FDS scheme for pressureless system

On using similar concepts as explained in previous sections, it is shown as follows:

$$ {\Delta}{\boldsymbol{F}} \ = \ \bar\alpha_{1} \bar \lambda_{1} \boldsymbol{\bar{R}}_{1} \ + \ \bar\alpha_{2} \bar \lambda_{2} \boldsymbol{\bar{R}}_{2} \ + \ \bar\alpha_{2} \boldsymbol{\bar{R}}_{1} $$

Now, after splitting ΔF into a positive part and a negative part and further after simplifications, the interface flux can be written as follows:

$$ \boldsymbol{F}_{I} \ = \ \frac{1}{2} \left[\boldsymbol{F}_{L} + \boldsymbol{F}_{R} \right] \ - \ \frac{1}{2}|\bar u_{I}|{\Delta}{\boldsymbol{U}}, $$

or

$$ \boldsymbol{F}_{I} \ = \ \frac{1}{2} \left[\boldsymbol{F}_{L} + \boldsymbol{F}_{R} \right] \ - \ \frac{1}{2}|\bar u_{I}| \left[\begin{array}{cc} {\Delta}{\rho} \\[0.3em] {\Delta}(\rho u) \end{array}\right], $$

(5.1)

and Δ(ρu) is further equal to $\bar {u}{\Delta }{\rho } \ + \ \bar {\rho }{\Delta }{u}$, where $\bar {u}$ is some average of u_L and u_R, $\bar {\rho }$ is another average of ρ_L and ρ_R and both are to be determined. Expanding ${\Delta }{\boldsymbol {F}} = \boldsymbol {\bar {A}}{\Delta }{\boldsymbol {U}}$ to find the average values, i.e.,

$$ \left[\begin{array}{cc} {\Delta} (\rho u) \\[0.3em] {\Delta} (\rho u^{2}) \end{array}\right] \ = \ \left[\begin{array}{cc} 0 & 1 \\[0.3em] -{\bar u}^{2} & 2 \bar{u} \end{array}\right] \left[\begin{array}{cc} {\Delta} (\rho) \\[0.3em] {\Delta} (\rho u) \end{array}\right]. $$

(5.2)

The first relation of (5.2) is automatically satisfied for any average value. From the second relation, it is shown as follows:

$$ {\Delta}(\rho u^{2}) \ = \ -{\bar u}^{2} {\Delta} (\rho) \ + \ 2 \bar{u} {\Delta} (\rho u), $$

where,

$$ \begin{array}{@{}rcl@{}} {\Delta} (\rho) \ &=& \ (\rho)_{R} \ - \ (\rho)_{L}, \\ {\Delta} (\rho u) \ &=& \ (\rho u)_{R} \ - \ (\rho u)_{L}, \\ {\Delta} (\rho u^{2}) \ &=& \ (\rho u^{2})_{R} \ - \ (\rho u^{2})_{L}. \end{array} $$

After rearrangement of terms, it is shown as follows:

$$ {\bar{u}}^{2} {\Delta} (\rho) \ - \ 2 \bar{u} {\Delta} (\rho u) \ + \ {\Delta} (\rho u^{2})\ = \ 0, $$

which is a quadratic equation in $\bar {u}$, the solution of which is obtained as follows:

$$ \bar{u} \ = \ \frac{\sqrt{\rho_{L}} u_{L} \ \pm \ \sqrt{\rho_{R}} u_{R}} {\sqrt{\rho_{L}} \ \pm \ \sqrt{\rho_{R}}}. $$

The root having negative signs in both numerator and denominator is neglected as it is not physical and may become infinity as $\sqrt {\rho _{R}} \longmapsto \sqrt {\rho _{L}}$ or vice versa. Thus, the average value of u is defined as follows:

$$ \bar{u} \ = \ \frac{\sqrt{\rho_{L}} u_{L} \ + \ \sqrt{\rho_{R}} u_{R}} {\sqrt{\rho_{L}} \ + \ \sqrt{\rho_{R}}}. $$

On using $\bar {u}$ in the relation, it is shown as follows:

$$ \rho_{R}u_{R} - \rho_{L}u_{L} \ = \ \bar{u}(\rho_{R} - \rho_{L}) \ + \ \bar{\rho}(u_{R} - u_{L}), $$

the following relation is obtained as follows:

$$ \rho_{R}u_{R} - \rho_{L}u_{L} \ = \frac{\sqrt{\rho_{L}} u_{L} \ + \ \sqrt{\rho_{R}} u_{R}} {\sqrt{\rho_{L}} \ + \ \sqrt{\rho_{R}}}(\rho_{R} - \rho_{L}) \ + \ \bar{\rho}(u_{R} - u_{L}), $$

which further leads to $\bar {\rho } \ = \ \sqrt {\rho _{R}}\sqrt {\rho _{L}} \ = \ \sqrt {\rho _{R} \rho _{L}}$. As the interface flux (5.1) is now completely defined, the final update formula for the numerical scheme in the finite volume framework is written as follows:

$$ \boldsymbol{U}^{n+1}_{j} \ = \ \boldsymbol{U}^{n}_{j} \ - \ \frac{{\Delta} t}{{\Delta} x} \left[ \boldsymbol{F}^{n}_{j+\frac{1}{2}} \ - \ \boldsymbol{F}^{n}_{j-\frac{1}{2}} \right]. $$

5.2 Numerical examples

In the first numerical example, the initial data is selected with u_L > u_R condition and for such set of data, the system develops a δ shock and a normal shock in the density and velocity variables respectively. As an example, (ρ_L, u_L) = (1.0,2.0) and (ρ_R, u_R) = (0.5,1.0) are chosen as initial conditions with x_o = 0.0. Further, the computational domain [− 1.0,1.0] is divided into 200 equally spaced cells and all the final solutions are obtained at time t = 0.2 units. The exact solution corresponding to the u variable [27, pp. 12] is given as follows:

$$ \begin{array}{@{}rcl@{}} u(x,t) \ = \ \left\{ \begin{array}{l} u_{L}, \ \ \ \ \frac{x}{t}<\omega_{\delta} \\ \\ u_{\delta}, \ \ \ \ \frac{x}{t} = \omega_{\delta} \\ \\ u_{R}, \ \ \ \ \frac{x}{t} > \omega_{\delta} \end{array} \right. \ \ \ , \end{array} $$

where,

$$ \omega_{\delta} \ = \ u_{\delta} \ = \ \frac{\sqrt{\rho_{L}} u_{L} \ + \ \sqrt{\rho_{R}} u_{R}} {\sqrt{\rho_{L}} \ + \ \sqrt{\rho_{R}}}. $$

Similarly, the system develops δ waves in the density variable at the location x = ω_δt, where other states are given as follows:

$$ \begin{array}{@{}rcl@{}} \rho(x,t) \ = \ \left\{ \begin{array}{l} \rho_{L},\ \ \ \ \frac{x}{t} < \omega_{\delta} \\ \\ \rho_{R}, \ \ \ \ \frac {x}{t}> \omega_{\delta}. \end{array} \right. \end{array} $$

For the given set of data, ω_δ ≈ 1.585786 and after time t = 0.2 units, the initial discontinuity moves a distance approximately equal to 0.317157. The FDS solver generates a δ shock exactly at the location ω_δt as presented in Fig. 13a. Similarly, it captures a moving shock without any oscillations exactly at the ω_δt location in Fig. 13b.

Fig. 13

a Numerical results for density variable, formation of δ shocks and b formation of normal shocks in u variable with the FDS-based method for a pressureless system

Next, a test problem is taken from [1, Example 2] with u_L < 0 < u_R across a jump in the initial conditions. In the beginning, a discontinuity is placed at point x_o = 0.0 and the computational domain [− 0.5,0.5] is divided into 200 equally spaced cells. The details of an initial data are as follows:

$$ \begin{array}{@{}rcl@{}} \rho(x,0) \ = \ 0.5 \ , \ \ \ \ u(x,0) \ = \ \left\{ \begin{array}{l} -0.5, \ \ \ \ x < 0 \\ 0.4 , \ \ \ \ \ \ \ x > 0. \end{array} \right. \end{array} $$

The exact solution at time t = 0.5 is given as follows:

$$ \begin{array}{@{}rcl@{}} u(x,t) \ = \ \left\{ \begin{array}{l} -0.5, \ \ \ \ \ \ \ \ \ \ \ \ \ x < -0.25 \\ \text{undefined}, \ \ \ \ \ -0.25 <x<0.2 \\ 0.4, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x>0.2 . \end{array} \right. \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \rho(x,t) \ = \ \left\{ \begin{array}{l} 0, \ \ \ \ \ \ \ \ -0.25<x <0.2 \\ 0.5, \ \ \ \ \ \ \textrm{otherwise.} \end{array} \right. \end{array} $$

Since the system generates a vacuum state in the density variable, then there should not be any fluid particles in the region of the domain corresponding to such situations; this means that there must not be any particles with velocities ranging between (− 0.5,0.4) in the supposed domain. For this test case, the FDS solver fails to generate results. Thus, to avoid a blow-up of solutions, an additional diffusion is added to the interface velocity $\bar {\lambda }_{I} \ = \ \bar {u}_{I}$ using the concept of Harten’s [11] entropy fix, i.e.,

$$ \begin{array}{@{}rcl@{}} |\tilde{\lambda}_{I}| \ &=& \ |\bar{\lambda}_{I}| \ \ \ \ \ \ \ \ \ \ \ \ \ \quad \text{if} \ \ \ |\bar{\lambda}_{I}| \geq \epsilon \\ |\tilde{\lambda}_{I}| \ &=& \ \frac{1}{2}\left( \frac{\bar{\lambda}_{I}^{2}}{\epsilon} + \epsilon \right) \ \ \ \text{if} \ \ |\bar{\lambda}_{I}| < \epsilon, \end{array} $$

where 𝜖 is some arbitrary constant. It is observed that to avoid a blow-up of solutions, it is required to use 𝜖 ≥ 0.9 in the definition of entropy fix (E-fix) together with the FDS scheme. In Fig. 14a, positivity preserving density results with E-fix are presented, but the solver fails to satisfy the maximum principle as displayed in Fig. 14b.

Fig. 14

a Numerical results of density variable for the vacuum problem and b numerical results for u variable, FDS scheme with entropy fix

For u_L < 0 < u_R condition, the flow particles move away from the interface leading to a vacuum state. Thus, the interface flux is set as follows:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{F}_{I} \ = \ \left\{ \begin{array}{l} 0 \ \ \ \ \text{if} \ \ u_{L} < 0 < u_{R} \\ \frac{1}{2} \left[\boldsymbol{F}_{L} + \boldsymbol{F}_{R} \right] - \frac{1}{2}|\bar u_{I}|{\Delta}{\boldsymbol{U}}, \ \ \textrm{otherwise.} \end{array} \right. \end{array} $$

(5.3)

The modified FDS solver turns out to be reasonably satisfactory in handling both the vacuum state and the maximum principle without adding any extra diffusion mechanism to the algorithm as shown in Fig. 15 a and b.

Fig. 15

a Numerical results of density variable for the vacuum problem and b numerical results corresponding to u variable and the satisfaction of maximum principle with a modified FDS scheme

Similarly, a more complex test case is considered from [3, Example 1] to check the performance of the modified FDS scheme. The details of an aimed test case are provided as follows:

$$ \begin{array}{@{}rcl@{}} \rho(x,0) \ = \ 0.5 \ , \ \ \ \ u(x,0) \ = \ \left\{ \begin{array}{ll} -0.5, &\quad x < -0.5 \\ 0.4 , & \quad -0.5 <x<0 \\ 0.4 - x, & \quad 0 <x<0.8 \\ -0.4, & \quad x>0.8. \end{array} \right. \end{array} $$

The exact solution at time t = 0.5 is given as follows:

$$ \begin{array}{@{}rcl@{}} u(x,t) \ = \ \left\{ \begin{array}{ll} -0.5, & \quad x < -0.75 \\ \text{undefined}, & \quad -0.75 <x<-0.3 \\ 0.4, & \quad -0.3<x<0.2 \\ 0.8 -2x, & \quad 0.2 <x<0.6 \\ -0.4, & \quad x>0.6 \end{array} \right. \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \rho(x,t) \ = \ \left\{ \begin{array}{l} 0, \ \ \ \ \ \ \ \ -0.75<x <-0.3 \\ 1, \ \ \ \ \ \ \ \ \ 0.2 <x<-0.6 \\ 0.5, \ \ \ \ \ \ \textrm{otherwise.} \end{array} \right. \end{array} $$

The numerical results with 200 grid points are presented in Fig. 16 a and b. The modified FDS scheme appears to generate some undesired overshoots in the density variable. It is observed that such behavior plagues most of the well-known numerical algorithms; for example, a numerical study of a Godunov-type flux [19] and a Rusanov method also yield similar overshoots as shown in Figs. 17a and 18a respectively. In addition to this, we emphasize that the Rusanov method also indicates the presence of fluid particles in the vacuum region of the domain in Fig. 18b, whereas a Godunov-type flux correctly preserves the maximum principle in Fig. 17b. The appearance of overshoots in the density variable with most of the algorithms is probably due to the premature sensing of the presence of a “shock point” in the u variable; in other words, at x = ξ = 0.4, u(ξ) = 0 and in the deleted neighborhood of u(ξ), u_L > u_R which is the required condition to form a δ shock in the density variable. If the present test case is run for a time t ≥ 1 units, the system develops a standing shock in the u variable and a δ shock in the density variable precisely at point ξ = 0.4. Next, a test case with initial conditions as given in [28, Eq. (116)] is simulated with the FDS-based scheme. It is observed that the present scheme captures δ shocks with almost double the accuracy in Fig. 19a as compared to the results shown in Figure 4(a) of [28, pp. 132]. Similarly, the FDS-based scheme captures a normal shock at the right position in Fig. 19b. Finally, the performance of the newly constructed scheme is examined on a special case [2, Example 2.1] with ρ^o = 2δ, (ρu)^o = q^o ≡ 0 as initial conditions. For this particular test problem, the uniqueness of a solution set is not granted by the authors. To perform computations, the δ distribution is replaced with the $\frac {1}{\pi }\frac {\epsilon }{x^{2} + {\epsilon }^{2}}$ function, where 𝜖 ≈ 10^− 5, which fairly mimics the various properties of the δ distribution at a discrete level. In Fig. 20 a and b, numerical solutions with the FDS scheme are presented, which are in agreement with the time-independent solutions ρ(t,x) = 2δ(x), q(t,x) ≡ 0. Similarly, the authors show that a time-dependent solution can also be constructed on replacing ρ^o by δ(x − 𝜖) + δ(x + 𝜖) and q^o by δ(x − 𝜖) − δ(x + 𝜖) in the above initial conditions. In Fig. 21 a and b, reference solutions are plotted utilizing the exact solutions as given in the above-mentioned article with 200 grid points at t = 0.2 units. From the reference solutions, it is clear that a small perturbation in the initial conditions may lead to large variations in the final solutions. On the other hand, computations with the FDS scheme as given in Figs. 22a, b, 23 a and b generate time-independent numerical solutions with a single beam of delta shocks. Moreover, the FDS scheme retains an almost identically zero numerical product ρu and keeps the numerical velocity at approximately zero level.

Fig. 16

a Numerical results for density variable and b numerical results for u variable with the modified FDS scheme

Fig. 17

a Numerical results for density variable and b numerical results for u variable with a Godunov-type flux [19]

Fig. 18

a Numerical results for density variable and b numerical results for u variable with a Rusanov method [25]

Fig. 19

a Numerical results for density and bu variables respectively with 1280 grid points using a modified FDS-based numerical fluxes for a test case from [28, Eq. 116, pp. 132]

Fig. 20

Numerical results with a modified FDS scheme for a density variable and bρu with 200 grid points at t = 0.3 units for a test case from [2, Example 2.1]

Fig. 21

Reference solutions for a density variable and bu variable with 200 grid points at t = 0.2 units utilizing the exact solutions for a weakly perturbed test case as given in [2, Example 2.1]

Fig. 22

Numerical results with a modified FDS scheme for a density variable and bρu using 200 grid points at t = 0.1 units for a weakly perturbed test case from [2, Example 2.1]

Fig. 23

Numerical results with a modified FDS scheme for u variable using 200 grid points at at = 0.1 units and bt = 0.2 units for a weakly perturbed test case from [2, Example 2.1]

6 2-D pressureless system

In a multi-dimension, the system of presureless gas dynamics can be written as follows:

$$ \frac{\partial \boldsymbol{U}}{\partial{t}} \ + \ {\nabla}\boldsymbol{.H} \ = \ \boldsymbol{0}. $$

Here, U is the vector of conserved variables and H is the flux vector and are given as follows:

$$ \boldsymbol{U} \ = \ \left[\begin{array}{cc} \rho \\[0.4em] \rho u \\[0.4em] \rho v \\[0.4em] \end{array}\right], \ \boldsymbol{H} \ = \ \boldsymbol{F} \hat{i} \ + \ \boldsymbol{G} \hat{j} \ = \ \left[\begin{array}{cc} \rho u \\[0.4em] \rho u^{2} \\[0.4em] \rho uv \\[0.4em] \end{array}\right]\hat{i} \ \ + \ \ \left[\begin{array}{cc} \rho v \\[0.4em] \rho uv \\[0.4em] \rho v^{2} \\[0.4em] \end{array}\right]\hat{j}, $$

where F = (F₁, F₂, F₃)^t = (ρu,ρu², ρuv)^t and G = (G₁, G₂, G₃)^t = (ρv,ρuv,ρv²)^t. The update formula in a finite volume framework for Cartesian geometry can be written as follows:

$$ \boldsymbol{U}_{i,j}^{n+1} \ = \ \boldsymbol{U}_{i,j}^{n} \ - \ \frac{{\Delta}{t}}{{\Delta}{x}} \left[\boldsymbol{F}_{i+\frac{1}{2},j} \ - \ \boldsymbol{F}_{i-\frac{1}{2},j}\right] \ - \ \frac{{\Delta}{t}}{{\Delta}{y}} \left[\boldsymbol{G}_{i,j+\frac{1}{2}} \ - \ \boldsymbol{G}_{i,j-\frac{1}{2}}\right]. $$

On using a similar approach as employed in the 1-D case, both interface fluxes are written as follows:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{F}_{i+\frac{1}{2},j} \ = \ \left\{ \begin{array}{l} 0 \ \ \ \ \text{if} \ \ u_{i,j} < 0 < u_{i+1,j}, \\ \frac{1}{2} \left[\boldsymbol{F}_{i,j} \ + \ \boldsymbol{F}_{i+1,j} \right] \ - \ \frac{1}{2}|\bar u_{i+\frac{1}{2},j}|{\Delta}{\boldsymbol{U}} \ \ \textrm{otherwise,} \end{array} \right. \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \boldsymbol{G}_{i,j+\frac{1}{2}} \ = \ \left\{ \begin{array}{l} 0 \ \ \ \ \text{if} \ \ v_{i,j} < 0 < v_{i,j+1}, \\ \frac{1}{2} \left[\boldsymbol{G}_{i,j} \ + \ \boldsymbol{G}_{i,j+1} \right] \ - \ \frac{1}{2}|\bar v_{i,j+\frac{1}{2}}|{\Delta}{\boldsymbol{U}} \ \ \textrm{otherwise,} \end{array} \right. \end{array} $$

respectively.

6.1 Numerical examples

In this section, some numerical examples are considered [33, Examples 9,11] to check the performance of a modified FDS-based method for vacuum and δ shock-related problems. In the beginning, a test case with the following initial conditions is taken as follows:

$$ \begin{array}{@{}rcl@{}} \rho(x,y,0) \ = \ 0.5 \ , \ \ \ \ (u,v)(x,y,0) \ = \ \left\{ \begin{array}{ll} (0.3,0.4), & \quad x > 0, y > 0, \\ (-0.4,0.3), & \quad x<0,y>0, \\ (-0.3,-0.4), & \quad x<0,y<0, \\ (0.4,-0.3), & \quad x>0, y<0. \end{array} \right. \end{array} $$

For all 2-D computations, CFL = 0.5 is used and the numerical results corresponding to the density variable on coarse and fine grids are shown in Fig. 24 a and b respectively. Similarly, the δ shock capturing property of a modified FDS-based method is demonstrated through the following example as follows:

$$ \begin{array}{@{}rcl@{}} \rho(x,y,0) \ = \ 0.1 \ , \ \ \ \ (u,v)(x,y,0) \ = \ \left\{ \begin{array}{ll} (-0.25,-0.25), & \quad x > 0, y > 0, \\ (0.25,-0.25), & \quad x<0,y>0, \\ (0.25,0.25), & \quad x<0,y<0, \\ (-0.25,0.25), & \quad x>0, y<0. \end{array} \right. \end{array} $$

On comparing Fig. 25 a and b, it is found that the FDS-based method captures δ shocks with almost three times better accuracy than Rusanov method.

Fig. 24

Numerical results for density variable a with 50 × 50 computational cells, ρ ∈ [5.0113 × 10^− 3,0.5] and b with 100 × 100 cells, ρ ∈ [5.0226 × 10^− 5,0.5] in the case of a modified FDS scheme at t = 0.1 units

Fig. 25

Numerical results for density variable a with Rusanov method and b with a modified FDS method using 200 × 200 computational cells at t = 0.5 units

7 Summary

The upwind methods developed in this study are simple to adopt as there is no direct contribution of eigenvectors or generalized eigenvectors in the final formulation of each scheme for the considered systems. In particular, the FDS schemes are free from complicated Riemann solvers, and thus, they can be used to construct higher order weighted essentially non-oscillatory [13, 20] or discontinuous Galerkin [4, 5] schemes without many difficulties. The strategy presented in this work can be further used to investigate more complex systems.