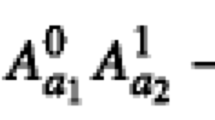Generating tripartite nonlocality from bipartite resources

Abstract

Nonlocality is an important resource for quantum information processing. Tripartite nonlocality is more difficult to produce in experiments than bipartite ones. In this paper, we analyze a simple setting to generate tripartite nonlocality from two classes of bipartite resources, namely two-qubit entangled pure states and Werner states. Upper bounds on the tripartite nonlocality, characterized by the maximal violation of Svetlichny inequalities, are given, and the optimal measurements to achieve these bounds are provided.

1 Introduction

Nonlocality is one of the most fundamental characteristics of quantum mechanics. The nonlocal quantum correlations existing between spatially separated quantum systems have significant advantages over classical correlations, thus serving as an indispensable resource for quantum information processing. In recent years, many novel applications of nonlocality have been developed for quantum computation and quantum communication [1], including communication complexity [2], quantum cryptography [3], randomness generation [4], and device-independent quantum computation [5].

The quantum states which exhibit nonlocal correlations are called nonlocal states. The nonlocality of a quantum state can be verified by Bell-type inequalities which give upper bounds on all local correlations that admit a local hidden variable (LHV) model [1]. For bipartite quantum systems, a sufficient criterion of being nonlocal is the violation of Clauser–Horner–Shimony–Holt (CHSH) inequality [6]. Any purely entangled two-qubit state violates the CHSH inequality [7] while it is not true for mixed states. In 1989, Werner found a class of two-qubit states which are entangled while admit LHV models [8]. In 1995, Horodecki et al. [9] developed a complete characterization for arbitrary two-qubit systems to violate CHSH inequality.

Similarly, for tripartite systems the violation of Svetlichny inequality serves as a sufficient condition of being nonlocal [10]. However, the problem regarding multipartite nonlocality is much more complicated than the bipartite case, and very few works were presented in the literature. Even the nonlocality of three-qubit states, the simplest multipartite systems, is not well understood. In this special case, Ghose et al. derived an analytical expression of nonlocality for the generalized GHZ states and W states [11]. Later in 2010, Ajoy and Rungta [12] extended this result to a set of more general GHZ-class states and W-class states.

In experiments, it is much harder to produce entangled tripartite systems than that of bipartite systems. To overcome this difficulty, Zeilinger et al. [13] proposed a scheme of generating tripartite entanglement from bipartite resources. In the experimental test of nonlocality in GHZ states, the entanglement preparation can also benefit from Zeilinger’s scheme [14]. Note that being entangled is the necessary condition of being nonlocal for quantum systems. Therefore, it has practical meaning to generate tripartite nonlocal systems from bipartite ones.

In this paper, we consider a simple setting to generate tripartite nonlocality from two classes of bipartite resources, namely two-qubit entangled pure states and Werner states. Upper bounds on the tripartite nonlocality, characterized by the maximal violation of Svetlichny inequalities, are given, and the optimal measurements to achieve these bounds are provided.

2 Svetlichny inequalities and their maximal violation

To quantify the nonlocality of three-qubit states, we first review Svetlichny inequalities and then develop a technique of finding the maximal violation of Svetlichny inequalities for a special class of three-qubit (pure or mixed) states. As a by-product, we employ this technique to calculate the nonlocality of generalized tripartite GHZ states.

2.1 Svetlichny inequalities

The nonlocality test scenario for three-qubit systems considered in this paper has two projective measurements each with two outcomes on each party. Without loss of generality, let the two measurement observables for system A are $A = \mathbf {a}\cdot \mathbf {\sigma }$ and $A' = \mathbf {a'}\cdot \mathbf {\sigma }$, where $\mathbf {a}$ and $\mathbf {a'}$ are three-dimensional unit real row vectors, and $\mathbf {\sigma }= (\sigma _{1}, \sigma _{2}, \sigma _{3})$ is the vector of Pauli matrices. Note that each observable is Hermitian operator with eigenvalues $+1$ and $-1$. Similarly, we have $B = \mathbf {b}\cdot \mathbf {\sigma }$ and $B' = \mathbf {b'}\cdot \mathbf {\sigma }$ for system B, and $C = \mathbf {c}\cdot \mathbf {\sigma }$ and $C' = \mathbf {c'}\cdot \mathbf {\sigma }$ for system C, where $\mathbf {b}, \mathbf {b'}, \mathbf {c}, \mathbf {c'} \in {\mathbb {R}}^{3}$ are unit vectors. Then, the Svetlichny operator corresponding to $A, A', B, B', C, C'$ is defined as

$$\begin{aligned} S \equiv (A + A'){\otimes }(B\otimes C' + B'\otimes C) + (A - A')\otimes (B\otimes C - B'\otimes C'). \end{aligned}$$

If a three-qubit state $\rho$ admits a LHV model, then it satisfies the Svetlichny inequality

$$\begin{aligned} tr(S{\rho }) \le 4 \end{aligned}$$

for all possible Svetlichny operators S. Conversely, a three-qubit state which violates this inequality for some S is nonlocal. To quantify the nonlocality of a three-qubit system, we need to compute the maximum of the so-called Svetlichny value

$$\begin{aligned} S_\mathrm{{max}}({\rho }) \equiv \max tr(S{\rho }) \end{aligned}$$

where the maximization is taken over all possible Svetlichny operators. Thus, $S_\mathrm{{max}}(\rho ) > 4$ is a sufficient condition for $\rho$ to be nonlocal. Moreover, Svetlichny inequalities are maximally violated by the GHZ state $(|000\rangle + |111\rangle )/\sqrt{2}$ with the maximal Svetlichny value being $4\sqrt{2}$ [10].

2.2 Maximal violation of Svetlichny inequalities for general three-qubit states

Recall that any three-qubit state $\rho$ can be expressed under the Pauli basis as

$$\begin{aligned} \rho = \frac{1}{8} \sum \limits _{i,j,k=0}^{3}t_{ijk} \sigma _{i} \otimes \sigma _{j} \otimes \sigma _{k} \end{aligned}$$

where $t_{ijk} = tr(\rho \sigma _{i} \otimes \sigma _{j} \otimes \sigma _{k}) \in {\mathbb {R}}$. For any measurement observables $A = \mathbf {a}\cdot \mathbf {\sigma }$, $B = \mathbf {b}\cdot \mathbf {\sigma }$, and $C = \mathbf {c}\cdot \mathbf {\sigma }$, the expectation of the product of the measurement outcomes of $\rho$ is

$$\begin{aligned} tr\left[ \rho \left( A \otimes B \otimes C\right) \right]= & {} \sum _{i,j,k=1}^{3}a_{i}t_{ijk}b_{j}c_{k} = \langle \mathbf {a}, T_{c}\mathbf {b}\rangle \end{aligned}$$

where $T_{c} \equiv \sum _{k=1}^{3} c_{k} T_{k}$, and for each k, the Pauli coefficients matrix $T_{k} = (t_{ijk})$ is a 3 by 3 real matrix indexed by i and j. Here $\langle \cdot , \cdot \rangle$ denotes the normal inner product in ${\mathbb {R}}^{3}$, and we abuse the notation slightly by writing $T_{c}\mathbf {b}$ for $T_{c}\mathbf {b}^T$.

Let $\mathbf {e}$ and $\mathbf {e'}$ be two orthogonal unit vectors such that $\mathbf {a} + \mathbf {a'} = 2 \cos {\alpha } \mathbf {e}$ and $\mathbf {a} - \mathbf {a'} = 2 \sin {\alpha } \mathbf {e'}$ for some $\alpha$. Let $E \equiv \mathbf {e}\cdot \mathbf {\sigma }$ and $E' \equiv \mathbf {e'}\cdot \mathbf {\sigma }$. Then,

$$\begin{aligned} S(\rho )&= 2 \cos {\alpha }\; tr(E\otimes (B\otimes C' + B'\otimes C)\rho ) \nonumber \\&\quad +\ 2 \sin {\alpha }\; tr(E'\otimes (B\otimes C - B'\otimes C')\rho ) \nonumber \\&= 2 \cos {\alpha } \langle \mathbf {e}, \mathbf {\lambda _{0}}\rangle + 2 \sin {\alpha } \langle \mathbf {e'}, \mathbf {\lambda _{1}}\rangle \\&\overset{(a)}{\le } 2\sqrt{\langle \mathbf {e}, \mathbf {\lambda _{0}}\rangle ^{2} + \langle \mathbf {e'}, \mathbf {\lambda _{1}}\rangle ^{2}} \nonumber \\&\le 2\sqrt{\Vert \mathbf {\lambda _{0}} \Vert ^{2} + \Vert \mathbf {\lambda _{1}} \Vert ^{2}},\nonumber \end{aligned}$$

(1)

where

$$\begin{aligned} \mathbf {\lambda _{0}}\equiv & {} T_{c'} \mathbf {b} + T_{c}\mathbf {b'} \end{aligned}$$

(2)

$$\begin{aligned} \mathbf {\lambda _{1}}\equiv & {} T_{c}\mathbf {b} - T_{c'}\mathbf {b'}. \end{aligned}$$

(3)

Here the inequality (a) comes from the Cauchy–Schwarz inequality. The following lemma plays a crucial role in our later discussion.

Lemma 1

Let $\rho$ be a three-qubit state with the Pauli coefficients matrices $T_{k}$, $k=1, 2, 3$. Then,

$$\begin{aligned} S_\mathrm{{max}}(\rho ) \le \max _{\mathbf {b},\mathbf {b'},\mathbf {c},\mathbf {c'}}2 \sqrt{\Vert \mathbf {\lambda _{0}} \Vert ^{2} + \Vert \mathbf {\lambda _{1}} \Vert ^{2}} \end{aligned}$$

(4)

where $\mathbf {\lambda _{0}}$ and $\mathbf {\lambda _{1}}$ are defined in Eqs.(2) and (3). Furthermore, if the maximum on the right-hand side of Eq.(4) can be obtained for some $\mathbf {\lambda _{0}}$ and $\mathbf {\lambda _{1}}$ with $\mathbf {\lambda _{0}}\perp \mathbf {\lambda _{1}}$, then the equality holds.

Proof

The upper bound has been proved in Eq.(1). Suppose there are unit vectors $\mathbf {b}$, $\mathbf {b'}$, $\mathbf {c}$, and $\mathbf {c'}$ which achieve the maximum on the right-hand side of Eq.(4) and make $\mathbf {\lambda _{0}}\perp \mathbf {\lambda _{1}}$. Without loss of generality, we can assume that both $\mathbf {\lambda _{0}}$ and $\mathbf {\lambda _{1}}$ are nonzero; otherwise, the result holds trivially. Let $\mathbf {e} = \mathbf {\lambda _{0}}/\Vert \mathbf {\lambda _{0}}\Vert$, $\mathbf {e'} = \mathbf {\lambda _{1}}/\Vert \mathbf {\lambda _{1}}\Vert$, and $\alpha$ such that the equality holds in (a). Then, the equality in Eq.(4) holds by putting $\mathbf {a}= \cos \alpha \mathbf {e} + \sin \alpha \mathbf {e'}$ and $\mathbf {a'}= \cos \alpha \mathbf {e} - \sin \alpha \mathbf {e'}$. $\square$

In the following subsection, we will use Lemma 1 to calculate the maximal Svetlichny value of the generalized GHZ states. Application of Lemma 1 to a class of mixed three-qubit systems will be shown in Sect. 3.1.

2.3 Nonlocality of generalized GHZ states

The Pauli coefficients matrices of the generalized GHZ states

$$\begin{aligned} |G_{\theta }\rangle = \cos {\theta } |000\rangle + \sin {\theta }|111\rangle \end{aligned}$$

are $T_{k} = \sin {2\theta } T_{k}'$, $k=1,2,3$, where

$$\begin{aligned} T'_{1}= & {} \left( \begin{array}{ccc} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{array} \right) , \\ T'_{2}= & {} \left( \begin{array}{ccc} 0 &{}\quad -1 &{}\quad 0 \\ -1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{array} \right) , \\ T'_{3}= & {} \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \cot {2\theta }\end{array} \right) . \end{aligned}$$

Suppose $\mathbf {b} = (\sin {\beta }\sin {\eta }, \sin {\beta }\cos {\eta }, \cos {\beta }), \mathbf {b'} = (\sin {\beta '}\sin {\eta '}, \sin {\beta '}\cos {\eta '}, \cos {\beta '}), \mathbf {c} = (\sin {\gamma }\sin {\varphi }, \sin {\gamma }\cos {\varphi }, \cos {\gamma })$ and $\mathbf {c'} = (\sin {\gamma '}\sin {\varphi '}, \sin {\gamma '}\cos {\varphi '}, \cos {\gamma '})$. Then, the vectors $\mathbf {\lambda _{0}'}$ and $\mathbf {\lambda _{1}'}$ corresponding to these parameters are

$$\begin{aligned} \mathbf {\lambda _{0}'}= & {} \left( \begin{array}{c} -\sin {\beta '} \sin {\gamma } \cos {(\eta ' + \varphi )} - \sin {\beta } \sin {\gamma '} \cos {(\eta + \varphi ')} \\ -\sin {\beta '} \sin {\gamma } \sin {(\eta ' + \varphi )} - \sin {\beta } \sin {\gamma '} \sin {(\eta + \varphi ')} \\ \cot {2\theta }(\cos {\beta '} \cos {\gamma } + \cos {\beta } \cos {\gamma '} ) \end{array} \right) \\ \mathbf {\lambda _{1}'}= & {} \left( \begin{array}{c} -\sin {\beta } \sin {\gamma } \cos {(\eta + \varphi )} + \sin {\beta '} \sin {\gamma '} \cos {(\eta ' + \varphi ')} \\ -\sin {\beta } \sin {\gamma } \sin {(\eta + \varphi )} + \sin {\beta '} \sin {\gamma '} \sin {(\eta ' + \varphi ')} \\ \cot {2\theta }(\cos {\beta } \cos {\gamma } - \cos {\beta '} \cos {\gamma '} ) \end{array} \right) \end{aligned}$$

respectively. We further calculate

$$\begin{aligned}&\Vert \mathbf {\lambda _{0}'} \Vert ^{2} + \Vert \mathbf {\lambda _{1}'} \Vert ^{2} \\&\quad = \ \cot ^{2}{2\theta } (\cos ^{2}{\beta } + \cos ^{2}{\beta '})(\cos ^{2}{\gamma } + \cos ^{2}{\gamma '}) \\&\qquad + 4\sin {\beta }\sin {\beta '}\sin {\gamma }\sin {\gamma '} \sin {(\eta - \eta ')} \sin {(\varphi - \varphi ')} \\&\qquad + (\sin ^{2}{\beta } + \sin ^{2}{\beta '})(\sin ^{2}{\gamma } + \sin ^{2}{\gamma '}) \\&\quad \le \ \cot ^{2}{2\theta } (\cos ^{2}{\beta } + \cos ^{2}{\beta '})(\cos ^{2}{\gamma } + \cos ^{2}{\gamma '}) \\&\qquad + 4|\sin {\beta }\sin {\beta '}\sin {\gamma }\sin {\gamma '}| + (\sin ^{2}{\beta }\\&\qquad + \sin ^{2}{\beta '})(\sin ^{2}{\gamma } + \sin ^{2}{\gamma '}) \\&\quad \le \ \cot ^{2}{2\theta } (\cos ^{2}{\beta } + \cos ^{2}{\beta '})(\cos ^{2}{\gamma } + \cos ^{2}{\gamma '})\\&\qquad + 2(\sin ^{2}{\beta } + \sin ^{2}{\beta '})(\sin ^{2}{\gamma } + \sin ^{2}{\gamma '}), \end{aligned}$$

where the last inequality is from the fact that

$$\begin{aligned} 4\sin {\beta }\sin {\beta '}\sin {\gamma }\sin {\gamma '} \le (\sin ^{2}{\beta } + \sin ^{2}{\beta '})(\sin ^{2}{\gamma } + \sin ^{2}{\gamma '}) \end{aligned}$$

for any $\beta , \beta ', \gamma$, and $\gamma '$. Let $x \equiv \sin ^{2}{\beta } + \sin ^{2}{\beta '}$ and $y \equiv \sin ^{2}{\gamma } + \sin ^{2}{\gamma '}$. Then,

$$\begin{aligned}&\Vert \mathbf {\lambda _{0}'} \Vert ^{2} + \Vert \mathbf {\lambda _{1}'} \Vert ^{2} \\&\le (2 + \cot ^{2}{2\theta })xy - 2\cot ^{2}{2\theta }(x + y) + 4\cot ^{2}{2\theta } \\&\equiv f(x,y). \end{aligned}$$

Note that the function f(x, y) is symmetric with respect to x and y, and if $x<y$, then $f(x+\epsilon , y -\epsilon ) > f(x, y)$ whenever $0< \epsilon < y-x$. Thus, f(x, y) reaches its maximum at some point with $x=y$. Inserting $x=y$ into the formula, and noting that $x,y\in [0,2]$, we have

$$\begin{aligned} f(x,y) \le \left\{ \begin{array}{lll} 8&{} \text { if } \cot ^{2}{2\theta } \le 2 \\ 4\cot ^{2}{2\theta }&{} \text { if } \cot ^{2}{2\theta } > 2, \end{array} \right. \end{aligned}$$

where for the above case, the equality holds when $x=y=2$, while for the below one, it holds when $x=y=0$.

When $\cot ^{2}{2\theta } \le 2$, a simple calculation shows that the maximum of $\Vert \mathbf {\lambda _{0}'} \Vert ^{2} + \Vert \mathbf {\lambda _{1}'} \Vert ^{2}$ can be achieved by taking $\beta = \beta ' = \gamma = \gamma ' = \eta = \varphi = \pi /2$ while $\eta ' = \varphi ' =0$. In this case, $\mathbf {\lambda _{0}'} = (0, -2, 0)$ and $\mathbf {\lambda _{1}' }= (2, 0, 0)$. Thus, $\mathbf {\lambda _{0}'} \perp \mathbf {\lambda _{1}'}$, and by Lemma 1, we derive $S_\mathrm{{max}}(G_{\theta }) = 4\sqrt{2}|\sin {2\theta }|$.

When $\cot ^{2}{2\theta } > 2$, the maximum of $\Vert \mathbf {\lambda _{0}'} \Vert ^{2} + \Vert \mathbf {\lambda _{1}'} \Vert ^{2}$ can be achieved by taking $\beta = \beta ' = \gamma = \gamma ' = 0$ while other parameters arbitrarily. In this case, $\mathbf {\lambda _{0}'} = (0, 0, 2\cot 2\theta )$ and $\mathbf {\lambda _{1}' }= (0, 0, 0)$. Thus, $\mathbf {\lambda _{0}'} \perp \mathbf {\lambda _{1}'}$, and by Lemma 1, we derive $S_\mathrm{{max}}(G_{\theta }) = 4|\cos {2\theta }|$.

Note that the condition $\cot ^{2}{2\theta } > 2$ is equivalent to $\sin ^{2}{2\theta } < \frac{1}{3}$. Therefore, the maximal violation of Svetlichny inequalities for the generalized GHZ states is

$$\begin{aligned} S_\mathrm{{max}}(G_{\theta }) = \left\{ \begin{array}{ll} 4|\cos {2\theta }|&{} \text { if } \sin ^{2}{2\theta } < \frac{1}{3} \\ 4\sqrt{2}|\sin {2\theta }| &{} \text { if } \sin ^{2}{2\theta } \ge \frac{1}{3}, \end{array} \right. \end{aligned}$$

which coincides the result obtained by Ghose et al. [11].

3 Generating tripartite nonlocality from bipartite resource

We analyze in this paper a simple setting, shown in Fig. 1, for generating tripartite nonlocality from bipartite resources. Suppose there are three remotely located participants Alice, Bob, and Clare. Alice and Bob each shares a copy of the resource state $\rho$ with Clare, denoted as $\rho _{AC_{1}}$ and $\rho _{BC_{2}}$, respectively.

Clare then applies a CNOT operation on $C_{1}$ (the control qubit) and $C_{2}$ (the target qubit) and measures the system $C_{2}$ with some projective measurement. The tripartite nonlocality of the remaining systems $ABC_1$ will be quantified by the maximal violation of Svetlichny inequalities.

Fig. 1

Setting for tripartite nonlocality generation

In the following subsections, two different types of resource states are investigated: two-qubit Werner states

$$\begin{aligned} \rho _{W} = p|\Phi \rangle \langle \Phi | + (1-p) \frac{I}{4} \end{aligned}$$

(5)

where $0< p < 1$ and $|\Phi \rangle =(|00\rangle + |11\rangle )/\sqrt{2}$, and arbitrarily entangled two-qubit pure states with the Schmidt decomposition

$$\begin{aligned} |\Phi _{\theta }\rangle = \cos {\theta } |00\rangle + \sin {\theta }|11\rangle , \quad 0<\theta < \frac{\pi }{2}. \end{aligned}$$

(6)

3.1 Werner states as the resource

Werner states are an important class of quantum states which show that, rather surprisingly, not all entangled states are nonlocal. This indicates that entanglement and nonlocality are different resources. In this subsection, we consider two-qubit Werner states as the resource in our setting and analyze the nonlocality of post-measurement states.

Suppose the projective measurement applied by Clare on system $C_{2}$ is in the following orthonormal basis

$$\begin{aligned} |\psi _{0}\rangle= & {} \sin \tau |0\rangle + \cos \tau |1\rangle \end{aligned}$$

(7)

$$\begin{aligned} |\psi _{1}\rangle= & {} \cos \tau |0\rangle - \sin \tau |1\rangle . \end{aligned}$$

(8)

If the system is projected to $|\psi _{0}\rangle$, the post-measurement state of $ABC_1$ will be

$$\begin{aligned} \rho _{0} = 2\ tr_{C_{2}}\left( \rho | \psi _{0}\rangle \langle \psi _{0} |\right) \end{aligned}$$

where $\rho = {\text{ CNOT }}_{C_1C_2}(\rho _{W}\otimes \rho _{W})$. The Pauli coefficients matrices of $\rho _{0}$ are $p^2 T_{k}$, $k=1,2,3$, where

$$\begin{aligned} T_{1}= & {} \left( \begin{array}{ccc} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \sin {2\tau } \end{array} \right) ,\\ T_{2}= & {} \left( \begin{array}{ccc} 0 &{}\quad \cos {2\tau } &{}\quad 0 \\ \cos {2\tau } &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{array} \right) \end{aligned}$$

and $T_{3} = 0$. A routine calculation shows that

$$\begin{aligned}&\Vert \mathbf {\lambda _{0}} \Vert ^{2} + \Vert \mathbf {\lambda _{1}} \Vert ^{2} \\&= \cos ^{2}{2\tau }\left( b_{1}^{2} + b_{2}^{2} + {b_{1}'}^{2} + {b_{2}'}^{2}\right) \left( c_{1}^{2} + c_{2}^{2} + {c_{1}'}^{2} + {c_{2}'}\right) \\&+ 2\sin ^{2}{2\tau }\left( c_{1}^{2} + {c_{1}'}^{2}\right) + 4\cos {2\tau }\left( b_{1}'b_{2} - b_{1}b'_{2}\right) \left( c_{1}c_{2}' - c_{1}'c_{2}\right) . \end{aligned}$$

Note that the above formula is a homogeneous polynomial of degree 2, and it does not depend on $b_3, b_3', c_3$, and $c_3'$. Thus, the maximum of the formula must be obtained at some point where $b_3=b_3'=c_3=c_3'=0$. Then,

$$\begin{aligned}&\max _{\mathbf {b}, \mathbf {b}', \mathbf {c}, \mathbf {c}'} (\Vert \mathbf {\lambda _{0}} \Vert ^{2} + \Vert \mathbf {\lambda _{1}} \Vert ^{2}) = 4\cos ^{2}{2\tau } + 2 \max _{\mathbf {b}, \mathbf {b}', \mathbf {c}, \mathbf {c}'} F(\mathbf {\lambda _{0}}, \mathbf {\lambda _{1}}) \end{aligned}$$

where

$$\begin{aligned} F(\mathbf {\lambda _{0}}, \mathbf {\lambda _{1}}) \equiv \sin ^{2}{2\tau }\left( c_{1}^{2} + {c_{1}'}^{2}\right) + 2\cos {2\tau }\left( b_{1}'b_{2} - b_{1}b'_{2}\right) \left( c_{1}c_{2}' - c_{1}'c_{2}\right) . \end{aligned}$$

To further optimize $F(\mathbf {\lambda _{0}}, \mathbf {\lambda _{1}})$, we need the following lemma.

Lemma 2

For any $x, y\ge 0$ and $\alpha , \beta \in {\mathbb {R}}$,

$$\begin{aligned} x(\cos ^{2}\alpha - \sin ^{2}\beta ) + y\sin (\alpha - \beta ) \le \sqrt{x^{2} + y^{2}}, \end{aligned}$$

and the equality holds if and only if $|\cos {2\alpha }| = \frac{x}{\sqrt{x^{2} + y^{2}}}$ and $\alpha + \beta = k\pi$ for some integer k.

Proof

Note that

$$\begin{aligned} \cos ^{2}\alpha - \sin ^{2}\beta = \cos (\alpha + \beta ) \cos (\alpha - \beta ). \end{aligned}$$

The result is then easy from the Cauchy–Schwarz inequality. $\square$

Let $c_{1} =\cos {\alpha }, c_{2} =\sin {\alpha }, c_{1}' = \cos {\beta }$, and $c_{2}' = \sin {\beta }$. Then,

$$\begin{aligned}&F(\mathbf {\lambda _{0}}, \mathbf {\lambda _{1}}) \\&\le \sin ^{2}{2\tau }(\cos ^{2}\alpha + \cos ^{2}\beta ) + 2|\cos {2\tau }| \cdot |\sin (\alpha - \beta )| \\&\le \sin ^{2}{2\tau } + \sqrt{\sin ^{4}{2\tau } + 4\cos ^{2}{2\tau }} \\&= 2 \end{aligned}$$

where the first equality is from the fact that $b_{1}'b_{2} - b_{1}b'_{2} \le 1$ which is in turn from the Cauchy–Schwarz inequality, and the second equality comes from Lemma 2. Furthermore, it is easy to check that the upper bound is achievable by taking, say,

$$\begin{aligned} c_1&= c_1' = \frac{1}{\sqrt{1+\cos ^2 2\tau }}, \\ -c_2&= c_2' = \frac{\cos 2\tau }{\sqrt{1+\cos ^2 2\tau }}, \\ b_1&= -b_2' = 1,\\ b_2&= b_1' = 0. \end{aligned}$$

In this case, we have

$$\begin{aligned} \mathbf {\lambda _{0}}= & {} \sqrt{1 + \cos ^{2}{2\tau }}\ (1, 1, 0), \\ \mathbf {\lambda _{1}}= & {} \sqrt{1 + \cos ^{2}{2\tau }}\ (1, -1, 0). \end{aligned}$$

Thus, $\mathbf {\lambda _{0}} \perp \mathbf {\lambda _{1}}$, and by Lemma 1,

$$\begin{aligned} S_\mathrm{{max}}(\rho _{0}) = 4p^{2}\sqrt{1 + \cos ^{2}{2\tau }}. \end{aligned}$$

By a similar calculation, we can show that $S_\mathrm{{max}}(\rho _{1}) = 4p^{2}\sqrt{1 + \cos ^{2}{2\tau }}$ as well, where $\rho _{1}$ is the post-measurement state of $ABC_1$ when the system $C_{2}$ is projected to $|\psi _{1}\rangle$.

If we choose $\cos {\tau } = 0$ or $\cos {\tau } = \pm 1$, which corresponds to the projective measurement in the standard basis on system $C_{2}$, the maximal value $4p^{2}\sqrt{2}$ is achieved for both $\rho _0$ and $\rho _1$. With this, we have proved the following theorem which is the main result of this subsection.

Theorem 1

Let $\rho$ in Fig. 1 be a Werner state defined in Eq.(5), and Clare is only allowed to perform projective measurement in the $X-Z$ plane. Then, the maximal Svetlichny inequality violation of the remaining states satisfies

$$\begin{aligned} p_{0}S_\mathrm{{max}}(\rho _{0}) + p_{1}S_\mathrm{{max}}(\rho _{1}) \le 4p^{2}\sqrt{2}, \end{aligned}$$

where $\rho _{0}$ and $\rho _1$ are the post-measurement states of system $ABC_{1}$ with the corresponding probabilities $p_{0}$ and $p_{1}$, respectively. The equality holds when the measurement in the standard basis $\{ |0\rangle , |1\rangle \}$ is applied. Furthermore, in this case the maximal violation $4p^{2}\sqrt{2}$ is achieved for both measurement outcomes; thus, tripartite nonlocality is generated with certainty if $p > 2^{-\frac{1}{4}} \approx 0.8409$.

3.2 Two-qubit pure states as the resource

Now we turn to the case where an arbitrary two-qubit pure state $|\Phi _{\theta }\rangle$ described in Eq.(6) serves as the resource in our setting. By applying the CNOT operation, the initial state $|\Phi _{\theta }\rangle _{AC_{1}}|\Phi _{\theta }\rangle _{BC_{2}}$ will be transformed to

$$\begin{aligned}&|\psi \rangle _{ABC_{1}C_{2}} \\&= \cos ^{2}{\theta } |0000\rangle + \sin ^{2}{\theta } |1110\rangle + \sin {\theta }\cos {\theta } (|0101\rangle +|1011\rangle ) \nonumber \\&\equiv x_0 |\Phi _{0}\rangle |0\rangle + x_1 |\Phi _{1}\rangle |1\rangle \end{aligned}$$

where $x_{0}=\sqrt{\cos ^{4}{\theta } + \sin ^{4}{\theta }}$, $x_{1}=\sqrt{2}\cos {\theta }\sin {\theta }$, and

$$\begin{aligned} |\Phi _{0}\rangle= & {} \alpha _{0}|000\rangle + \alpha _{1}|111\rangle \end{aligned}$$

(9)

$$\begin{aligned} |\Phi _{1}\rangle= & {} ( |010\rangle + |101\rangle )/\sqrt{2} \end{aligned}$$

(10)

with $\alpha _{0} =\frac{\cos ^{2}{\theta }}{x_0}$ and $\alpha _{1} =\frac{\sin ^{2}{\theta }}{x_0}$.

Suppose Clare measures the system $C_{2}$ according to the following orthonormal basis

$$\begin{aligned} |\varphi _{0}\rangle= & {} \mu _{0} |0\rangle + \mu _{1} |1\rangle \\ |\varphi _{1}\rangle= & {} \mu _{1} |0\rangle - \mu _{0} |1\rangle \end{aligned}$$

where $\mu _{0}, \mu _{1}\in {\mathbb {R}}$ and $\mu _{0}^{2} + \mu _{1}^{2}=1$. The probability of projecting system $C_{2}$ into the state $|\varphi _{0}\rangle$ is $p_{0} = \mu _{0}^{2} x_{0}^{2} + \mu _{1}^{2} x_{1}^{2}$, and the post-measurement state of system $ABC_{1}$ is

$$\begin{aligned} |\Psi _{0}\rangle = \left( \mu _{0}x_{0} |\Phi _{0}\rangle + \mu _{1} x_{1} |\Phi _{1}\rangle \right) /\sqrt{p_{0}}. \end{aligned}$$

(11)

The measurement projects system $C_{2}$ into $|\varphi _{1}\rangle$ with probability $p_{1} = 1 - p_{0}$ and the state of $ABC_{1}$ becomes

$$\begin{aligned} |\Psi _{1}\rangle = (\mu _{1}x_{0} |\Phi _{0}\rangle - \mu _{0} x_{1} |\Phi _{1}\rangle )/\sqrt{p_{1}}. \end{aligned}$$

(12)

To evaluate the nonlocality of the states in Eqs.(11) and (12), we need a lemma.

Lemma 3

Let $|\Psi \rangle _{ABC} \equiv \omega _{0} |\Phi _{0}\rangle + \omega _{1} |\Phi _{1}\rangle$ where $|\Phi _{0}\rangle$ and $|\Phi _{1}\rangle$ are defined in Eqs.(9) and (10), respectively, $\omega _{0}, \omega _{1}\in {\mathbb {R}}$, and $\omega _{0}^{2} + \omega _{1}^{2} = 1$. Then,

$$\begin{aligned} S_\mathrm{{max}}(\Psi ) \le 4\sqrt{2 + 4 \alpha _{0}\alpha _{1}\left( 1+2\alpha _{0}\alpha _{1}\right) \left( \omega _{0}^{4} - \frac{1}{2\alpha _{0}\alpha _{1}}\omega _{0}^{2}\right) } \end{aligned}$$

and the equality holds when

$$\begin{aligned} 12\left( \omega _{0}^{2}\alpha _{0}\alpha _{1} - \frac{\omega _{1}^{2}}{2}\right) ^{2} + 2\omega _{0}^{2} \omega _{1}^{2} (\alpha _{0} + \alpha _{1})^{2} \ge 1. \end{aligned}$$

(13)

Proof

By reordering the systems ABC, the state $|\Psi \rangle$ can be rewritten as

$$\begin{aligned} |\Psi \rangle _{ACB} =\ |00\rangle (\omega _{0}\alpha _{0} |0\rangle + \frac{\omega _{1}}{\sqrt{2}} |1\rangle ) + |11\rangle \left( \frac{\omega _{1}}{\sqrt{2}} |0\rangle + \omega _{0}\alpha _{1} |1\rangle \right) . \end{aligned}$$

Let

$$\begin{aligned} U = \frac{\omega _0\alpha _0}{\sqrt{r}} \sigma _3 + \frac{\omega _{1}}{\sqrt{2r}} \sigma _1 \end{aligned}$$

be a unitary operator, where $\sigma _1$ and $\sigma _3$ are Pauli matrices and $r= \omega _{0}^{2}\alpha _{0}^{2} + \frac{\omega _{1}^{2}}{2}$. Then,

$$\begin{aligned} (I_{AC}\otimes U_B) |\Psi \rangle _{ACB} = \sqrt{r} |00\rangle |0\rangle + \sqrt{1-r} |11\rangle |\phi \rangle \end{aligned}$$

where

$$\begin{aligned} |\phi \rangle = \frac{\sqrt{2}\omega _{0}\omega _{1}\left( \alpha _{0} + \alpha _{1}\right) |0\rangle + \left( \omega _{1}^{2}- 2\omega _{0}^{2} \alpha _{0}\alpha _{1}\right) |1\rangle }{2\sqrt{r(1-r)}}. \end{aligned}$$

Note that local unitary operations do not affect nonlocality. Then, the lemma holds from [12]. $\square$

With Lemma 3, we calculate the quadratic mean¹ of the maximal Svetlichny violations as

$$\begin{aligned}&\sqrt{p_{0} S_\mathrm{{max}}(\Psi _{0})^{2} + p_{1} S_\mathrm{{max}}(\Psi _{1})^{2}} \nonumber \\&\le 4\sqrt{2 + 4\alpha _{0}\alpha _{1}(2\alpha _{0}\alpha _{1} + 1)\left[ x_{0}^{4}\left( \frac{\mu _{0}^{4}}{p_{0}} + \frac{\mu _{1}^{4}}{p_{1}}\right) - \frac{x_{0}^{2}}{2\alpha _{0}\alpha _{1}}\right] }\\&\le 4\sqrt{2 + 2(4\alpha _{0}^{2}\alpha _{1}^{2} -1)x_{0}^{2}}\ =\ 4 \sqrt{\frac{2\sin ^{2}{2\theta }}{1 + \cos ^{2}{2\theta }}}, \end{aligned}$$

where the second inequality comes from the fact that

$$\begin{aligned} \frac{\mu _{0}^{4}}{p_{0}} + \frac{\mu _{1}^{4}}{p_{1}}&= \frac{1}{x^2}\left[ \frac{\mu _{0}^2}{1+\left( \frac{\mu _1x_1}{\mu _0x_0}\right) ^2} + \frac{\mu _{1}^2}{1+\left( \frac{\mu _0x_1}{\mu _1x_1}\right) ^2}\right] \nonumber \\&\le \frac{1}{x^2}\left( \mu _{0}^2 + \mu _{1}^2\right) = \frac{1}{x^2}. \nonumber \end{aligned}$$

The equality holds when $\mu _{0}^{2} = 0$ or $\mu _{0}^{2} = 1$, which correspond to the projective measurement in the standard basis $\{|0\rangle , |1\rangle \}$. In this case, the post-measurement states $|\Psi _{0}\rangle$ and $|\Psi _{1}\rangle$ are exactly $|\Phi _{0}\rangle$ and $|\Phi _{1}\rangle$ defined in Eqs.(9) and (10), respectively. If $0.4911 \approx \sqrt{\frac{1}{2} - \frac{1}{2} \sqrt{2 - \sqrt{3}}}\le \cos {\theta } \le \sqrt{\frac{1}{2} + \frac{1}{2} \sqrt{2 - \sqrt{3}}} \approx 0.8711$, then Eq.(13) holds for both $|\Psi _{0}\rangle$ and $|\Psi _{1}\rangle$, and the upper bound $4 \sqrt{\frac{2\sin ^{2}{2\theta }}{1 + \cos ^{2}{2\theta }}}$ is obtained.

We summarize our main result in this section as the following theorem.

Theorem 2

Let $\rho = |\Phi _{\theta }\rangle \langle \Phi _{\theta }|$ in Fig. 1 where $|\Phi _{\theta }\rangle$ is defined in Eq.(6) with $0.4911 \le \cos {\theta } \le 0.8711$, and Clare is only allowed to perform projective measurement in the $X-Z$ plane. Then, the quadratic mean of the maximal Svetlichny inequality violations of the remaining states satisfies

$$\begin{aligned} \sqrt{p_{0}S_\mathrm{{max}}(\Psi _{0})^{2} + p_{1}S_\mathrm{{max}}(\Psi _{1})^{2}} \le 4 \sqrt{\frac{2\sin ^{2}{2\theta }}{1 + \cos ^{2}{2\theta }}}, \end{aligned}$$

where $|\Psi _{0}\rangle$ and $|\Psi _{1}\rangle$ are the post-measurement states of system $ABC_{1}$ with the corresponding probabilities $p_{0}$ and $p_{1}$, respectively. The equality holds when the measurement in the standard basis $\{ |0\rangle , |1\rangle \}$ is applied. Furthermore, in this case we have $S_\mathrm{{max}}(\Psi _{1}) = 4\sqrt{2}$ and

$$\begin{aligned} S_\mathrm{{max}}(\Psi _{0}) = \frac{4 \sqrt{2} \sin ^{2}{2\theta }}{1 + \cos ^{2}{2\theta }}. \end{aligned}$$

(14)

Thus, tripartite nonlocality is generated with certainty if

$$\begin{aligned} 0.5412 \approx \sqrt{\frac{2-\sqrt{2}}{2}}< \cos {\theta } < \sqrt{\frac{\sqrt{2}}{2}} \approx 0.8409. \end{aligned}$$

4 Conclusion and future work

In this paper, we investigate a setting of generating tripartite nonlocality from two classes of bipartite resources, namely Werner states and two-qubit pure states. Interestingly, we find in both cases projective measurement according to the standard basis $\{ |0\rangle , |1\rangle \}$ achieves the maximal Svetlichny inequality violation of the remaining states (although the criteria are slightly different).

The setting considered in this paper is, however, still very simple: only a CNOT operation on $C_{1}$ and $C_{2}$ followed by a projective measurement on $C_{2}$ is allowed. For future work, we are going to further exploit the power of the technique we proposed in this paper to derive the maximal Svetlichny violation for other classes of three-qubit states. With this, we will be able to include more general measurements and resources in our setting than those considered in the current paper. More complicated protocols other than the CNOT measurement one can also be examined, which hopefully will extend the capability of our setting to generate tripartite nonlocality.