Quantum pattern recognition with multi-neuron interactions

Abstract

We present a quantum neural network with multi-neuron interactions for pattern recognition tasks by a combination of extended classic Hopfield network and adiabatic quantum computation. This scheme can be used as an associative memory to retrieve partial patterns with any number of unknown bits. Also, we propose a preprocessing approach to classifying the pattern space S to suppress spurious patterns. The results of pattern clustering show that for pattern association, the number of weights ($\eta$) should equal the numbers of unknown bits in the input pattern (d). It is also remarkable that associative memory function depends on the location of unknown bits apart from the d and load parameter $\alpha$.

Adiabatic condition of QNN

The behavior of the QNN depends on runtime AQC. Here, we calculate numerically runtime of the algorithm with high probability in two broad case. Previously, the runtime of AQC for the two-qubit neural network [30] has been calculated analytically for recalling pattern process and pattern association separately in more details [31].

1.1 Runtime of AQC for pattern recalling process

Let us consider Hamiltonian (19) belong to Sect. 4.1 for recalling patterns from the memory of QNN. To do this work, the time-dependent Hamiltonian (8) by defining a dimensionless quantities $s=\frac{t}{T}$ can be written as

$$\begin{aligned} H(t)=(1-s)\frac{1}{2}\sum _{i=1}^4(I-\sigma _i^x)\,+\,s\left( -J(\sigma ^z\otimes \sigma ^z\otimes \sigma ^z\otimes \sigma ^z)+\Gamma \sum _{i=1}^4 \xi _{i}^{\mathrm{inp}} \sigma _{i}^z\right) . \end{aligned}$$

(23)

As an instance, suppose the patterns into the first cluster ($S_1$) with $J=1$ load in the memory and the input pattern ($\xi ^{\mathrm{inp}}$) and $\Gamma$ are $(1,1,1,1)^t$ and 1 / 2 respectively so as H(t) would be

$$\begin{aligned} H(t)=(1-s)\frac{1}{2}\sum _{i=1}^4(I-\sigma _i^x)+s\left( -(\sigma ^z\otimes \sigma ^z\otimes \sigma ^z\otimes \sigma ^z)+\frac{1}{2}(\sigma _{1}^z+\sigma _{2}^z+\sigma _{3}^z+\sigma _{4}^z)\right) . \end{aligned}$$

(24)

Fig. 4

Eigenvalues of the time-dependent Hamiltonian H(s) as a function of the reduced time s for $N=4$ (With the convention $\hbar =1$, the energy as well as the reduced time are dimensionless quantities)

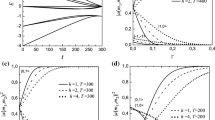
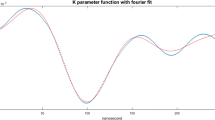
The eigenvalues and eigenstates of H(t) may be achieved analytically, but here we only focus on calculation of $g_{\min }$ and $D_{\max }$ numerically. Therefore, we draw all eigenvalues of H(t) in Fig. 4 and find two lowest eigenvalues of H(t). Then, we define two quantity $g(s)=E_1(s)-E_0(s)$ and $D(s)=\langle E_1|\frac{\mathrm{d}H(s)}{\mathrm{d}t}|E_0\rangle =\frac{1}{T}\langle E_1|\frac{\mathrm{d}H(s)}{\mathrm{d}s}|E_0\rangle$ to calculate adiabatic condition (11). The minimum of g(s) occur at $s=0.381607$

$$\begin{aligned} g_{\min }=0.593428, \end{aligned}$$

(25)

and the maximum value of $\big |\big \langle \frac{\mathrm{d}H(s)}{\mathrm{d}s}\big \rangle \big |$ is attained as follows

$$\begin{aligned} \max _{0<t<T}\big |\big \langle \frac{\mathrm{d}H(s)}{\mathrm{d}s}\big \rangle \big |_{s=0.392477}=1.82461. \end{aligned}$$

(26)

Now we can determine lower bound of runtime for AQC form Eq. (11)

$$\begin{aligned} T\ge \frac{1.82461}{(0.593428)^2}\frac{1}{\varepsilon }, \end{aligned}$$

(27)

which gives an estimate of the time to evolve $|\psi _0\rangle$ via adiabatic Hamiltonian (8) to attain an accuracy of order $\varepsilon$ of the final result. As an example, for accuracy of $\%90$, the lower bound of runtime should be on the order of

$$\begin{aligned} T_{\mathrm{low}}\approx \frac{1.82461}{(0.593428)^2}\frac{1}{\sqrt{1 - 0.9}}\approx 16.3845 \end{aligned}$$

(28)

in units of $\bar{T}$. Although this runtime is obtained for the input pattern $(1,1,1,1)^t$, for each pattern in its own subspace is valid.

The $\Gamma$ coefficient in the classic neural network is called learning rate and interpreted as the association between the stimulus (input) and response (output). By increasing the association between the stimulus and response, the network learns faster than before. The result of minimum evolution time for different Hamiltonian shows that similar to classic network, for the same percent of accuracy of the final state (%90), by decreasing the $\Gamma$ (decreasing the association) in Eq. (8) $T_{\mathrm{low}}$ will increase gradually (see Table 7).

Table 7 Influence of decreasing the coefficient $\Gamma$ on $T_{\mathrm{low}}$ when input patterns are partially known

The runtime of evolution to recall pattern in Sects. 4.2 and 4.3 is calculated numerically and their result presented in Table 8 for $\%90$ percent of accuracy.

Table 8 The order of minimum evolution time ($T_{\mathrm{low}}$) for accuracy of $\%90$ to recall pattern in three different cases in Sects. 4.1, 4.2 and 4.3

1.2 Runtime of AQC for partial patterns

In this case, due to the presence of unknown bits in the input pattern, the runtime of AQC is different from previous case. Here, we must repeat all calculation and finally obtain the quantities $g_{\min }$ and $D_{\max }$. The numerical results show that the Hamiltonians in Sects. 4.1 and 4.2 for all partial patterns have a specific minimum runtime (see Table 9). But as already outlined in Sect. 4.3, the QNN converges to a superposition state for partial patterns of the fourth model in Fig. 1b. The minimum energy for these patterns is zero, and thus, the quantum system cannot evolve adiabatically (see Fig. 5). Although for other models in Fig. 1b, $g_{min}$ is nonzero and the quantum system adiabatically evolve which minimum runtime ($T_{\mathrm{low}}$) for all partial patterns is 21.769 in units of $\bar{T}$ for accuracy of $\%90$ and $\Gamma =1/2$.

Table 9 The order of minimum evolution time ($T_{\mathrm{low}}$) for accuracy of $\%90$ to reterive partial pattern in Sects. 4.1, 4.2

Fig. 5

The energy gap between two lowest eigenvalues is not suitable for adiabatic evolution. Therefore, system cannot converge to retrieved pattern which is obtained in theoretical result as a superposition state