Skip to main content
SpringerLink
Log in

Triplet q-cat states of the Biedenharn–Macfarlane q-oscillator with q > 1

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

The normalized triplet q-cat states associated with three orthogonal subspaces of the Fock space representation of the Biedenharn–Macfarlane q-oscillator are constructed as eigenstates of the cubic power of the q-boson annihilation operator. Their corresponding resolution of the identity conditions by three appropriate positive definite measures in the q-integral on the whole complex plane is realized. We show that the antibunching effect and sub-Poissonian statistics as two nonclassical behaviors of the light field are demonstrated by three and two the measurable triplet q-cat states, respectively. The bipartite entanglements via the parity symmetry are another nonclassical behavior of the triplet q-cat states that are examined in this work. One remarkable property is that, contrary to the simple harmonic oscillator, the amount of entanglement in the bipartite entangled triplet q-cat states is an oscillatory function of coherency parameters and oscillation pattern depends on the deformation parameter q. In general, the entanglement becomes weaker as the parameter q increases. Clearly, the triplet q-cat states and their measures as well as the three nonclassical behaviors mentioned above are converted to their corresponding counterparts in the simple harmonic oscillator in the limit \(q\rightarrow 1\).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

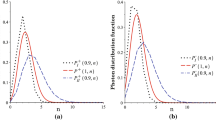
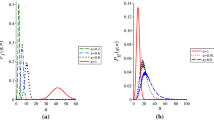
  1. Preparing the figures of this article, we have used the approximations \(C_k(|z|^2)\simeq \sum ^{100}_{n=0}\frac{q^{-\frac{3}{2}n(3n+2k+1)}|z|^{6n+2k}}{\prod _{l=1}^{3n+k} \frac{q^l-q^{-l}}{q-q^{-1}}}\) for \(k=0, 1, 2\).

References

  1. Dodonov, V.V., Malkin, I.A., Manko, V.I.: Even and odd coherent states and excitations of a singular oscillator. Physica 72, 597 (1974)

    ADS  MathSciNet  Google Scholar 

  2. Malkin, I.A., Manko, V.I.: Dynamical Symmetries and Coherent States of Quantum Systems. Nauka, Moscow (1979)

    Google Scholar 

  3. Yurke, B., Stoler, D.: Generating quantum mechanical superpositions of macroscopically distinguishable states via amplitude dispersion. Phys. Rev. Lett. 57, 13 (1986)

    ADS  Google Scholar 

  4. Xia, Y., Guo, G.: Nonclassical properties of even and odd coherent states. Phys. Lett. A 136, 281 (1989)

    ADS  Google Scholar 

  5. Buzek, V., Vidiella-Barranco, A., Knight, P.L.: Superpositions of coherent states: squeezing and dissipation. Phys. Rev. A 45, 6570 (1992)

    ADS  Google Scholar 

  6. Brune, M., Hagley, E., Dreyer, J., Maitre, X., Maali, A., Wunderlich, C., Raimond, J.M., Haroche, S.: Observing the progressive decoherence of the “meter” in a quantum measurement. Phys. Rev. Lett. 77, 4887 (1996)

    ADS  Google Scholar 

  7. Agarwal, G.S., Puri, R.R., Singh, R.P.: Atomic Schrödinger cat states. Phys. Rev. A 56, 2249 (1997)

    ADS  Google Scholar 

  8. Gerry, C.C., Knight, P.L.: Quantum superpositions and Schrödinger cat states in quantum optics. Am. J. Phys. 65, 964 (1997)

    ADS  Google Scholar 

  9. Leghtas, Z., Touzard, S., Pop, I.M., Kou, A., Vlastakis, B., Petrenko, A., Sliwa, K.M., Narla, A., Shankar, S., Hatridge, M.J., Reagor, M., Frunzio, L., Schoelkopf, R.J., Mirrahimi, M., Devoret, M.H.: Confining the state of light to a quantum manifold by engineered two-photon loss. Science 347, 853 (2015)

    ADS  Google Scholar 

  10. Joo, J., Elliott, M., Oi, D.K.L., Ginossar, E., Spiller, T.P.: Deterministic amplification of Schrödinger cat states in circuit quantum electrodynamics. New J. Phys. 18, 023028 (2016)

    ADS  Google Scholar 

  11. Gerry, C.C., Grobe, R.: Nonclassical properties of correlated two-mode Schrödinger cat states. Phys. Rev. A 51, 1698 (1995)

    ADS  Google Scholar 

  12. Gerry, C.C., Grobe, R.: Two-mode \(SU(2)\) and \(SU(2)\) schrödinger cat states. J. Mod. Opt. 44, 41 (1997)

    ADS  MATH  Google Scholar 

  13. Haroche, S., Raimond, J.-M.: Exploring the Quantum: Atoms. Oxford University Press, Oxford (2006)

    MATH  Google Scholar 

  14. Arik, M., Coon, D.D.: Hilbert spaces of analytic functions and generalized coherent states. J. Math. Phys. 17, 524 (1976)

    ADS  MathSciNet  MATH  Google Scholar 

  15. Biedenharn, L.C.: The quantum group \(SU_q(2)\) and a \(q\)-analogue of the boson operators. J. Phys. A Math. Gen. 22, L873 (1989)

    ADS  MATH  Google Scholar 

  16. Macfarlane, A.J.: On \(q\)-analogues of the quantum Harmonic oscillator and the quantum group \(SU(2)\). J. Phys. A Math. Gen. 22, 4581 (1989)

    ADS  MATH  Google Scholar 

  17. Dey, S.: \(q\)-deformed noncommutative cat states and their nonclassical properties. Phys. Rev. D 91, 044024 (2015)

    ADS  Google Scholar 

  18. Fakhri, H., Hashemi, A.: Nonclassical properties of the \(q\)-coherent and \(q\)-cat states of the Biedenharn–Macfarlane \(q\) oscillator with \(q>1\). Phys. Rev. A 93, 013802 (2016)

    ADS  Google Scholar 

  19. Fakhri, H., Nouraddini, M.: Right \(SU_q(2)\)- and left \(SU_{q^{-1}}(2)\)-invariances of the \(q\)-Hilbert–Schmidt scalar products for an adjoint representation of the quantum algebra \(\breve{U}_q(su_2)\). J. Geom. Phys. 110, 90 (2016)

    ADS  MathSciNet  MATH  Google Scholar 

  20. Fakhri, H., Sayyah-Fard, M.: Arik-Coon \(q\)-oscillator cat states on the noncommutative complex plane \({\mathbb{C}}_{q^{-1}}\) and their nonclassical properties. Int. J. Geom. Meth. Mod. Phys. 14, 1750060 (2017)

    MATH  Google Scholar 

  21. Fakhri, H., Sayyah-Fard, M.: Nonclassical properties of the Arik–Coon \(q^{-1}\)-oscillator coherent states on the noncommutative complex plane \({\mathbb{C}}_q\). Int. J. Geom. Meth. Mod. Phys. 14, 1750165 (2017)

    MATH  Google Scholar 

  22. Fakhri, H., Sayyah-Fard, M.: \(q\)-coherent states associated with the noncommutative complex plane \({\mathbb{C}}_q^2\) for the Biedenharn–Macfarlane \(q\)-oscillator. Ann. Phys. 387, 14 (2017)

    ADS  MATH  Google Scholar 

  23. Kuang, L.-M., Wang, F.-B.: The \(su_q(1,1)\) \(q\)-coherent states and their nonclassical properties. Phys. Lett. A 173, 221 (1993)

    ADS  MathSciNet  Google Scholar 

  24. Roy, B., Roychoudhury, R.: Even and odd \(q\)-coherent states in a finite-dimensional basis and their squeezing properties. Int. J. Theor. Phys. 36, 1525 (1997)

    MathSciNet  MATH  Google Scholar 

  25. Wang, J.-S., Wang, B.-Y., Sun, C.-Y.: Even and odd \(qs\)-coherent states and their photon-statistical properties. Phys. Lett. A 246, 464 (1998)

    ADS  MathSciNet  MATH  Google Scholar 

  26. Zhao, Y., Zeng, Y., Liu, H., Song, Q., Wang, G., Xue, K.: \(q\)-deformed Barut–Girardello \(su(1,1)\) coherent states and Schrödinger cat states. Theory. Math. Phys. 193, 1844 (2017)

    MATH  Google Scholar 

  27. Dodonov, V.V.: ‘Nonclassical’ states in quantum optics: a ‘squeezed’ review of the first 75 years. J. Opt. B: Quantum Semiclass. Opt. 4, R1 (2002)

    ADS  MathSciNet  Google Scholar 

  28. Rosas-Ortiz, O., Cruzy Cruz, S., Enriquez, M.: \(SU(1,1)\) and \(SU(2)\) approaches to the radial oscillator: generalized coherent states and squeezing of variances. Ann. Phys. 373, 346 (2016)

    ADS  MathSciNet  MATH  Google Scholar 

  29. Paul, H.: Photon antibunching. Rev. Mod. Phys. 54, 1061 (1982)

    ADS  Google Scholar 

  30. Mandel, L.: Sub-Poissonian photon statistics in resonance fluorescence. Opt. Lett. 4, 205 (1979)

    ADS  Google Scholar 

  31. Divincenzo, D.P.: Quantum computation. Science 270, 255 (1995)

    ADS  MathSciNet  MATH  Google Scholar 

  32. Gerry, C., Knight, P.: Introductory Quantum Optics. Cambridge University Press, New York, Melbourne (2005)

    Google Scholar 

  33. Bennett, C.H., Brassard, G., Crepeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 70, 1895 (1993)

    ADS  MathSciNet  MATH  Google Scholar 

  34. Bennett, C.H., Wiesner, S.J.: Communication via one- and two-particle operators on Einstein–Podolsky–Rosen states. Phys. Rev. Lett. 69, 2881 (1992)

    ADS  MathSciNet  MATH  Google Scholar 

  35. Murao, M., Jonathan, D., Plenio, M.B., Vedral, V.: Quantum telecloning and multiparticle entanglement. Phys. Rev. A 59, 156 (1999)

    ADS  Google Scholar 

  36. Petz, D.: Quantum Information Theory and Quantum Statistics. Springer, Berlin (2008)

    MATH  Google Scholar 

  37. Wootters, W.K.: Entanglement of formation and concurrence. Quant. Inf. Comput. 1, 27 (2001)

    MathSciNet  MATH  Google Scholar 

  38. Akhtarshenas, S.J.: Concurrence vectors in arbitrary multipartite quantum systems. J. Phys. A: Math. Gen. 38, 6777 (2005)

    ADS  MathSciNet  MATH  Google Scholar 

  39. Bennett, C.H., Bernstein, H.J., Popescu, S., Schumacher, B.: Concentrating partial entanglement by local operations. Phys. Rev. A 53, 2046 (1996)

    ADS  Google Scholar 

  40. Zyczkowski, K., Horodecki, P., Sanpera, A., Lewenstein, M.: Volume of the set of separable states. Phys. Lett. A 58, 883 (1998)

    MathSciNet  Google Scholar 

  41. Coffman, V., Kundu, J., Wootters, W.K.: Distributed entanglement. Phys. Lett. A 61, 052306 (2000)

    Google Scholar 

  42. Wong, A., Christensen, N.: Potential multiparticle entanglement measure. Phys. Lett. A 63, 044301 (2001)

    Google Scholar 

  43. Plenio, M.B., Vedral, V.: Entanglement in quantum information theory. Contemp. Phys. 39, 431 (1998)

    ADS  Google Scholar 

  44. Nielsen, M.A.: Conditions for a class of entanglement transformations. Phys. Rev. Lett. 83, 436 (1999)

    ADS  Google Scholar 

  45. Berrada, K., El Baz, M., Saif, F., Hassouni, Y., Mnia, S.: Entanglement generation from deformed spin coherent states using a beam splitter. J. Phys. A Math. Theor. 42, 285306 (2009)

    MathSciNet  MATH  Google Scholar 

  46. Fu, H., Wang, X., Solomon, A.I.: Maximal entanglement of nonorthogonal states: classification. Phys. Lett. A 291, 73 (2001)

    ADS  MathSciNet  MATH  Google Scholar 

  47. Wang, X.: Bipartite entangled non-orthogonal states. J. Phys. A Math. Gen. 35, 165 (2002)

    ADS  MathSciNet  MATH  Google Scholar 

  48. Behzadi, N.: Genuine three-partite entanglement in coherent states via permutation and parity symmetries. Quantum Inf. Process. 12, 21 (2013)

    ADS  MathSciNet  MATH  Google Scholar 

  49. Sanders, B.C.: Entangled coherent states. Phys. Rev. A 45, 6811 (1992)

    ADS  Google Scholar 

  50. Wang, X., Sanders, B.C., Pan, S.H.: Entangled coherent states for systems with \(SU(2)\) and \(SU(1,1)\) symmetries. J. Phys. A Math. Gen. 33, 7451 (2000)

    ADS  MathSciNet  MATH  Google Scholar 

  51. Sanders, B.C.: Review of entangled coherent states. J. Phys. A Math. Theor. 45, 244002 (2012)

    ADS  MathSciNet  MATH  Google Scholar 

  52. Fuchs, C.A.: Nonorthogonal quantum states maximize classical information capacity. Phys. Rev. Lett. 79, 1162 (1997)

    ADS  Google Scholar 

  53. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009)

    ADS  MathSciNet  MATH  Google Scholar 

  54. De Martini, F., Fortunato, M., Tombesi, P., Vitali, D.: Generating entangled superpositions of macroscopically distinguishable states within a parametric oscillator. Phys. Rev. A 60, 1636 (1999)

    ADS  Google Scholar 

  55. Landau, M.A., Stroud Jr., C.R.: Calculation of the convex roof for an open entangled harmonic oscillator system. Phys. Rev. A 81, 052304 (2010)

    ADS  Google Scholar 

  56. Sheng, Y.-B., Zhou, L.: Entanglement analysis for macroscopic Schrödinger’s Cat state. EPL 109, 40009 (2015)

    ADS  Google Scholar 

  57. Berrada, K., El Baz, M., Eleuch, H., Hassouni, Y.: Bipartite entanglement of nonlinear quantum systems in the context of the \(q\)-Heisenberg Weyl algebra. Quantum Inf. Process. 11, 351 (2012)

    MathSciNet  MATH  Google Scholar 

  58. Corcoles, A.D., et al.: Protecting superconducting qubits from radiation. Appl. Phys. Lett. 99, 181906 (2011)

    ADS  Google Scholar 

  59. Dong, L., et al.: Single-photon controlled multi-photon polarization unitary gate based on weak cross-Kerr nonlinearities. Quantum Inf. Process. 17, 114 (2018)

    ADS  MathSciNet  MATH  Google Scholar 

  60. Kirchmair, G., et al.: Observation of quantum state collapse and revival due to the single-photon Kerr effect. Nature 495, 205 (2013)

    ADS  Google Scholar 

  61. Klimyk, A., Schmüdgen, K.: Quantum Groups and Their Representations. Springer, Berlin (1997)

    MATH  Google Scholar 

  62. Apostol, T.M.: Introduction to Analytic Number Theory. Springer, New York (1976)

    MATH  Google Scholar 

  63. Horne, M.A., Shimony, A., Zeilinger, A.: Two-particle interferometry. Phys. Rev. Lett. 62, 2209 (1989)

    ADS  Google Scholar 

Download references

Acknowledgements

This research has been supported by the University of Tabriz under Grant S/3899.

Author information

Authors and Affiliations

  1. Department of Theoretical Physics and Astrophysics, Faculty of Physics, University of Tabriz, P. O. Box 51666-16471, Tabriz, Iran

    H. Fakhri & M. Sayyah-Fard

Authors
  1. H. Fakhri
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Sayyah-Fard
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Sayyah-Fard.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fakhri, H., Sayyah-Fard, M. Triplet q-cat states of the Biedenharn–Macfarlane q-oscillator with q > 1. Quantum Inf Process 19, 19 (2020). https://doi.org/10.1007/s11128-019-2507-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-019-2507-z

Keywords

Search

Navigation