Skip to main content
SpringerLink
Log in

Cellular automaton simulation of the quantum Hotelling game with reservation cost

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

This work studies the quantum Hotelling game via spatial numerical simulation. It is concluded that entanglement enables the emergence of the Pareto optimal solution in Nash equilibrium in simulations of the game with variable prices and fixed location of the players. In the rather complicated scenario of variable prices and locations, the implemented simulation technique shows that the players share the market, both locating close to (L/4, 3L/4). The Hotelling game is studied with both linear and quadratic transportation cost, with no relevant discrepancies found in both scenarios.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30

Similar content being viewed by others

Notes

  1. \( p_2^c-p_1^c =p_2w_1+p_1w_2-(p_1w_1+p_2w_2)= p_2(w_1-w_2) -p_1(w_1-w_2)=(p_2-p_1)(w_1-w_2).\)

  2. \(u_1^c=p_1^c(Q_1(\gamma )={{\overline{s}}}(\gamma ))\), \(u_2^c=p_2^c(Q_2(\gamma )=(L-{{\overline{s}}}(\gamma )))\), \(\partial {{u_1(\gamma )}}{{p_1}}=0\,\cap \,\partial {{u_2(\gamma )}}{{p_2}}=0 \rightarrow p_1^\star (\gamma ),p_2^\star (\gamma ).\)

  3. \(e(s)=\alpha \rightarrow p_1^c+(s-a)t=\alpha ,\, p_2^c+(L-b-s)t=\alpha , \rightarrow p_1^c+p_2^c=2\alpha -(L-b-a)t \rightarrow (p_1+p_2)(w_1+w_2)=h\). \(\frac{p_1}{p_2}=\frac{L+k(\gamma )}{L-k(\gamma )} \rightarrow (p_1+ \frac{L-k(\gamma )}{L+k(\gamma )}p_1)(w_1+w_2)=h,\,\, p_1(\frac{2L}{L+k(\gamma )})(w_1+w_2)=h\,.\)

  4. \(\gamma \ge \gamma ^\bullet :\, p_2^\star (\gamma )-p_1^\star (\gamma )= \frac{he^{-\gamma }}{2L}[-2k(\gamma )]t\). .

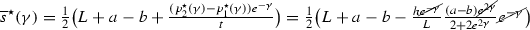  5. \(\frac{1}{2}\big (L +\frac{a-b}{2+e^{2\gamma }}\big )=\frac{1}{2}\big (L+a-b - \frac{h(a-b)}{L(2+e^{2\gamma })}\big )\Rightarrow \) \( \frac{a-b}{2+e^{2\gamma }} = a-b - \frac{h(a-b)}{L(2+e^{2\gamma })} \Rightarrow \) \( \frac{1}{2+e^{2\gamma }} = 1 - \frac{h}{L(2+e^{2\gamma }(} \Rightarrow \) \( 1 = 2+e^{2\gamma } - \frac{h}{L} \Rightarrow \) \( e^{2\gamma }= \frac{h}{L}-1\,.\)

  6. Both \({{\overline{s}}}^\star (\gamma )\) formulas equalize at \(\gamma =\gamma ^\bullet \) :  \(\frac{1}{2}\big (L +\frac{a-b}{2+e^{2\gamma }}\big )=\frac{1}{2}\big (L+a-b - \frac{h(a-b)}{L(2+e^{2\gamma })(x_2-x_1)}\big )\Rightarrow \) \( \frac{a-b}{2+e^{2\gamma }} = a-b - \frac{h(a-b)}{L(2+e^{2\gamma })(x_2-x_1)} \Rightarrow \) \( \frac{1}{2+e^{2\gamma }} = 1 - \frac{h}{L(2+e^{2\gamma })(x_2-x_1)} \Rightarrow \) \( 1 = 2+e^{2\gamma } - \frac{h}{x_2-x_1} \Rightarrow \) \( e^{2\gamma }= \frac{h}{L(x_2-x_1)}-1\,.\)

  7. \( p_2^c-p_1^c =p_2w_1(\gamma )+p_1w_2(\gamma )-(p_1w_1(\gamma )+p_2w_2(\gamma ))= p_2(w_1(\gamma )-w_2(\gamma )) -p_1(w_1(\gamma )-w_2(\gamma ))=(p_2-p_1)(w_1(\gamma )-w_2(\gamma )), w_1(\gamma )-w_2(\gamma )= \cos ^2\gamma -\sin ^2\gamma =\cos 2\gamma \).

  8. Both \({{\overline{s}}}^\star (\gamma )\) formulas equalize at \(\gamma =\gamma ^\bullet \) :  \(\frac{1}{2}\big (L+a-b-2\frac{\cos ^2\gamma }{\cos 2\gamma }k(\gamma )\big )=\frac{1}{2}\big (L+a-b-\frac{h}{L}k(\gamma )\big )\Rightarrow \) \( 2\frac{\cos ^2\gamma }{\cos 2\gamma } = \frac{h}{L} \Rightarrow \) \( \frac{\cos ^2\gamma -\sin ^2\gamma }{\cos ^2\gamma } = \frac{2L}{h} \Rightarrow \) \( 1-\tan ^2 \gamma = \frac{2L}{h}\,. \)

References

  1. Alonso-Sanz, R., Adamatzky, A.: Cellular automaton simulation of the quantum war of attrition game. Quantum Inf. Process. 19(10), 1–20 (2020)

    Article  MathSciNet  Google Scholar 

  2. Alonso-Sanz, R., Adamatzky, A.: Spatial simulation in the quantum Bertrand duopoly game. Physica A 557, 124867 (2020)

    Article  MathSciNet  Google Scholar 

  3. Alonso-Sanz, R., Martin-Gutierrez, S.: The free-rider in the quantum Stackelberg duopoly game. Physica A 554, 124271 (2020)

    Article  MathSciNet  Google Scholar 

  4. Alonso-Sanz, R.: Simulation of the quantum Cournot duopoly game. Physica A 534, 122116 (2019)

    Article  MathSciNet  Google Scholar 

  5. Alonso-Sanz, R.: Quantum Game Simulation. Springer, Berlin (2019)

    Book  Google Scholar 

  6. Alonso-Sanz,R.(2017). Spatial correlated games. Royal Society Open Science, 4,6,171361

  7. d’Aspremont, C., Gabszewicz, J.J., Thisse, J.F.: On Hotelling’s “Stability in competition’’. Econometrica 47(5), 1145–1150 (1979)

    Article  MathSciNet  Google Scholar 

  8. Chen, Y., Qin, G., Wang, A.M.: Quantization of the Location Stage of Hotelling Model. arXiv preprint arXiv:1410.2779 (2014)

  9. Du, J., Ju, C., Li, H.: Quantum entanglement helps in improving economic efficiency. J. Phys. A Math. General 38(7), 1559 (2005)

    Article  MathSciNet  ADS  Google Scholar 

  10. Economides,N.(1993). Hotelling’s ’Main Street’ with more than two competitors. Journal of Regional Science,33(3), 303-319

  11. Eisert, J., Wilkens, M., Lewenstein, M.: Quantum games and quantum strategies. Phys. Rev. Lett. 83(15), 3077–3080 (1999)

    Article  MathSciNet  ADS  Google Scholar 

  12. Frackiewicz, P.: Remarks on quantum duopoly schemes. Quantum Inf. Process. 15(1), 121–136 (2016)

    Article  MathSciNet  ADS  Google Scholar 

  13. Hinloopen, J., Van Marrewijk, C.: On the limits and possibilities of the principle of minimum differentiation. Int. J. Ind. Organ. 17(5), 735–750 (1999)

    Article  Google Scholar 

  14. Hotelling, H.: Stability in competition. Econ. J. 39(153), 41–57 (1929)

    Article  Google Scholar 

  15. Iqbal, A., Chappell, J.M., Abbott, D.: On the equivalence between non-factorizable mixed-strategy classical games and quantum games. R. Soc. Open Sci. 3, 150477 (2016)

    Article  MathSciNet  ADS  Google Scholar 

  16. Li, H., Du, J., Massar, S.: Continuous-variable quantum games. Phys. Lett. A 306, 73–78 (2002)

    Article  MathSciNet  ADS  Google Scholar 

  17. Lerner, A.P., Singer, H.W.: Some notes on duopoly and spatial competition. J. Political Econ. 45(2), 145–186 (1937)

    Article  Google Scholar 

  18. Lo, C.F., Kiang, D.: Quantum Stackelberg duopoly. Phys. Lett. A 318, 333–336 (2003)

    Article  MathSciNet  ADS  Google Scholar 

  19. Lo, C.F., Kiang, D.: Quantum Bertrand duopoly with differentiated products. Phys. Lett. A 321(2), 94–98 (2004)

    Article  MathSciNet  ADS  Google Scholar 

  20. Rahaman, R., Majumdar, P., Basu, B.: Quantum Cournot equilibrium for the Hotelling-Smithies model of product choice. J. Phys. A Math. Theor. 45(45), 455301 (2012)

    Article  MathSciNet  Google Scholar 

  21. Wolfram, S.: A New Kind of Science. Wolfram Media, Champaign (2002)

    MATH  Google Scholar 

Download references

Acknowledgements

This work has been funded by the Spanish Grant PGC2018-093854-B-I00. The computations of this work were performed in FISWULF, an HPC machine of the International Campus of Excellence of Moncloa, funded by the UCM and Feder Funds.

Author information

Authors and Affiliations

  1. Complex Systems Group, Universidad Politénica de Madrid, C. Universitaria, Madrid, 28040, Spain

    Luis Garcia, Juan Grau, Juan C. Losada & Ramon Alonso-Sanz

Authors
  1. Luis Garcia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Juan Grau
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Juan C. Losada
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ramon Alonso-Sanz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ramon Alonso-Sanz.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Garcia, L., Grau, J., Losada, J.C. et al. Cellular automaton simulation of the quantum Hotelling game with reservation cost. Quantum Inf Process 20, 227 (2021). https://doi.org/10.1007/s11128-021-03132-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-021-03132-x

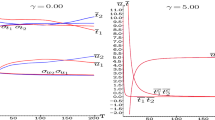
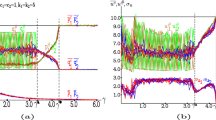
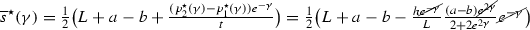Keywords

Search

Navigation