The security of quantum noise stream cipher against collective attacks

Abstract

Quantum noise stream cipher (QNSC), where signal states are masked by intrinsic quantum noise to directly encrypt data, provides a physical layer security. This paper firstly discusses the security of the QNSC system under the assumption that eavesdropper is restricted to collective attacks. The maximum security capacity for the encrypted data, the running key, and the entire system is derived, respectively. Our simulation results allow a positive information capacity when data transmission distance is no more than 300 km for the number of bases $M_\mathrm{{b}} = 31$ and any mean photon number $\alpha ^2$ by assuming state-of-the-art technology. We find that the security of whole system depends on the security of running key for shorter distances. However, the security of whole system is related to the security of data for longer distances. Furthermore, it is important to improve security of data in QNSC system for longer distances. Besides, this new method proposes a concrete solution for physical encryption systems and paves the way for a wider implementation of the QNSC system.

1 Introduction

With the rapid development of optical communication, more and more messages, such as personal privacy information, bank account, and confidential information, are transmitted through optical link. Protecting these messages from eavesdropping is a major challenge in optical communication. To cope with this problem, physical layer security based on physical effects has been attracted more and more attention. The physical effects, such as noise [1], chaos [2, 3], mode dependent loss (MDL) [4], and nonlinear effects, are used to encrypt data applying encryption based on physical layer security. In this way, eavesdroppers are faced with the arduous task of recording and storing accurate ciphertext under the impact of physical effects [5,6,7]. Thus, physical layer encryption has better security in comparison with traditional encryption method. Quantum noise stream cipher provides physical layer security, while being compatible with current networks, is getting more and more attention.

Quantum noise stream cipher (QNSC), also known as Y-00 protocol, was first proposed by Horace P. Yuen and achieves the data encryption and secure communication by expanding the influence of quantum noise on eavesdropper’s signal states [8]. Thanks to the intrinsic quantum noise from the coherent state, Eve cannot completely distinguish the adjacent signal states when encrypted signal is masked by quantum noise [9]. In addition, QNSC can achieve the physical layer security imposing less restriction compared with quantum key distribution protocols [10]. Many experiments have been reported for different modulation formats, such as phase shift-key (PSK) [11, 12], quadrature amplitude modulation (QAM) [13,14,15], and intensity shift-key (ISK) [16, 17]. However, it is under debate whether QNSC can have nonzero secure rate under the quantum attacks hypothesis, such as collective attacks [18, 19]. Furthermore, perfect security analysis of QNSC is complex since each symbol bit is encoded into the coherent state living in an infinite-dimensional Hilbert space [20,21,22]. By building the wire-tap channel model for both channels of the key and data, the security analysis of QNSC has been studied [23,24,25,26]. However, in its traditional and classical method of security analysis, the security capacity of data and key is overestimated by the state-of-the-art model. Eve has a better ability to obtain more useful information, even though the signals are masked by quantum noise, for example using collective attacks [27]. It is a major challenge to construct a security analysis of QNSC system against collective attacks.

In this paper, we investigate the security ability of QNSC based on PSK modulation under the collective attacks hypothesis. The same strategy could be applied to different modulation formats as well. The maximum security rate for the data, the running key, and the whole system is derived, respectively. Simulation results show that the QNSC can achieve nonzero secure rate, even if Eve has access to the quantum channel performing collective attacks on the system. QNSC system allows a positive information capacity when data transmission is no more than 300 km link for the number of bases $M_\mathrm{{b}} = 31$ and any mean photon number $\alpha ^2$. The security of the data is more vulnerable in comparison with the running key for longer distances in the QNSC system. Thus, it is important to improve the security of the data for longer distance. We believe that this security analysis can pave the way toward a perfect security analysis of QNSC system, under quantum mechanics.

2 The principle of QNSC based on PSK modulation in detail

First, the transmitter, Alice, has to share a K-bit seed key with Bob (the receiver) to generate the running key U by a linear feedback shift register (LFSR) or AES in stream cipher mode. Then, the running key U is divided into n sub-blocks u with M bit as bases. (The number of bases $M_\mathrm{{b}}=2^M-1$.) According to the mapping rule, running key $U=\left\{ u^1,u^2,...,u^n\right\}$ is used to encrypt the n-bit data $X= \left\{ x^1,x^2,...,x^n\right\}$ to generate the encrypted data stream. The BPSK/QNSC signal is given as follows [11]:

$$\begin{aligned} \left| \phi _m\right\rangle = \left| \alpha e^{i\theta _m}\right\rangle =\left| \alpha e^{i\frac{\pi }{M_\mathrm{{b}}}m}\right\rangle \end{aligned}$$

(1)

where i is an imaginary unit and $\alpha ^2$ is the intensity (mean photon number) of the coherent state. The $\theta _m$ in Eq. (1) is the phase of the coherent state and is given as follows:

$$\begin{aligned}&\theta _m = (\hbox {Pol}(u) \oplus x) \cdot \pi +\frac{\pi }{M_\mathrm{{b}}} \cdot \hbox {Dec}(u) \end{aligned}$$

(2)

$$\begin{aligned}&\hbox {Pol}(u) = {\left\{ \begin{array}{ll} 1 &{} u \hbox { is odd} \\ 0 &{} u \hbox { is even} \end{array}\right. } \end{aligned}$$

(3)

where $\hbox {Dec}$(u) represents decimal arithmetic on u and $\oplus$ is binary XOR operation. Figure 1 shows the constellation of BPSK/QNSC system in phase space. By Eqs. (1), (2), and (3), the data bits 0 and 1 are mapped into phase space with different angles, as shown in Fig. 1a. Then, signal states are masked by quantum noise (shot noise) from laser when encrypted signals are modulated by phase modulator and laser, as shown in Fig. 1b. In the absence of running key U, eavesdropper, Eve, has to distinguish and record the signal states under the effects of quantum noise in transmission. Due to the small difference between adjacent signals masked by quantum noise, Eve cannot obtain accurate information. However, as a legal receiver, Bob, who shares the running key U with Alice at the beginning, only needs to detect binary signal states, as shown in Fig. 1c. So, compared with Eve, Bob can accurately recover signal states with a little effect of quantum noise. However, Eve has to distinguish the super-high-order signal states under the impact of quantum noise in Fig. 1b. It is difficult for Eve to eliminate the effects of quantum noise on signal states and then accurately distinguish adjacent signal states. So, based on quantum noise from the coherent state, QNSC system can directly encrypt data to provide physical layer security.

Fig. 1

The constellation of QNSC based on PSK in phase space: a the encoding of signal states in the transmitter; b the signal states received by the eavesdropper; c the decoding of signal states in the legal receiver

3 Security analysis of QNSC system under collective attacks

Fig. 2

The diagrams of QNSC system on data flow processing. Here, the transmission coefficient of channel between Alice and Bob is $\eta$. PM, phase modulator; VOA, variable optical attenuator; LO, local oscillator; DSP, digital signal processor

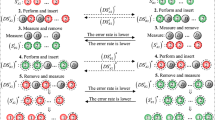
The data streams from Alice to Bob are schematically shown in Fig. 2. We find that the transmitted signal states $\left| \phi _m\right\rangle$ contain not only information of data bits x but also information of the running key u in QNSC system. Firstly, the security of data bits x and running key u is discussed, respectively. Subsequently, the systematic security of QNSC system is derived. The systematic security of QNSC depends on the minimum between secret information rate of data bit x and secret information rate of running key u. In the QNSC system, the systematic security rate per bit, R, is given by [24]

$$\begin{aligned} R = \min \left\{ R_\mathrm{{data}}, R_\mathrm{{key}}\right\} \end{aligned}$$

(4)

where the $R_\mathrm{{data}}$ and $R_\mathrm{{key}}$ denote the secure rate of data bits x and running key u in QNSC, respectively.

We assume that Eve has a quantum computer and quantum memory to handle signal states from quantum channel. For collective attacks, Eve can utilize each probe state separately to interact with signal states. Then, Eve stores the probe states in a quantum memory and then performs the collective quantum measurement on probe states to get more information. And, there is no excess noise in the quantum channel and Eve’s measurement is limited only by quantum noise [28]. The transmission coefficient of the channel connecting Alice and Bob is $\eta$ ($\eta =10^{-\frac{\hbox {loss}}{10}}$). Here, $\hbox {loss}=0.2 \times d$. The loss of quantum channel is $0.2\,\hbox {dB/km}$. Eve inserts the beam splitter into the quantum channel to intercept the $(1-\eta )$ signals and sends the partial $\eta$ signal states to Bob by a lossless quantum channel. The quantum channel of data x is given as follows in Fig. 2.

$$\begin{aligned} x_{0/1}{\mathop {\longrightarrow }\limits ^{u}} \left| \phi _m\right\rangle {\mathop {\longrightarrow }\limits ^{\hbox {channel}}} \left| \beta _m\right\rangle {\mathop {\longrightarrow }\limits ^{u}} \tilde{x}_{0/1}. \end{aligned}$$

(5)

The quantum channel of data bit x is binary discrete memoryless channel (DMC) because Alice and Bob have same running key u for each communication in QNSC. However, the quantum channel between Alice and Eve is not memoryless channel in a strict sense due to the application of LFSR and ASE for QNSC in practice. The correlation of running key u is every weak due to the influence of quantum noise. And, we can replace LFSR and ASE in QNSC with longer random running key if QNSC system does not provide high rate but achieves high security. So, we assume that the information Eve gets from channel is given as $I(A,E)+\delta$, where $\delta$ ($\delta \ge 0$ and $\delta \rightarrow 0$ due to quantum noise) is the information Eve obtains due to weak correlation of running key u. Here, $\delta$ is a tiny constant and depends on the complexity of key expansion. (It is beyond our scope in this paper.) Furthermore, based on classical wire-tap channel model, this assumption has been discussed by Jiao and co-authors [24]. So, we mainly discuss the security capacity of data $R_\mathrm{{data}}$ and running key $R_\mathrm{{key}}$ with memoryless channel, and these are the maximum in QNSC system under this assumption. Besides, it also provides the reference to the design of key expansion in QNSC.

For given signal $\left| \phi _m\right\rangle$ from Alice, Bob measures it by splitting the signal at a 50/50 beam splitter and measuring two conjugate quadrature $\hat{x}$ and $\hat{p}$ at the output ports by heterodyne detection. The received signal states are $\left| \beta _m\right\rangle = \left| \beta _x+i\beta _p\right\rangle$ when measurement results are $\beta _x$ and $\beta _p$. The conditional probability density to measure the state $\left| \beta \right\rangle$ when a state $\left| \phi _m\right\rangle$ has been sent is

$$\begin{aligned} p(\beta |\phi _m) = \frac{1}{\pi }e^{-|\beta -\phi _m|}. \end{aligned}$$

(6)

After the measurement of $\left| \beta \right\rangle$, the conditional probability $p(\phi _l|\beta )$ can be calculated when state $\left| \phi _l\right\rangle$ was sent initially by Eq. (6) and Bayes theorem

$$\begin{aligned} {\left\{ \begin{array}{ll} p(\phi _l|\beta ) = \frac{p(\beta |\phi _l)}{2M_\mathrm{{b}}p(\beta )} =\frac{1}{2M_\mathrm{{b}}\pi p(\beta )}e^{-|\beta -\phi _l|}\\ p(\beta ) = \frac{1}{2M_\mathrm{{b}}}\begin{matrix} \sum _l^{2M_\mathrm{{b}}}p(\beta |\phi _l) \end{matrix} \end{array}\right. } \end{aligned}$$

(7)

where the transmitted signal states are uniformly distributed.

After measuring transmitted signal states, Bob decodes the measured states to get a value. When $\phi _l=\phi _m$ in Eqs. (6) and (7), Bob can correctly decode the data. Otherwise, Bob cannot correctly decode the data. Bob shares the seed key with Alice, and the quantum channel connecting Alice and Bob for data is binary DMC. Thus, the conditional density $p(\beta |\phi _{l})$ can be simplified as follows:

$$\begin{aligned} p(\beta _{\tilde{x},u}|\phi _{x,u}) = \frac{1}{\pi }e^{-|\beta _{\tilde{x},u} -\phi _{x,u}|}, \quad \forall u = 0 \sim M_d-1. \end{aligned}$$

(8)

Finally, the amount of information transmitted from Alice to Bob on data x is given as follows:

$$\begin{aligned} I^{x}(A,B)&= H(B)- H(B|A)\nonumber \\&= \log _2(2) + \int p(\phi _{x,u})\begin{matrix} \sum _{\tilde{x}} p(\beta _{\tilde{x},u}|\phi _{x,u}) \log _2 p(\beta _{\tilde{x},u}|\phi _{x,u}) \end{matrix} \end{aligned}$$

(9)

where H(B) and H(B|A) are the Shannon entropy and conditional entropy, respectively.

The information that Eve may extract is given by the Holevo quantity under collective attacks [27]. For data x, the Holevo information between Alice and Eve is given as follows:

$$\begin{aligned} I^{x}(A,E) = S(\rho _E^{x}) - \sum _{k}p_k S(\rho _{E|k}^{x}),\quad k \in \left\{ 0,1\right\} \end{aligned}$$

(10)

where $\rho _E = \sum _{k}p_k \rho _{E|k}$ and $S(\rho ) =-\hbox {Tr}\left\{ \rho \log (\rho )\right\}$ is the von Neumann entropy. The $\rho$ is the quantum density operator and $\rho =p_m\left| \phi _m\right\rangle \left\langle \phi _m\right|$ for any pure states $\left| \phi _m\right\rangle$, where $p_m$ is the probability of pure states $\left| \phi _m\right\rangle$. According to the attack model, Eve’s states conditioned on Alice’s preparation are

$$\begin{aligned} \left| \varepsilon _m\right\rangle = \left| \sqrt{(1-\eta )}\phi _m\right\rangle =\left| \sqrt{(1-\eta )}\alpha e^{i\frac{\pi }{M_\mathrm{{b}}}m}\right\rangle . \end{aligned}$$

(11)

Therefore, when transmitted data x is 0, the density operator $\rho _{E|0}^{x}$ for Eve’s signal state is

$$\begin{aligned} \rho _{E|0}^{x} = \frac{1}{M_\mathrm{{b}}}\sum _{m=0}^{M_\mathrm{{b}}-1}\left| \varepsilon _{2m}\right\rangle \left\langle \varepsilon _{2m}\right| = \frac{1}{M_\mathrm{{b}}}\sum _{k=0}^{M_\mathrm{{b}}-1} \left| \varepsilon _{k}\right\rangle \left\langle \varepsilon _{k}\right| \end{aligned}$$

(12)

where $k=2m$ and density matrix $\rho _{E|0}^{x}$ is Eve’s state conditioned on preparation of data bit 0. To calculate the von Neumann entropy of density operator $\rho _{E|0}^{x}$, the eigenvalues of density operator $\rho _{E|0}^{x}$ have to be derived. Based on orthogonal basis $\left| \xi _n\right\rangle$, symmetric states $\left| \epsilon _k\right\rangle$ can be expressed as follows [29, 30]:

$$\begin{aligned} \left| \varepsilon _k\right\rangle =\left| \sqrt{(1-\eta )}\alpha e^{i\frac{2\pi }{M_\mathrm{{b}}}k}\right\rangle =\sum _{n=0}^{M_\mathrm{{b}}-1}a_n e^{i\frac{2\pi }{M_\mathrm{{b}}}k}\left| \xi _n\right\rangle , \quad k\in \left\{ 0,1,...,M_\mathrm{{b}}-1\right\} . \end{aligned}$$

(13)

The density matrix $\rho _{E|0}^{x}$ can be diagonalized by the orthogonal basis $\left| \xi _n\right\rangle$ as follows:

$$\begin{aligned} \rho _{E|0}^{x} = \frac{1}{M_\mathrm{{b}}}\sum _{k=0}^{M_\mathrm{{b}}-1}\left| \varepsilon _k\right\rangle \left\langle \varepsilon _k\right| =\sum _{n=0}^{M_\mathrm{{b}}-1}|a_n|^2\left| \xi _n\right\rangle \left\langle \xi _n\right| \end{aligned}$$

(14)

where the coefficients $|a_n|^2$ in Eq. (14) can be obtained as follows:

$$\begin{aligned} |a_n|^2 = \frac{1}{M_\mathrm{{b}}}\sum _{k=0}^{M_\mathrm{{b}}-1}e^{-i\frac{2\pi }{M_\mathrm{{b}}}kn -\alpha ^2(1-\eta )\left( 1-e^{i\frac{2\pi }{M_\mathrm{{b}}}k}\right) }. \end{aligned}$$

(15)

Finally, the von Neumann entropy of density operator $\rho _{E|0}^{x}$ results

$$\begin{aligned} S(\rho _{E|0}^{x})=-\sum _{n}|a_n|^2\log _2(|a_n|^2). \end{aligned}$$

(16)

When transmitted data is 1, the density operator $\rho _{E|1}^{x}$ is given as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _{E|1}^{x}=\frac{1}{M_\mathrm{{b}}}\sum _{m=0}^{M_\mathrm{{b}}-1} \left| \varepsilon _{2m+1}\right\rangle \left\langle \varepsilon _{2m+1}\right| \\ \left| \varepsilon _{2m+1}\right\rangle =\left| \sqrt{(1-\eta )}\alpha e^{i\frac{\pi }{M_\mathrm{{b}}}(2m+1)}\right\rangle \end{array}\right. } \end{aligned}$$

(17)

where density matrix $\rho _{E|1}^{x}$ is Eve’s state conditioned on preparation of data bit state 1. The signal states are symmetric. So, the density operator $\rho _{E|1}^{x}$ can also be diagonalized by the orthogonal basis $\left| \zeta _{n}\right\rangle$ in the same way. The coefficients $|b_n|^2$ are given as follows (see “Appendix” for the diagonalization of density operator $\rho _{E|0}^{x}$ and $\rho _{E|1}^{x}$, respectively):

$$\begin{aligned} |b_n|^2 =\frac{1}{M_\mathrm{{b}}} \sum _{k=0}^{M_\mathrm{{b}}-1}e^{-i\frac{2\pi }{M_\mathrm{{b}}}kn -\alpha ^2(1-\eta )\left( 1-e^{i\frac{2\pi }{M_\mathrm{{b}}}k}\right) }. \end{aligned}$$

(18)

So, the von Neumann entropy of density operator $\rho _{E|1}^{x}$ is

$$\begin{aligned} S(\rho _{E|1}^{x}) = -\sum _{n}|b_n|^2\log _2(|b_n|^2). \end{aligned}$$

(19)

Next, we calculate the density operator $\rho _{E}^{x}$ for data. Because data 0 and 1 are random, the density operator $\rho _{E}^{x}$ is

$$\begin{aligned} \rho _{E}^{x} = \frac{1}{2}(\rho _{E|1}^{x}+\rho _{E|0}^{x}) =\frac{1}{2M_\mathrm{{b}}}\sum _{m=0}^{2M_\mathrm{{b}}-1}\left| \varepsilon _{m}\right\rangle \left\langle \varepsilon _{m}\right| \end{aligned}$$

(20)

where the density operator $\rho _E$ is the mixture of symmetrical pure states, and it can be diagonalized by the same way. We define that the orthogonal basis of density operator $\rho _E^{x}$ is given by $\left| \omega _n\right\rangle$. We have (see “Appendix” in detail)

$$\begin{aligned} |c_n|^2 = \frac{1}{2M_\mathrm{{b}}}\sum _{m=0}^{2M_\mathrm{{b}}-1}e^{-i\frac{\pi }{M_\mathrm{{b}}}mn -\alpha ^2(1-\eta )\left( 1-e^{i\frac{\pi }{M_\mathrm{{b}}}m}\right) }. \end{aligned}$$

(21)

The von Neumann entropy $S(\rho _{E}^{x})$ can be calculated as follows:

$$\begin{aligned} S(\rho _E^{x}) = -\sum _{n}|c_n|^2\log _2(|c_n|^2). \end{aligned}$$

(22)

Finally, by Eqs. (16), (19), and (22), the Holevo information of data x can be derived as follows:

$$\begin{aligned} I^{x}(A,E)&= S(\rho _E^{x})-\sum _k p_k S(\rho _{E|k}^{x})\nonumber \\&= -\sum _{n}|c_n|^2\log _2(|c_n|^2)+\frac{1}{2}\left( \sum _n|a_n|^2\log _2(|a_n|^2) +\sum _{n}|b_n|^2\log _2(|b_n|^2)\right) \nonumber \\&= -\sum _{n}|c_n|^2\log _2(|c_n|^2)+\sum _{n}|a_n|^2\log _2(|a_n|^2) \end{aligned}$$

(23)

where $p_k=\frac{1}{2}$.

According to Eqs. (9) and (23), the security capacity of data per bit, $R_\mathrm{{data}}$, under collective attacks is given as follows:

$$\begin{aligned} R_\mathrm{{data}}&= I^{x}(A,B)-I^{x}(A,E)-\delta ^{x} \nonumber \\&\le I^{x}(A,B)-I^{x}(A,E) \nonumber \\&= \log _2(2)+\int p(\phi _{\tilde{x},u})\sum _{\tilde{x}}p(\beta _{x,u} |\phi _{\tilde{x},u})\log _2(p(\beta _{x,u}|\phi _{\tilde{x},u})) \hbox {d}\beta \nonumber \\&\quad +\sum _n |c_n|^2\log _2(|c_n|^2)-\sum _n |a_n|^2\log _2(|a_n|^2). \end{aligned}$$

(24)

The transmitted signal states $\left| \phi _m\right\rangle$ also contain the information of the running key u. Thus, Eve can obtain information of the running key by intercepting the quantum channel. Next, the security capacity of running key $R_\mathrm{{key}}$ is derived. The information transmission of running key u is shown in Fig. 2. Bob has the same running key u with Alice. Thus, the mutual information between Alice and Bob on running key u is given as $I(A,B)^{u}=1$. (Here, the base-$M_\mathrm{{b}}$ is used for logarithmic operations. If we use base-2, it should be $I(A,B)^{u} =\log _2 M_\mathrm{{b}}$.) Thus, we only need to consider Eve’s information on running key u. When Eve has access to quantum channel, the density operator for different bases u is given as follows:

$$\begin{aligned} \rho _{E|u}^{u}=\frac{1}{2}(\left| \xi _{(0/1,u)}\right\rangle \left\langle \xi _{(0/1,u)}\right| +\left| \xi _{(1/0,u+M_\mathrm{{b}})}\right\rangle \left\langle \xi _{(1/0,u+M_\mathrm{{b}})}\right| ), u=0 \sim M_\mathrm{{b}}-1 \end{aligned}$$

(25)

where $\rho _{E|u}^{u}$ is the Eve’s state conditioned on preparation of running key u. The overlap between states $\left| \varepsilon _{(0/1,u)}\right\rangle$ and $\left| \varepsilon _{(1/0,u+M_\mathrm{{b}})}\right\rangle$ can be written as $\gamma ^2$ ($\gamma =e^{-\alpha _E^2}$). So, the $S(\rho _{E|u}^{u})$ can be expressed as follows:

$$\begin{aligned} S(\rho _{E|u}^{u}) = -\frac{1+\gamma ^2}{2}\log _{M_\mathrm{{b}}}\left( \frac{1+\gamma ^2}{2}\right) -\frac{1-\gamma ^2}{2}\log _{M_\mathrm{{b}}}\left( \frac{1-\gamma ^2}{2}\right) , \forall u = 0 \sim M_\mathrm{{b}}-1. \end{aligned}$$

(26)

The Holevo information of running key u is given as follows:

$$\begin{aligned} I^{u}(A,E)&= S(\rho _E^{u})-\sum _u p_u S(\rho _{E|u}^{u})\nonumber \\&= -\sum _{n}|c_n|^2\log _{M_\mathrm{{b}}}(|c_n|^2)+\frac{1+\gamma ^2}{2} \log _{M_\mathrm{{b}}}\left( \frac{1+\gamma ^2}{2}\right) \nonumber \\&\quad +\frac{1-\gamma ^2}{2}\log _{M_\mathrm{{b}}}\left( \frac{1-\gamma ^2}{2}\right) \end{aligned}$$

(27)

where $\rho _{E}^{u} = p_u\sum _u\rho _{E|u}^{u} = \rho _{E}^{x}$ and $p_u = \frac{1}{M_\mathrm{{b}}}$.

Finally, the security capacity of running key per bit, $R_\mathrm{{key}}$, under collective attacks is given as follows:

$$\begin{aligned} R_\mathrm{{key}}&= I^{u}(A,B)-I^{u}(A,E)-\delta ^{u} \nonumber \\&\le I^{u}(A,B)-I^{u}(A,E) \nonumber \\&= 1+\sum _{n}|c_n|^2\log _{M_\mathrm{{b}}}(|c_n|^2) -\frac{1+\gamma ^2}{2}\log _{M_\mathrm{{b}}}\left( \frac{1+\gamma ^2}{2}\right) \nonumber \\&\quad -\frac{1-\gamma ^2}{2}\log _{M_\mathrm{{b}}}\left( \frac{1-\gamma ^2}{2}\right) \end{aligned}$$

(28)

where the $|c_n|^2$ is calculated by Eq. (21). So, we can calculate the security capacity of data $R_\mathrm{{data}}$ and running key $R_\mathrm{{key}}$ by Eqs. (24) and (28), respectively. Then, we can obtain the systematic security capacity $R=\min \left\{ R_\mathrm{{data}},R_\mathrm{{key}}\right\}$ for QNSC system.

4 Results and discussion

Based on the above discussion, the security capacity of data $R_\mathrm{{data}}$, running key $R_\mathrm{{key}}$, and systematic security capacity R depends on the parameters $|a_n|^2$, $|b_n|^2$, $|c_n|^2$, and $\gamma$. These parameters are related to the mean photon number $\alpha ^2$, the number of bases $M_\mathrm{{b}}$, and transmission distance d (km). In this section, we present and discuss the security capacity of data $R_\mathrm{{data}}$ and running key $R_\mathrm{{key}}$, as a function of the transmission distance d, with the mean photon number $\alpha ^2$ and for different numbers of bases $M_\mathrm{{b}}$. Furthermore, systematic security capacity of QNSC R is also evaluated for given parameters. Here, the transmission distance between Alice and Bob is defined as d (km). The loss of quantum channel is fixed to 0.2 dB/km. There is no excess noise in the quantum channel, i.e., only quantum noise is considered in our analysis. We fixed the detection efficiency of the receiver, Bob, to be 100$\%$.

4.1 The security capacity of data $R_\mathrm{{data}}$

In Fig. 3, we report the security capacity of data $R_\mathrm{{data}}$, as a function of the transmission distance d (km), with different mean photon numbers $\alpha ^2$ and for three different numbers of bases $M_\mathrm{{b}}$. In Fig. 3a, $R_\mathrm{{data}}$ is close to 1 at the beginning and then exponentially drops for $\alpha ^2>1$ when the transmission distance d increases. Compared Fig. 3b with Fig. 3c, the $R_\mathrm{{data}}$ increases with the increases of the number of bases $M_\mathrm{{b}}$. So, the transmission distance d and security capacity $R_\mathrm{{data}}$ can be improved by increasing the number of bases $M_\mathrm{{b}}$. The number of bases $M_\mathrm{{b}}$ depends on the resolution of analog-to-digital converter (ADC) and digital-to-analog converter (DAC). Recently, an experiment with the maximum value of bases $2^{17}$ has been reported in paper [11]. The $R_\mathrm{{data}}$ exponentially drops for $\alpha ^2 \le 1$ when transmission distance d increases, in Fig. 3d. Due to the impact of quantum noise, Bob is not able to accurately measure received signal states $\left| \phi _m\right\rangle$ when the mean photon number $\alpha ^2$ is lower than 1 in Fig. 3a, d. Therefore, setting an appropriate photon $\alpha ^2$ can improve the security capacity $R_\mathrm{{data}}$.

Fig. 3

The security capacity $R_\mathrm{{data}}$ as a function of transmission distance d (km), with different mean photon numbers $\alpha ^2$ and for three different numbers of bases $M_\mathrm{{b}}$

Fig. 4

The security capacity $R_\mathrm{{data}}$ as a function of mean photon number $\alpha ^2$, with different bases $M_\mathrm{{b}}$ and for four different transmission distances d

As discussed above, the mean photon number $\alpha ^2$ are other main factor affecting security and transmission distance in QNSC system. So, we evaluate the security capacity $R_\mathrm{{data}}$ as a function of the mean photon number $\alpha ^2$, with different numbers of bases $M_\mathrm{{b}}$ and for four different distances d (km) in Fig. 4. As the mean photon number $\alpha ^2$ increases, security capacity $R_\mathrm{{data}}$ grows and then reaches the maximum in Fig. 4a. When the photons $\alpha ^2$ increase, the security capacity $R_\mathrm{{data}}$ decreases after reaching the maximum. Figure 4b, c shows that the maximum security capacity $R_\mathrm{{data}}$ increases as the number of bases $M_\mathrm{{b}}$ increases for fixed mean photon number $\alpha ^2$. However, with the increases in transmission distance between Alice and Bob d, the maximum security capacity of data $R_\mathrm{{data}}$ decreases by comparing Fig. 4b with Fig. 4c. In the case of a transmission distance d longer than 200 km and the number of bases is 127(255), the security capacity $R_\mathrm{{data}}$ linearly increases and then reaches maximum as photon number $\alpha ^2$ increases in Fig. 4c, d. The maximum security capacity of data $R_\mathrm{{data}}$ mainly depends on photon number $\alpha ^2$ when transmission distance d and resolution of ADC are fixed. Thus, it is important to set an appropriate input optical power in the optical fiber for the fixed distance d and the number of bases $M_\mathrm{{b}}$.

4.2 The security capacity of running key $R_\mathrm{{key}}$

Fig. 5

The security capacity $R_\mathrm{{key}}$ as a function of distances d (km), for different bases $M_\mathrm{{b}}$ and mean photon number $\alpha ^2$

Figure 5 shows that security capacity of running key $R_\mathrm{{key}}$ varies with different transmission distances d and the number of bases $M_\mathrm{{b}}$. As transmission distances d increase, the $R_\mathrm{{key}}$ decreases and then reaches minimum in Fig. 5a. When security capacity of running key $R_\mathrm{{key}}$ reaches minimum, the $R_\mathrm{{key}}$ remains almost constant as transmission distances d increase in Fig. 5a. Compared Fig. 5a with Fig. 5b, the minimum of $R_\mathrm{{key}}$ decreases as the distances d increase. Besides, the minimum value of $R_\mathrm{{key}}$ goes down when photon number $\alpha ^2$ increases in Fig. 5b. The relation between security capacity $R_\mathrm{{key}}$ and the number of bases $M_\mathrm{{b}}$ is reported for different transmission distances d in Fig. 5c, d. According to our model, the maximum security capacity of key $R_\mathrm{{key}}$ can be achieved by decreasing transmission distances d. Thus, we discuss the maximum $R_\mathrm{{key}}$ for $d = 1$km in Fig. 5c. As the number of photons $\alpha ^2$ increases, the maximum security capacity $R_\mathrm{{key}}$ decreases in Fig. 5c. However, maximum $R_\mathrm{{key}}$ increases with the increase of the the number of bases $M_\mathrm{{b}}$. For fixed distances d, the minimum $R_\mathrm{{key}}$ decreases as the photon $\alpha ^2$ increases in Fig. 5d. In order to work in longer distance, large photons $\alpha ^2$ are necessary. However, Eve can obtain more information when photons $\alpha ^2$ are larger. So, the trade-off between photon number $\alpha ^2$ and transmission distances d has to be considered for fixed bases $M_\mathrm{{b}}$ in deployment of QNSC system.

4.3 The systematic security capacity of QNSC system

Fig. 6

The systematic security capacity R as a function of mean photon number $\alpha ^2$, with different numbers of bases $M_\mathrm{{b}}$ and for four different distances d. The solid line is the security capacity of data $R_\mathrm{{data}}$. The dotted line is the security capacity of running key $R_\mathrm{{key}}$. Red line: $M_\mathrm{{b}}=15$; black line: $M_\mathrm{{b}}=31$; green line: $M_\mathrm{{b}}=63$; blue line: $M_\mathrm{{b}}=127$; pink line: $M_\mathrm{{b}}=255$

The systematic security capacity R is discussed as a function of mean photon number $\alpha ^2$, with four distances d and for different numbers of bases $M_\mathrm{{b}}$ in Fig. 6. The security capacity R of whole system is decided by the minimum between data capacity $R_\mathrm{{data}}$ and running key capacity $R_\mathrm{{key}}$, as shown in Eq.4. When the mean photon number $\alpha ^2$ is small, the security capacity R mainly depends on the security capacity of data $R_\mathrm{{data}}$ in Fig. 6a, b. However, with the increases of photons $\alpha ^2$, security capacity R is bounded by the security capacity of running key $R_\mathrm{{key}}$. Thus, when transmission distance d is fixed and shorter, the systematic security capacity R increases and then reaches the maximum as the photons $\alpha ^2$ increase. After reaching the maximum, systematic security capacity R decreases when the photons $\alpha ^2$ increase. For fixed bases $M_\mathrm{{b}}$, the maximum R decreases when transmission distances d increase, as seen by comparison of Fig. 6a, b. The security capacity R totally depends on the security of data $R_\mathrm{{data}}$ for fewer bases in Fig. 6c, d. In Fig. 6d, for $M_\mathrm{{b}} = 31$ and any mean photon number $\alpha ^2$, the sysmetric security capacity R depends on the security capacity of data $R_\mathrm{{data}}$ and the security capacity of data $R_\mathrm{{data}}$ is close to zero. So, the maximum transmission distance is no more than 300 km for given parameters.

Based on the above discussion, it is possible for QNSC system to provide the security by quantum noise even though Eve intercepts the system through collective attacks. The maximum security rate that QNSC can provide under collective attacks is associated with the number of photons $\alpha ^2$ and the number of bases $M_\mathrm{{b}}$. The number of bases $M_\mathrm{{b}}$ is determined by the resolution of ADC and DAC. Thus, in order to improve the security of QNSC, we can decrease the number of photons per signal state for fixed bases $M_\mathrm{{b}}$. However, decreasing photons $\alpha ^2$ will decrease the transmission distance d of QNSC system. We have to consider the trade-off between security rate and transmission distance in deployment of QNSC system. The maximum security capacity can be obtained when the correlation between running key u is zero. However, to obtain higher transmission rate, the key expansion has to be used for QNSC system in practice. Due to weak correlation between running key u from key expansion, the maximum security capacity for data $R_\mathrm{{data}}$, running key $R_\mathrm{{key}}$, and whole system R decreases. However, if the $\delta$ is larger than whole system R, QNSC system will be unsafe under collective attacks. Thus, our analysis also provides the reference to design of key expansion in QNSC system.

5 Conclusions

This paper evaluates the security performance of QNSC against collective attacks. We derive the maximum secure rate of data x and running key u under such hypothesis. The maximum security capacity for data x, running key u, and whole system is discussed for different parameters, such as distance d, mean photon number $\alpha ^{2}$, and the number of bases $M_\mathrm{{b}}$. The results show that QNSC system can achieve nonzero secure rate even if Eve intercepts useful information by collective attacks when data transmission distance is no more than 300 km for the number of bases $M_\mathrm{{b}}=31$ and any mean photon number $\alpha ^2$. For shorter distance, security capacity of the whole system is mainly bounded by the security capacity of the running key. However, the security of the system is limited by security of data when transmission distance is longer. So, protecting the security of data from eavesdropping is important for longer distance in QNSC system. Our work will pave the way for a better security analysis of the Y-00 protocol.

Appendix: Symmetric states and diagonalization of symmetric coherent states in QNSC

In this section, we derive Eqs. (15), (18), and (21). First, we simply introduce the definition of symmetric states. A set of quantum states $\left| \psi _j\right\rangle$ spanning a Hilbert space H is symmetric if there exists a unitary transformation $\hat{U}$ on such that [29, 30]

$$\begin{aligned} \left| \phi _j\right\rangle&= \hat{U}\left| \phi _j\right\rangle = \hat{U}^j\left| \phi _0\right\rangle \nonumber \\ \left| \phi _0\right\rangle&= \hat{U}\left| \phi _{N-1}\right\rangle \nonumber \\ \hat{U}^N&= I. \end{aligned}$$

(29)

The unitary operator $\hat{U}$ can be expanded as follows:

$$\begin{aligned} \hat{U}=\sum _{k=0}^{N-1}e^{i\theta _k} \left| \gamma _k\right\rangle \left\langle \gamma _k\right| \end{aligned}$$

(30)

where $\left\langle \gamma _k|\gamma _{k'}\right\rangle =\delta _{kk'}$.

According to Eqs. (29) and (30), the real angles $\theta _k$ are given by

$$\begin{aligned} \theta _k=\frac{2\pi f_k}{N} \end{aligned}$$

(31)

where $f_k$ is an integer satisfying $0\le f_k\le n-1$.

Clearly, we can expand $\left| \phi _0\right\rangle$ as

$$\begin{aligned} {\left\{ \begin{array}{ll} \left| \phi _0\right\rangle = \sum _{k}c_k\left| \gamma _k\right\rangle \\ \sum _k |c_k|^2=1. \end{array}\right. } \end{aligned}$$

(32)

By Eqs. (31) and (32), the any states $\left| \phi _j\right\rangle$ are given by

$$\begin{aligned} \left| \phi _j\right\rangle = \sum _{k=0}^{N-1}c_k e^{\frac{2\pi f_k ij}{N}}\left| \gamma _k\right\rangle . \end{aligned}$$

(33)

The quantum states $\left| \phi _j\right\rangle$ are the linear independence. So, all of the coefficients $c_k$ are nonzero.

$$\begin{aligned} \frac{1}{N}\sum _{j=0}^{N-1}e^{\frac{-2\pi r ij}{N}}\left| \phi _j\right\rangle =\sum _{k=0}^{N-1}c_k\delta _{rf_k}\left| \gamma _k\right\rangle . \end{aligned}$$

(34)

According to linear independence, we have

$$\begin{aligned} f_k = k. \end{aligned}$$

(35)

Based on the definition of symmetric states, the signal states of QNSC in Eq. (12) are expressed as

$$\begin{aligned} \left| \varepsilon _k\right\rangle =\left| \sqrt{(1-\eta )}\alpha e^{i\frac{2\pi }{M_\mathrm{{b}}}k}\right\rangle = \sum _{n=0}^{M_\mathrm{{b}}-1}a_n e^{i\frac{2\pi }{M_\mathrm{{b}}}kn}\left| \xi _n\right\rangle , \ k\in \left\{ 0,1,...,M_\mathrm{{b}}-1\right\} \end{aligned}$$

(36)

where $\left| \xi _n\right\rangle$ is orthogonal basis in Hilbert space. The coefficients $a_n$ satisfy $\sum _{n}|a_n|^2=1$. The density matrix in Eq. (14) can be diagonalized by the orthogonal basis $\left| \xi _n\right\rangle$.

$$\begin{aligned} \rho _{E|0}^{x} = \frac{1}{M_\mathrm{{b}}}\sum _{k=0}^{M_\mathrm{{b}}-1} \left| \varepsilon _k\right\rangle \left\langle \varepsilon _k\right| =\sum _{n=0}^{M_\mathrm{{b}}-1}|a_n|^2\left| \xi _n\right\rangle \left\langle \xi _n\right| . \end{aligned}$$

(37)

The von Neumann entropy of density matrix $\rho _{E|0}^{x}$ is related to its eigenvalues. Thus, we have to calculate the value of $|a_n|^2$. The coefficients $|a_n|^2$ are derived by

$$\begin{aligned} \left\langle \varepsilon _0|\varepsilon _k\right\rangle =\sum _{n=0}^{M_\mathrm{{b}}-1}e^{i\frac{2\pi }{M_\mathrm{{b}}}kn}|a_n|^2. \end{aligned}$$

(38)

By solving Eq. (38) for different values k, we find that

$$\begin{aligned} |a_n|^2 = \frac{1}{M_\mathrm{{b}}}\sum _{k=0}^{M_\mathrm{{b}}-1}e^{-i\frac{2\pi }{M_\mathrm{{b}}}kn -\alpha ^2(1-\eta )\left( 1-e^{i\frac{2\pi }{M_\mathrm{{b}}}k}\right) }. \end{aligned}$$

(39)

Finally, the von Neumann entropy of density operator $\rho _{E|0}^{x}$ for data can be calculated as follows:

$$\begin{aligned} S(\rho _{E|0}^{x}) = -\sum _n |a_n|^2\log _2(|a_n|^2). \end{aligned}$$

(40)

When transmitted data x is 1, signal states are symmetric. So, based on the orthogonal basis $\left| \zeta _n\right\rangle$, density matrix $\rho _{E|1}^{x}$ can be expressed as follows:

$$\begin{aligned} \rho _{E|1}^{x} = \frac{1}{M_\mathrm{{b}}}\sum _{k=0}^{M_\mathrm{{b}}-1}\left| \varepsilon _k\right\rangle \left\langle \varepsilon _k\right| = \sum _{n=0}^{M_\mathrm{{b}}-1}|b_n|^2 \left| \zeta _n\right\rangle \left\langle \zeta _n\right| \end{aligned}$$

(41)

where $\left| \varepsilon _k\right\rangle = \left| \sqrt{(1-\eta )} \alpha e^{i\frac{\pi }{M_\mathrm{{b}}}(2k+1)}\right\rangle$. So, the density matrix $\rho _{E|1}^{x}$ can be diagonalized by the orthogonal basis $\left| \zeta _n\right\rangle$ by the same way. The coefficients $|b_n|^2$ are given as follows:

$$\begin{aligned} \left\langle \varepsilon _0|\varepsilon _k\right\rangle =\sum _{n=0}^{M_\mathrm{{b}}-1}e^{i\frac{2\pi }{M_\mathrm{{b}}}kn}|b_n|^2. \end{aligned}$$

(42)

So, we have

$$\begin{aligned} |b_n|^2 = \frac{1}{M_\mathrm{{b}}}\sum _{k=0}^{M_\mathrm{{b}}-1}e^{-i\frac{2\pi }{M_\mathrm{{b}}}kn -\alpha ^2(1-\eta )\left( 1-e^{i\frac{2\pi }{M_\mathrm{{b}}}k}\right) } \end{aligned}$$

(43)

The signal states are mixture of Alice’s preparation states with equal probability. So, the density operator $\rho _E$ is given as follows:

$$\begin{aligned} \rho _{E}^{x}&= \frac{1}{2}(\rho _{E|0}^{x}+\rho _{E|1}^{x})\nonumber \\&= \frac{1}{2}\left( \frac{1}{M_\mathrm{{b}}}\sum _{k=0}^{M_\mathrm{{b}}-1}\left| \varepsilon _{2k}\right\rangle \left\langle \varepsilon _{2k}\right| +\frac{1}{M_\mathrm{{b}}}\sum _{k=0}^{M_\mathrm{{b}}-1} \left| \varepsilon _{2k}\right\rangle \left\langle \varepsilon _{2k}\right| \right) \nonumber \\&= \frac{1}{2M_\mathrm{{b}}}\sum _{k=0}^{2M_\mathrm{{b}}-1}\left| \varepsilon _{k} \right\rangle \left\langle \varepsilon _{k}\right| \end{aligned}$$

(44)

where $\left| \varepsilon _{k} \right\rangle =\left| \sqrt{(1-\eta )} \alpha e^{i\frac{\pi }{M_\mathrm{{b}}}k}\right\rangle$. By Eq. (44), the density matrix $\rho _{E}^{x}$ is also the mixture of symmetric states. Applying property of symmetric states, it can be

$$\begin{aligned} \rho _{E}^{x}&= \frac{1}{2M_\mathrm{{b}}}\sum _{k=0}^{2M_\mathrm{{b}}-1} \left| \varepsilon _k\right\rangle \left\langle \varepsilon _k\right| \nonumber \\&= \sum _{k=0}^{2M_\mathrm{{b}}-1}|c_n|^2\left| \omega _n\right\rangle \left\langle \omega _n\right| \end{aligned}$$

(45)

where $\left| \omega _n\right\rangle$ is the orthogonal basis in the states space.

By the same way, the coefficients $|c_n|^2$ are given as follows:

$$\begin{aligned} \left\langle \varepsilon _0|\varepsilon _k\right\rangle =\sum _{n=0}^{2M_\mathrm{{b}}-1}e^{i\frac{\pi }{M_\mathrm{{b}}}kn}|c_n|^2. \end{aligned}$$

(46)

So, the coefficients $|c_n|^2$ can be derived

$$\begin{aligned} |c_n|^2 = \frac{1}{2M_\mathrm{{b}}}\sum _{m=0}^{2M_\mathrm{{b}}-1}e^{-i\frac{\pi }{M_\mathrm{{b}}}mn -\alpha ^2(1-\eta )\left( 1-e^{i\frac{\pi }{M_\mathrm{{b}}}m}\right) }. \end{aligned}$$

(47)