Public-key quantum signature for classical messages without third-party verification

Abstract

Based on quantum asymmetric cryptosystem, a public-key quantum signature for classical messages is proposed. In our scheme, the private key is randomly chosen by signer, and the public key is generated by the trusted key generator using the quantum one-way function. The signer signs a message with the private key, while the verifier can use the public key to verify the quantum signature without the help of third party. The signer’s key pair can be reused. Hence, our scheme can simplify the key management of the quantum signature system. Security analysis results show that the proposed scheme satisfies unforgeability and non-repudiation. All the algorithms in our scheme are public. Compared to similar schemes, ours is relatively more secure and can be easily applied to practical scenarios.

Appendices

Appendix A: Review of Chen et al.’s public-key quantum signature scheme

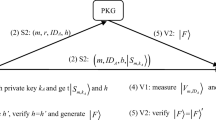
Chen et al.’s public-key quantum signature scheme [23] includes three steps.

i. Key generation phase

The signer’s public key $k_{p u b}$ is derived from her personal public identity information and the PKG generates the private key $k_{p r i}$ by the following steps:

(1) The signer and PKG share $k_{A T}$ as their shared key in advance.

(2) PKG secretly selects a classical one-way function G and a random number $k_{r}$.

(3) PKG calculates the private key $k_{p r i}:=G\left( k_{p u b}\right) \oplus k_{r}$ and transmits $E_{k_{A T}}\left( k_{p r i}\right)$ to the signer.

ii. Signature phase

The signer generates the quantum signature on the message $m=(m_1, m_2, \ldots , m_n)$ by following steps:

(1) Choose two random strings $s=\left( s_{1}, s_{2}, \ldots , s_{n}\right)$ and $t=\left( t_{1}, t_{2}, \ldots , t_{n}\right)$.

(2) Generate $|\phi \rangle _{s_{l}, t_{l} \oplus m_{l}}=H^{s_{l}} U_{\frac{\pi }{4}} H^{t_{l} \oplus m_{l}}|0\rangle$ and $|\varphi \rangle _{s_{l}, t_{l} \oplus m_{l}, m_{l}}=Y^{m_{l}}|\phi \rangle _{s_{l}, t_{l} \oplus m_{l}}, \quad$ where $l=$ $1,2, \ldots , n$ and

$$\begin{aligned} H=\frac{\sqrt{2}}{2}\left( \begin{array}{cc} 1 &{} 1 \\ 1 &{} -1 \end{array}\right) , \quad U_{\frac{\pi }{4}}=\frac{\sqrt{2}}{2}\left( \begin{array}{cc} 1 &{} -1 \\ 1 &{} 1 \end{array}\right) , \quad Y=\left( \begin{array}{cc} 0 &{} -i \\ i &{} 0 \end{array}\right) \end{aligned}$$

Let $|\phi \rangle _{s, t \oplus m}=\otimes _{l=1}^{n}|\phi \rangle _{s_{l}, t_{l} \oplus m_{l}}$ and $|\varphi \rangle _{s, t \oplus m, m}=\otimes _{l=1}^{n}|\varphi \rangle _{s_{l}, t_{l} \oplus m_{l}, m_{l}} .$

(3) Generate signature $|S\rangle _{k_{p r i}, m}=\otimes _{l=1}^{n}|S\rangle _{k_{p r i_{l}}, m_{l}}=\otimes _{l=1}^{n} H^{k_{p u b_{l}} \oplus k_{p r i_{l}}}|\varphi \rangle _{s_{l}, t_{l} \oplus m_{l}, m_{l}} .$

(4) Calculate $|P\rangle :=H^{k_{p r i}}|\phi \rangle _{s, t \oplus m} \in \{|0\rangle ,|1\rangle ,|+\rangle ,|-\rangle \}^{n}$, denote by $B_{P}=Basis(|P\rangle )$ the basis of each qubit state in $|P\rangle$ and denote classical $2 \mathrm {n}$-bit P for the n-qubit state $|P\rangle$ by $|0\rangle$ encoded into $01,|1\rangle$ encoded into $00,|+\rangle$ encoded into 10 and $|-\rangle$ encoded into 11 .

(5) Generate uw copies of quantum digest $|F\rangle :=|F(t\Vert m\Vert P \Vert t s)\rangle$ with the public quantum one-way function F, where u indicates the maximum number of verifiers, w is some safety parameter threshold and ts represents timestamp.

(6) Send quantum digest $E_{k_{A T}}\left( t s, \otimes _{l=1}^{u w}|F\rangle \right)$ to PKG and signature $\left( t s, m, B_{P},|S\rangle _{k_{\text{ pri } }, m}\right)$ to the verifier.

iii. Verification phase

The verifier verifies the quantum signature $\left( t s, m, B_{P},|S\rangle _{k_{p r i}, m}\right)$ by the following steps.

(1) Generate $|V\rangle _{k_{p u b, s}}:=H^{k}{ }_{p u b}|S\rangle _{k_{p r i}, m}$ and $|V\rangle _{m, k_{p u b, s}}:=Y^{m}|V\rangle _{k_{p u b, s}}$

(2) Measure $|V\rangle _{m, k_{p u b}, S}$ according to $B_{P}$ and get the result $|Q\rangle$, which is converted to set of classical 2-bit string denoted as $Q \in \{00,01,10,11\}^{n} .$

(3) Infer the random t from Q and generate w copies of quantum digest $|F\rangle ^{\prime }:=|F(t\Vert m\Vert Q \Vert$ $t s)\rangle$ with the public quantum one-way function F.

(4) Gain $\left( t s, \otimes _{l=1}^{w}|F\rangle \right)$ from $\mathrm {PKG}$ and compare $|F\rangle ^{\prime }$ with $|F\rangle$ by SWAP test. If the number $w^{\prime }$ of $|F\rangle ^{\prime }=|F\rangle$ is greater than the given a security threshold $w_{0}$, the verifier accepts the signature. Otherwise, he rejects the signature.

Appendix B: Forgery attack

In this section, we will prove that the scheme in [23] is insecure against forgery attack. That is, a malicious attacker can forge Alice’s signature by verifying the legitimate signature.

Since the signature

$$\begin{aligned} \vert {S}\rangle _{k_{pri},m}&=\otimes _{l=1}^nH^{k_{{pub}_l}\oplus k_{{pri}_l}}\vert \varphi \rangle _{s_l,t_l\oplus m_l,m_l} \nonumber \\&=\otimes _{l=1}^nH^{k_{{pub}_l}\bigoplus k_{{pri}_l}}\left( i^{m_l\left( 3+2s_l\right) }\vert \phi \rangle _{s_l\oplus m_l,t_l}\right) \nonumber \\&=\otimes _{l=1}^ni^{m_l\left( 3+2s_l\right) }\vert \phi \rangle _{k_{{pub}_l}\oplus k_{{pri}_l}\oplus s_l\oplus m_l,t_l} \nonumber \\&=\otimes _{l=1}^ni^{m_l\left( 3+2s_l\right) }H^{k_{{pub}_l}\oplus k_{{pri}_l}\oplus s_l\oplus m_l}U_\frac{\pi }{4}H^{t_l}\vert 0\rangle \nonumber \\&=i^{m\left( 3+2s\right) }H^{k_{pub}\oplus k_{pri}\oplus s\oplus m}U_\frac{\pi }{4}H^t\vert 0\rangle \end{aligned}$$

(B1)

it follows that the attacker does not need to obtain the private key $k_{p r i}$, as long as he/she learns about $k_{p r i} \oplus s$ and t, he/she can learn about $H^{k_{p u b} \oplus k_{p r i} \oplus s \oplus m} U_{\frac{\pi }{4}} H^{t}$ so as to forge a quantum signature $|S\rangle _{k_{p r i}, m} .$

First, the attacker can intercept $\left( t s, m, B_{P},|S\rangle _{k_{p r i}, m}\right)$ and generate $|V\rangle _{m, k_{p u b}, s}$,

$$\begin{aligned} \vert {V}\rangle _{{m,k}_{pub},s}&=Y^m\vert {V}\rangle _{k_{pub},S} \nonumber \\&=Y^m\left( H^{k_{pub}}\vert {S}\rangle _{k_{pri},m}\right) \nonumber \\&=\otimes _{l=1}^ni^{m_l\left( 3+2s_l\right) }Y^{m_l}\left( H^{k_{{pub}_l}}\vert {S}\rangle _{k_{{pri}_l},m_l}\right) \nonumber \\&=\otimes _{l=1}^ni^{m_l\left( 3+2s_l\right) }Y^{m_l}\left( H^{k_{{pub}_l}}\vert \phi \rangle _{k_{{pub}_l}\oplus k_{{pri}_l}\oplus s_l\oplus m_l,t_l}\right) \nonumber \\&=\otimes _{l=1}^ni^{m_l\left( 3+2s_l\right) }Y^{m_l}\vert \phi \rangle _{k_{{pri}_l}\oplus s_l\oplus m_l,t_l}\nonumber \\&=\otimes _{l=1}^ni^{m_l\left( 3+2s_l\right) }i^{m_l\left( 3+2\left( k_{{pri}_l}+s_l+m_l\right) \right) }\vert \phi \rangle _{k_{{pri}_l}\oplus s_l\oplus m_l,t_l} \nonumber \\&=\otimes _{l=1}^ni^{m_l\left( 6+2k_{{pri}_l}+4s_l+2m_l\right) }H^{k_{{pri}_l}\oplus s_l\oplus m_l}U_\frac{\pi }{4}H^{t_l}\vert 0\rangle \nonumber \\&=i^{m\left( 6+2k_{pri}+4s+2m\right) }H^{k_{pri}\oplus s\oplus m}U_\frac{\pi }{4}H^{t}\vert 0\rangle \in \left\{ \vert 0\rangle ,\vert 1\rangle ,\vert +\rangle ,\vert -\rangle \right\} ^n. \end{aligned}$$

(B2)

Then, the attacker measures $|V\rangle _{m, k_{p u b, s}}$ according to $B_{P}$ so that he/she can infer the random $k_{p r i} \oplus s$ and t. Hence, the attacker can forge the signature $|S\rangle _{k_{p r i}, m}$ for the original message m.

Note that the attacker does not need to disturb the channel between the signer and PKG. According to the verification phase, it is easy to prove that the forgery can pass the verification. Therefore, the public-key quantum signature in [23] is insecure against the forgery attack.

Moreover, because a malicious attacker can forge the signer’s signature, the signer can deny his/her valid quantum signature and claim that the signature is forged by another party. Therefore, the scheme in [23] is not secure against repudiation, either.