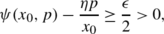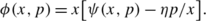On scheduling a multiclass queue with abandonments under general delay costs

Abstract

We consider a multiclass queueing system with abandonments and general delay costs. A system manager makes dynamic scheduling decisions to minimize long-run average delay and abandonment costs. We consider the three types of delay cost: (i) linear, (ii) convex, and (iii) convex–concave, where the last one corresponds to settings where customers may have a particular deadline in mind but once that deadline passes there is increasingly little difference in the added delay. The dynamic control problem for the queueing system is not tractable analytically. Therefore, we consider the system in the conventional heavy traffic regime and study the approximating Brownian control problem (BCP). We observe that the approximating BCP does not admit a pathwise solution due to abandonments. In particular, the celebrated cμ rule and its extension, the generalized cμ rule, which is asymptotically optimal under convex delay costs with no abandonments, are not optimal in this case. Consequently, we solve the associated Bellman equation, which yields a dynamic index policy (derived from the value function) as the optimal control for the approximating BCP. Interpreting that control in the context of the original queueing system, we propose practical policies for each of the three cases considered and demonstrate their effectiveness through a simulation study.

Appendices

Appendix A: Formal derivation of the approximating Brownian control problem

To facilitate the derivation of the Brownian control problem, note by the functional strong approximations, cf. [17], that

(60)

(61)

where $\hat { B}_{ k}$, $\tilde { B}_{ k}$for (k=1,…,K) are independent standard Brownian motions and $o(\sqrt{ n})/\sqrt { n} \rightarrow0$ as n→∞.

Also, define the following scaled quantities for n≥0 and t≥0:

The following observation facilitates our derivation as well: For k=1,…,K

(62)

The strong law of large numbers for Poisson processes implies that $N_{ k}(\sqrt{ n} t)/\allowbreak \sqrt{ n} \rightarrow t$ as n→∞ almost surely for t≥0 and k=1,…,K. Therefore, we will replace $\hat { \varGamma }_{ k}^{ n}( t)$ by $\int_{0}^{ t} \gamma _{ k} \hat { Q}_{ k}^{ n}(s)\,ds$ in deriving the approximating Brownian control problem.

Then substituting (18), (60) and (61) into (2) and replacing $\hat { \varGamma }_{ k}^{ n}( t)$ by $\int_{0}^{ t} \gamma _{ k} \hat { Q}_{ k}^{ n}(s)\,ds$ in (2), we arrive at the following:

(63)

where B _k is a standard Brownian motion. Similarly, it follows from (18) that

(64)

and (7) and (9) translate into the following under scaling:

(65)

(66)

Also, using (16), the snapshot principle (17) and substituting $\int_{0}^{ t} \gamma _{ k} \hat { Q}_{ k}^{ n}(s)\,ds$ for $\hat { \varGamma }_{ k}^{ n}( t)$, the scaled cost function is approximated by

(67)

Moreover, it follows from (4) and (62)–(64) that

(68)

where $B( t)= \sum _{ k=1}^{ K}m_{ k} B_{ k}( t)$ for t≥0.

We arrive at the approximating Brownian control problem by passing to the limit in (63)–(68) formally. Namely, assuming $\hat{Y}^{ n}\rightarrow Y$ as n→∞, we conclude that $\hat{ Q}^{ n}\rightarrow Q$, $\hat{ W}^{ n}\rightarrow W$ and $\hat{ H}^{ n}\rightarrow H$ as n→∞, where

(69)

(70)

(71)

(72)

(73)

(74)

and the approximating Brownian control problem can be stated as

Appendix B: Auxiliary results and proofs of technical results

Proof of Lemma 1

It is immediate from (38) that ψ(x,v) is decreasing in v. Also note from (31)–(32) that

(75)

where the minimand is continuous in x,y, and v (for x>0; and defining ψ(0,v)=0 extends continuity everywhere). Consider two pairs (x ₁,y ₁) and (x ₂,y ₂), and assume without loss of generality that ψ(x ₁,v ₁)≤ψ(x ₂,v ₂). Clearly, there exist y ¹,y ² such that

Then it follows from (75) that

Thus,

from which the continuity of ψ follows since g,θ are continuous.

For the Lipschitz continuity of ψ in v, we can repeat the same steps with x ₁=x ₂=x, which gives

 □

Proof of Lemma 2

Let X(t) be the reflected Brownian motion on [0,∞) with drift rate −η<0 and infinitesimal variance σ ². For any admissible policy, we have

because f is monotone and X(t) is stochastically larger than W ^∗(t), where the latter assertion follows because there are no abandonments involved in the evolution of process X(⋅). Therefore, it suffices to show that

To establish this, recall that $\bar {p}< \infty$. Then since v ^∗(x) is increasing with $\lim_{x\rightarrow\infty} v^{*}(x) = \bar {p}$, we conclude that $v^{*}(x) \leq \bar {p}$ for all x. Thus, $f(x) \leq \bar {p}x$. Then

But we also have (see [23]) that

Therefore, $\mathbb{E}[f(X(t))]/ t\rightarrow0$ as t→∞. □

The following lemma is immediate from the convexity of h _k (for k=1,…,K) and establishes that ψ is monotone.

Lemma 3

ψ(x,p) is strictly increasing in x in the cases of convex or convex–concave delay costs, whereas it is independent of x in the linear delay cost case.

Lemma 4

$\bar {p}= \min_{k} \lim_{x\rightarrow\infty} ( h_{ k}'(x) + a_{ k} \gamma _{ k}) / \gamma _{ k}m_{ k}< \infty$.

Proof of Lemma 4

For notational convenience, let $\alpha= \min_{k} \lim_{x\rightarrow\infty} ( h_{ k}'(x) + a_{ k} \gamma _{ k}) / \gamma _{ k}m_{ k}$. For any p>α, it is easy to see that ψ(x,p)<0. Thus $\bar {p}\leq p$ for all p>α, which implies $\bar {p}\leq\alpha$. Next, we argue that $\bar {p}\geq\alpha- \epsilon$ for ϵ>0. To this end, fix ϵ>0, then there exists x ₀ such that

Thus ψ(x,α−ϵ)>0 so that $\bar {p}\geq\alpha- \epsilon$ for ϵ>0, from which we conclude that $\bar {p}\geq\alpha$. □

Lemma 5

The following hold:

• (i) $\underline {x}(p)< \infty$ for $p \in(0, \bar {p})$.

• (ii) $\psi( \underline {x}(p),p) = \eta p / \underline {x}(p)$.

• (iii) $\underline {x}(p)$ is strictly increasing in p.

• (iv) $\lim_{p\rightarrow \bar {p}} \underline {x}(p)= \infty$.

• (v) ψ(x,p)>ηp/x for $x > \underline {x}(p)$.

• (vi) ϕ(x,p) is strictly increasing in x for $x > \underline {x}(p)$.

Proof of Lemma 5

Part (i):

Since $p < \bar {p}$ and ψ is monotone in x, there exist ϵ>0 sufficiently small and x ₁<∞ sufficiently large such that ψ(x,p)≥ϵ for all x≥x ₁. Similarly, there exists x ₂<∞ sufficiently large such that ηp/x≤ϵ/2 for all x≥x ₂. Then letting x ₀=max{x ₁,x ₂}<∞,

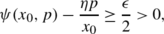
and thus, $\underline {x}(p)< x_{0}< \infty$ by the monotonicity of ψ(x,p) in x.

Part (ii):

Suppose not. Then $\psi( \underline {x}(p),p) > \eta p / \underline {x}(p)$ which contradicts the fact that $\underline {x}(p)$ is the infimum since $\psi( \underline {x}(p)- \epsilon, p) > \eta p / ( \underline {x}(p)- \epsilon)$ for ϵ>0 sufficiently small.

Part (iii):

This is clear from the fact that ψ(x,p)−ηp/x is strictly increasing in x and strictly decreasing in p.

Part (iv):

Suppose not. Then there exists M>0 such that $\underline {x}(p)\leq M$ for all $p < \bar {p}$, which implies $\psi(M, \bar {p}) \geq\eta \bar {p}/M$. But then $\psi(2M, \bar {p}) - \eta \bar {p}/ (2M) > 0$ because ψ(x,p)−ηp/x is strictly increasing in x. Thus, we conclude that $\psi(2M, \bar {p}+ \epsilon) > \eta( \bar {p}+ \epsilon)/ 2M$ for ϵ>0 sufficiently small, which contradicts the fact that $\bar {p}$ is the supremum of p>0 such that lim _x→∞ ψ(x,p)>0. Therefore, $\underline {x}(p)\rightarrow\infty$ as $p \rightarrow \bar {p}$.

Part (v):

This follows from part (ii) and the fact that ψ(x,p)−ηp/x is strictly increasing in x.

Part (vi):

Recall that

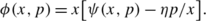
Then the result follows from the facts that ψ(x,p)−ηp/x≥0 for $x \geq \underline {x}(p)$ and that it is strictly increasing in x.

 □

Lemma 6

Let x ₂>x ₁>0 and $p \in(0, \bar{p})$. Suppose either ϕ(x ₂,p)>0 or ϕ(x ₁,p)>0. Then ϕ(x ₂,p)>ϕ(x ₁,p).

Proof of Lemma 6

First, assume ϕ(x ₂,p)>0 and recall that

let $y_{k}^{*}$ be the minimizer of the right-hand side. Then

where the first term on the right-hand side is positive because ϕ(x ₂,p)>0. Thus, we conclude that

where the first inequality follows since the first term on the right-hand side is positive, the second inequality follows from convexity of h _k (⋅) and that h _k (0)=0, and the third one follows from the min operation.

Alternatively, assume ϕ(x ₁,p)>0. Then note that

where the first inequality follows from convexity of h _k (⋅) and that h _k (0)=0, whereas the next inequality follows since the first term on the right-hand side is positive and x ₂/x ₁>1. □

Lemma 7

Let v be the unique solution to $\mathrm{IVP}( \hat {x})$ for $\hat {x}> \underline {x}(p)$ and $p \in(0, \bar{p})$. Suppose there exists $x^{*} \in[0, \hat {x}]$ such that v′(x ^∗)=0. Then

Proof of Lemma 7

Recall that ϕ(x,v)=xψ(x,v)−ηp. Since v′(x ^∗)=0, it follows from (45) that $\phi(x^{*}, v(x^{*})) = \phi( \hat {x}, p) > 0$, which implies ψ(x ^∗,v(x ^∗))>ηv(x ^∗)/x ^∗>0. Then for x>x ^∗, we have ψ(x,v(x ^∗))≥ψ(x ^∗,v(x ^∗))>0 by Lemma 3. Therefore for x>x ^∗,

 □

Proof of Proposition 2

First let $( q, \hat { L})$ be an admissible policy for the workload problem with the associated workload process W, and define $\hat{ Q}( t) = q( t, W( t))$. It is straightforward to check that ($\hat{ Q}$, $\hat { L}$) is an admissible policy for the reduced Brownian control problem; and the two policies have the same cost. Next, let ($\hat{ Q}$, $\hat { L}$) be an admissible policy for the reduced BCP. Then choose the workload configuration function q such that q(t,W(t))=Q(t) for t≥0. (Recall that we allow the workload configuration function q to depend on the sample path.) Clearly, $( q, \hat { L})$ is an admissible policy for the workload problem, and its cost is less than or equal to that of the policy ($\hat{ Q}$, $\hat { L}$) for the reduced Brownian control problem. □

Proof of Proposition 3

Part (i). It follows from Lemma 1, the fact that ϕ(x,v)=xψ(x,v)−ηv, and Picard’s iteration arguments; see pages 89–98 of Boyce and DiPrima [13], that there exists δ>0 such that we have a unique continuously differentiable solution $v_{ \hat {x}}$ on [0,δ]. This result can be extended to the entire interval [0,K] for all K>0 (and hence to [0,∞)) by mimicking the arguments on page 192 of Mandl [43].

Part (ii). Let $\hat {x}_{2} > \hat {x}_{1} > \underline {x}(p)$. We want to show that $v_{ \hat {x}_{2}}(x)>v_{ \hat {x}_{1}}(x)$ for all x>0, where

(76)

Suppose that $v_{ \hat {x}_{1}}(x) \geq v_{ \hat {x}_{2}}(x)$ for some x>0. Let $x^{*} = \inf\{ x\geq0 : v_{ \hat {x}_{1}}(x) \geq v_{ \hat {x}_{2}}(x) \}$. If x ^∗>0, then our hypothesis and the continuity of $v_{ \hat {x}_{1}}$ and $v_{ \hat {x}_{2}}$ guarantee that $v_{ \hat {x}_{1}}(x^{*})=v_{ \hat {x}_{2}}(x^{*})$, and that $v_{ \hat {x}_{1}}(x) \leq v_{ \hat {x}_{2}}(x)$ on [0,x ^∗]. Then it follows from (76) that

Since ϕ(s,⋅) is nonincreasing (by Lemma 1), and $\phi ( \hat {x}_{2}, p) > \phi( \hat {x}_{1}, p)$ (by part (vi)) of Lemma 5), we have

which is a contradiction.

If x ^∗=0, then there exists a sequence {x _n } such that x _n ↓0 as n→∞ and $v_{ \hat {x}_{1}}(x_{n}) \geq v_{ \hat {x}_{2}}(x_{n})$. In particular,

Because $v_{ \hat {x}_{1}}(0) = v_{ \hat {x}_{2}}(0)$, taking the limit as n→∞ gives $v'_{ \hat {x}_{2}}(0) \leq v'_{ \hat {x}_{1}}(0)$, which in turn implies $\phi( \hat {x}_{2}, p) \leq\phi( \hat {x}_{1}, p)$ by (45), contradicting the fact that $\hat {x}_{2} > \hat {x}_{1} > \underline {x}(p)$ by part (vi) of Lemma 5.

Therefore, $\hat {x}_{2} > \hat {x}_{1} > \underline {x}(p)$ implies $v_{ \hat {x}_{1}}(x)<v_{ \hat {x}_{2}}(x)$ for all x>0.

Part (iii) To show that $v_{ \hat {x}}$ strictly increases to its maximum on $[0, \hat {x}]$, we proceed in two steps: The first step is to show that $v_{ \hat {x}}$ weakly increases to its maximum, that is, it is not decreasing at any point before it reaches its maximum. Suppose not. Then by continuity of $v_{ \hat {x}}$ and its derivative, there exist $x_{1}, x_{2} \in[0, \hat {x}]$ such that

(77)

(78)

Then (45) and (77) imply that

Comparing this with (78), we have $\phi(x_{1}, v_{ \hat {x}}(x_{1})) > \phi(x_{2}, v_{ \hat {x}}(x_{1}))$, which contradicts Lemma 7. Therefore, $v_{ \hat {x}}$ must increase weakly to its maximum value on $[0, \hat {x}]$.

As the second step, we show that $v_{ \hat {x}}$ cannot be constant on any interval. Thus, we conclude that it must strictly increase to its maximum. To see this, suppose that $v_{ \hat {x}}$ is constant on some interval [x ₁,x ₂]. Then $v'_{ \hat {x}}(x) = 0$ for x∈[x ₁,x ₂], and therefore, it follows from (45) that $\phi(x, v_{ \hat {x}}(x)) = \phi ( \hat {x},p)$ for x∈[x ₁,x ₂]. However, since $\phi(x_{1}, v_{ \hat {x}}(x_{1})) = \phi( \hat {x}, p)>0$ and $v'_{ \hat {x}}(x_{1}) = 0$, one can argue from Lemma 7 that

(79)

But then we also have from (45) and $v'_{ \hat {x}}(x) = 0$ for x∈(x ₁,x ₂] that

which contradicts (79). Thus, $v_{ \hat {x}}$ cannot be constant on any interval, and we conclude that it strictly increases to its maximum on $[0, \hat {x}]$. □

Proof of Proposition 4

That ζ(⋅;p) is strictly increasing follows from part (ii) of Proposition 3 and (47). Also note from part (ii) of Lemma 5 and the fact that ϕ(x,v)=xψ(x,v)−ηv that $\phi( \underline {x}(p), p) = 0$. Combining this with the fact that ϕ(0,0)=0 gives $v_{ \underline {x}(p)} (\cdot; p) \equiv0$. Therefore, $\zeta( \underline {x}(p); p) = 0$.

To show that $\lim_{ \hat {x}\rightarrow\infty} \zeta( \hat {x}; p) = \infty$ for $p \in(0, \bar{p})$, note that

from which it follows that for x>0 sufficiently small (so that $v_{ \hat {x}}(s) \geq0$ for all s∈(0,x))

That is,

(80)

Moreover, as $\hat {x}\rightarrow\infty$, we have $\phi( \hat {x}, p) \rightarrow\infty$ because $\phi( \hat {x}, p) = \hat {x}\psi ( \hat {x}, p) - \eta p$ and $\lim_{ \hat {x}\rightarrow\infty} \psi( \hat {x}, p) > 0$ since $p< \bar {p}$. Therefore, the right-hand side of (80) tends to infinity, and hence, $\zeta( \hat {x}, p) \rightarrow \infty$.

To prove that ζ is continuous, we first prove that $v_{ \hat {x}}(x)$ is continuous in $\hat {x}$, uniformly over compact intervals [0,K], K>0. To this end, let $\hat {x}> \underline {x}(p)$ and $\{ \hat {x}_{n} \}$ be a sequence converging to $\hat {x}$ where $\hat {x}_{n} \geq \underline {x}(p)$. It suffices to show that $v_{ \hat {x}_{n}} (x) \rightarrow v_{ \hat {x}}(x)$ as n→∞ uniformly in x (over compact intervals). Recall that ψ(x,v) is Lipschitz continuous in v uniformly in x (see Lemma 1) and that ϕ(x,p)=xψ(x,v)−ηv. Therefore, ϕ(x,v) is Lipschitz continuous in v (uniformly in x when x∈[0,K], i.e. over compact intervals). Pick K sufficiently large so that $\hat {x}_{n} \leq K< \infty$ for all n. Then we write

where c _K is the uniform Lipschitz constant of ϕ(x,⋅) for x∈[0,K]. Then by Gronwall’s inequality, cf. p. 78 of Oksendal [44], it follows that

Therefore the sequence of functions $\{ v_{ \hat {x}_{n}} \}$ is a Cauchy sequence (uniformly in x∈[0,K]). Then for each x∈[0,K], we have

One can interchange the limit and the integral since $\phi(s, v_{ \hat {x}_{n}}(s))$ converges uniformly in s as n→∞, which follows from the uniform convergence of $v_{ \hat {x}_{n}}$ (on [0,K]) and the Lipschitz continuity of ϕ uniformly in s∈[0,K]. Then since ϕ(⋅,p) is also continuous, the following holds:

which shows that $\tilde{v}$ is continuously differentiable and solves the initial value problem IVP($\hat {x}$) on [0,K]. By the uniqueness of the solution to the initial value problem IVP($\hat {x}$) it follows that $\tilde{v} = v_{ \hat {x}}$. Therefore, $v_{ \hat {x}_{n}} \rightarrow v_{ \hat {x}}$ as n→∞ uniformly over compact intervals.

We now combine these results to prove that ζ(⋅;p) is continuous. To this end, fix $\hat {x}_{1} > \underline {x}(p)$ and let ϵ>0. Since $v_{ \hat {x}}(x)$ is continuous in $\hat {x}$ on compact intervals [0,K] for each K>0, there exists $\delta(K) \in(0, \underline {x}(p))$ such that $|v_{ \hat {x}_{1}}(x) - v_{ \hat {x}_{2}}(x)| < \epsilon/2$ for all x∈[0,K] whenever $| \hat {x}_{1} - \hat {x}_{2}| < \delta(K)$. Also for $K > \underline {x}(p)$, define

and observe that

Moreover, observe from (45)–(46) that for all $\hat {x}\in( \underline {x}(p), K]$ and $x_{1}, x_{2} \in[0, \hat {x}]$ that

(81)

Let K be sufficiently large, i.e. $K \geq2 \hat {x}_{1}$, and define

and consider $\hat {x}_{2}$ such that $| \hat {x}_{1} - \hat {x}_{2}| < \hat{\delta }(K)$. Consider the following two cases:

Case 1: $\hat {x}_{2} < \hat {x}_{1}$. Then $\zeta( \hat {x}_{2}) < \zeta( \hat {x}_{1})$. Choose $x_{1}^{*}$ such that $v_{ \hat {x}_{1}}(x^{*}_{1}) = \zeta( \hat {x}_{1})$. Then by (81) and definitions of $x_{1}^{*}$ and ζ it follows that

Then consider the following two subcases:

Case 1a: $x^{*}_{1} \leq \hat {x}_{2}$. Then $\zeta( \hat {x}_{2}) \geq v_{ \hat {x}_{2}}(x_{1}^{*}) \geq v_{ \hat {x}_{1}}(x_{1}^{*}) - \epsilon/2 = \zeta( \hat {x}_{1}) - \epsilon/2$.

Case 1b: $x^{*}_{1} > \hat {x}_{2}$. Then since $x_{1}^{*} \in( \hat {x}_{2}, \hat {x}_{1}]$, we have by (81) that

Therefore, in either case we have $\zeta( \hat {x}_{1}) \geq\zeta( \hat {x}_{2}) - \epsilon$, and combining this with $\zeta( \hat {x}_{2}) \leq\zeta( \hat {x}_{1})$ gives $|\zeta( \hat {x}_{2}) - \zeta( \hat {x}_{1})| < \epsilon$.

Case 2: $\hat {x}_{2} > \hat {x}_{1}$. Then $\zeta( \hat {x}_{1}) < \zeta( \hat {x}_{2})$. Choose $x_{2}^{*}$ such that $v_{ \hat {x}_{2}}(x^{*}_{2}) = \zeta( \hat {x}_{2})$. Then by (81) and definitions of $x_{1}^{*}$ and ζ, it follows that

Then consider the following two subcases:

Case 2a: $x^{*}_{2} \leq \hat {x}_{1}$. Then $\zeta( \hat {x}_{1}) \geq v_{ \hat {x}_{1}}(x_{2}^{*}) \geq v_{ \hat {x}_{2}}(x_{2}^{*}) - \epsilon/2 = \zeta( \hat {x}_{2}) - \epsilon/2$.

Case 2b: $x^{*}_{2} > \hat {x}_{1}$. Then since $x_{2}^{*} \in( \hat {x}_{1}, \hat {x}_{2}]$, we have

Therefore, in either case we have $\zeta( \hat {x}_{1}) \geq\zeta( \hat {x}_{2}) - \epsilon$, and combining this with $\zeta( \hat {x}_{1}) \leq\zeta( \hat {x}_{2})$ gives $|\zeta( \hat {x}_{2}) - \zeta( \hat {x}_{1})| < \epsilon$.

Combining cases 1 and 2, we conclude that ζ is continuous. □

Proof of Corollary 1

It is clear from Proposition 4 that there exists x(p) such that ζ(x(p);p)=p. Moreover, by Proposition 3, v _x(p)(⋅) increases strictly to its maximum value of p on the interval [0,x(p)]. Denote this maximum by x ^∗. We argue that x ^∗=x(p). Suppose not, i.e. x ^∗<x(p). Then

which is a contradiction by Lemma 6. Thus x ^∗=x(p). Moreover, it follows from (44) that v′(x(p))=2/σ ²[ϕ(x(p),p)−ϕ(x(p),v _x(p)(x(p))]=0. □

Proof of Proposition 5

Note that by construction v(⋅;p) solve the initial value problem IVP(x(p)) on [0,x(p)], and by Corollary 1, v(⋅;p) is continuously differentiable on [0,∞). Hence the result follows. □

Proof of Proposition 6

Part (i). Suppose not. Then there exist $0 < p_{1} < p_{2} < \bar{p}$ such that x(p ₂)≤x(p ₁). Then

where the first inequality follows from Lemma 3, part (ii) of Lemma 5 and that ϕ(x,v)=xψ(x,v)−ηv, the second inequality follows from part (vi) of Lemma 5, and the last inequality follows since ϕ(x,⋅) is strictly decreasing. Since ϕ(x(p ₂),p ₂)<ϕ(x(p ₁),p ₁), we can argue as in the proof of part (ii) of Proposition 3 that

(82)

Then by definition of v(⋅;p) it follows that

(83)

To be more specific, the first inequality follows from part (iii) of Proposition 3 and that x(p ₁)≥x(p ₂), and the second inequality follows from (82). But (83), i.e. p ₁>p ₂ is clearly a contradiction. Therefore x(p) is strictly increasing on $(0,\bar{p})$.

Part (ii). Let $0<p_{1}<p_{2}<\bar{p}$ and consider

(84)

(85)

Suppose β(p ₂)=ϕ(x ₂(p ₂),p ₂)≤ϕ(x(p ₁),p ₁)=β(p ₁). Then we can argue as in the proof of part (ii) of Proposition 3 that $v_{x(p_{2})}(x) \leq v_{x(p_{1})}(x)$ for all x>0. Then using (84)–(85) and the fact that ϕ(x,v) is strictly decreasing in v, we conclude that $v'_{x(p_{2})} (x) < v'_{x(p_{1})} (x)$ for all x>0. Note, however, that

which implies x(p ₂)≤x(p ₁) because $v_{x(p_{2})}(\cdot)$ increases strictly to its maximum (at x(p ₂)) and $v'_{x(p_{2})} (x(p_{2})) = 0$. But clearly x(p ₂)≤x(p ₁) contradicts part (i). Thus, β(p ₂)>β(p ₁).

Part (iii). Since β(p ₂)>β(p ₁) for 0<p ₁<p ₂<∞, this follows along the lines of the proof of part (ii) of Proposition 3. □

Proof of Proposition 7

Part (i). Note that β(p) is the long-run average cost in an auxiliary problem where the system manager can turn away arriving jobs, but incurs a rejection penalty of p for doing so per such job. (Given Proposition 5, it is straightforward to verify this along the lines of Theorem 1 of Rubino and Ata [54].) In this auxiliary system, consider the feasible policy which keeps all workload in buffer 1 and never turns away any jobs. Let $\hat { W}$ and $\hat{ Q}$ denote the (limiting) workload and queue-length process under this policy ($\hat{ Q}_{ k}= 0$ for k=2,…,K). Clearly we have

where

Also consider the reflected Brownian motion X(t) on [0,∞) with drift rate η<0 and infinitesimal variance σ ². Note that X(t) is stochastically larger than W(t). Thus, by monotonicity of h ₂(⋅)

but the right-hand side converges to (see [23]):

because X(∞) has an exponential distribution with mean σ ²/2m. This gives a uniform upper bound on β(p). Thus, β ^∗<∞.

Part (ii). Recall that $x(p) > \underline {x}(p)$ by construction, and that $\lim_{p\rightarrow \bar {p}} \underline {x}(p)= \infty$ by part (iv) of Lemma 5. Hence the result follows.

Part (iii). Recall that by construction 0≤v(x;p)≤p for all x≥0. Then letting $p\rightarrow \bar {p}$ gives

(86)

Since $\bar {p}< \infty$ by Lemma 4, this proves that v ^∗(x)<∞ for all x≥0. Also note that

(87)

Since v ^∗(⋅) is nondecreasing, which it inherits from v(⋅;p), and that x(p)↗∞ as $p \rightarrow \bar {p}$, we conclude from (86)–(87) that $\lim_{x\rightarrow\infty} v^{*}(x) = \bar {p}$. □