Wireless three-hop networks with stealing II: exact solutions through boundary value problems

Abstract

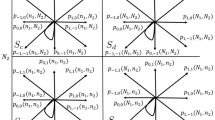
We study the stationary distribution of a random walk in the quarter plane arising in the study of three-hop wireless networks with stealing. Our motivation is to find exact tail asymptotics (beyond logarithmic estimates) for the marginal distributions, which requires an exact solution for the bivariate generating function describing the stationary distribution. This exact solution is determined via the theory of boundary value problems. Although this is a classical approach, the present random walk exhibits some salient features. In fact, to determine the exact tail asymptotics, the random walk presents several unprecedented challenges related to conformal mappings and analytic continuation. We address these challenges by formulating a boundary value problem different from the one usually seen in the literature.

Appendix A: Resultants

Generally speaking, when we have two polynomials in two variables, say,

$$\begin{aligned} f_1(x,y)&= a_0(y) + a_1(y) x +\cdots + a_n(y)x^n, \\ f_2(x,y)&= b_0(y) + b_1(y) x +\cdots + b_m(y)x^m, \end{aligned}$$

the resultant of the polynomials $f_1$ and $f_2$ with respect to $x$ is the determinant $\mathrm Res _x(f_1,f_2)$ of the matrix

$$\begin{aligned} \left( \begin{array}{cccccc} a_n&\cdots&a_0&0&\cdots&\cdots \\ 0&a_n&\cdots&a_0&0&\cdots \\ \cdots&\cdots&\cdots&\cdots&\cdots&\cdots \\ \cdots&\cdots&0&a_n&\cdots&a_0 \\ b_m&\cdots&b_0&0&\cdots&\cdots \\ 0&b_m&\cdots&b_0&0&\cdots \\ \cdots&\cdots&\cdots&\cdots&\cdots&\cdots \\ \cdots&\cdots&0&b_m&\cdots&b_0 \\ \end{array} \right) \begin{array}{c} \left\} \begin{array}{c}\\ m \text{ rows} \\ \\ \end{array} \right. \\ \\ \left\} \begin{array}{c}\\ n \text{ rows}\\ \\ \end{array} \right.\end{array} \end{aligned}$$

which is a polynomial in $y$. The polynomials $f_1$ and $f_2$ have a non-trivial root $(x_0,y_0)$ in common if and only if the resultant with respect to $x$ is 0 at $y_0$. This leads to the resolution of a polynomial equation. Note that by adding to the $(m+n)$th column, the $i$th column multiplied by $x^{m+n-i}$ for $0\le i<n+m$, $\mathrm Res _x(f_1,f_2)$ is equal to the determinant of the matrix

$$\begin{aligned} \left( \begin{array}{cccccc} a_n&\cdots&a_0&0&\cdots&x^{m-1}f_1\\ 0&a_n&\cdots&a_0&0&x^{m-2}f_1\\ \cdots&\cdots&\cdots&\cdots&\cdots&\cdots \\ \cdots&\cdots&0&a_n&\cdots&f_1\\ b_m&\cdots&b_0&0&\cdots&x^{n-1}f_2 \\ 0&b_m&\cdots&b_0&0&x^{n-2}f_2\\ \cdots&\cdots&\cdots&\cdots&\cdots&\cdots \\ \cdots&\cdots&0&b_m&\cdots&f_2 \\ \end{array} \right), \end{aligned}$$

which can written as $p(x,y)f_1(x,y) +q(x,y)f_2(x,y)$, where $p$ and $q$ are polynomials in variables $x$ and $y$.

1.1 A.1. Resultants of the polynomials $h_1$ and $h_2$

1.1.1 A.1.1. Resultant in $x$

The resultant in $x$ is the determinant of the matrix

$$\begin{aligned} \left( \begin{array}{cccc} -2(1-p) y&2(3y-1-p)&-2y^2&0\\ 0&-2(1-p) y&2(3y-1-p)&-2y^2 \\ (1+2p)y&-2(1+p)&y^2&0 \\ 0&(1+2p)y&-2(1+p)&y^2 \end{array} \right), \end{aligned}$$

Straightforward computations show that

$$\begin{aligned} \mathrm{Res}_{x}({h_1}, {h_2}; {y}) = 36y^3(y-1) \mathcal Q _x(h_1,h_2;y), \end{aligned}$$

where

$$\begin{aligned} \mathcal Q _x(h_1,h_2;y) = p^2 y^2+(1+p)^2 y -(1+p)^2. \end{aligned}$$

It is easily checked that the quadratic polynomial $\mathcal Q _x(h_1,h_2;y)$ has two roots with opposite sign, as stated in Sect. 3. The positive root is $y^*$ and the negative root is $y_*$ given by Eqs. (13) and (14), respectively. In addition, the value of the polynomial $\mathcal Q _x(h_1,h_2;y)$ at the point 1 is equal to $p^2$, which implies that $y^*<1$.

1.1.2 A.1.2. Resultant in $y$

The resultant in $y$ is the determinant of the matrix

$$\begin{aligned} \left( \begin{array}{cccc} -2&2(3-(1-p)x)x&-2(1+p)x&0 \\ 0&-2&2(3-(1-p)x)x&-2(1+p)x \\ 1&(1+2p)x^2&-2(1+p)x&0 \\ 0&1&(1+2p)x^2&-2(1+p)x \end{array} \right), \end{aligned}$$

and is equal to

$$\begin{aligned} \mathrm{Res}_{y}({h_1}, {h_2}; {x}) = 36(1+p)x^2(x-1)(px^2+(1-p)x-(1+p)). \end{aligned}$$

The quadratic polynomial in the right-hand side of the above equation has two real roots with opposite signs; the positive root is $x^*$ and the negative root if $x_*$ given by Eqs. (17) and (18), respectively.

As the value of this quadratic polynomial at the point 1 is equal to $-p$, $x^*>1$.

1.2 A.2. Resultants of the polynomials $h_1$ and $h_3$

1.2.1 A.2.1. Resultant in $y$

The resultant in $y$ of the polynomials $h_1(x,y)$ and $h_3(x,y)$ is equal to the determinant of the matrix

$$\begin{aligned} \left( \begin{array}{cccc} -2&2(3-(1-p)x)x&-2(1+p)x&0 \\ 0&-2&2(3-(1-p)x)x&-2(1+p)x \\ -2&(1-p)x^2&(1+p)x&0 \\ 0&-2&(1-p)x^2&(1+p)x \end{array} \right). \end{aligned}$$

Straightforward computations show that

$$\begin{aligned} \mathrm{Res}_{y}({h_1}, {h_3}; {x}) = 36x^2(1+p)(x-1)(1+p-(1-p)x). \end{aligned}$$

The roots of this polynomial are 0, 1 and $(1+p)/(1-p)$.

1.2.2 A.2.2. Resultant in $x$

The resultant in $x$ is the determinant of the matrix

$$\begin{aligned} \left( \begin{array}{cccc} -2(1-p) y&2(3y-1-p)&-2y^2&0\\ 0&-2(1-p) y&2(3y-1-p)&-2y^2 \\ (1-p)y&1+p&-2y^2&0 \\ 0&(1-p)y&1+p&-2y^2 \end{array} \right) \end{aligned}$$

and is equal to

$$\begin{aligned} \mathrm{Res}_{x}({h_1}, {h_3}; {y}) = 36y^4(1-p)(y-1)((1-p)y-1-p). \end{aligned}$$

The roots of this polynomial are 0, 1, and $(1+p)/(1-p)$.