Abstract
Event-driven programming has become a major paradigm in developing concurrent, distributed systems. Its benefits are often informally captured by the key tenet of “decoupling,” a notion which roughly captures the ability of processes to join and leave (or fail) applications dynamically, and to be developed by independent parties. Programming models for event-driven programming either make it hard to globally reason about control flow, thus hampering sound execution, or sacrifice decoupling to aid in reasoning about control flow. This work fills the gap by introducing a programming model—dubbed cooperative decoupled processes—that achieves both decoupling and global reasoning about control flow. We introduce this programming model through an event calculus, loosely inspired by the Join calculus, that enables reasoning about cooperative decoupled processes through the concepts of pre- and postconditions. A linear type system controls aliasing of events to avoid a break of control flow and thus safe exchange of shared events. Fundamental properties of the type system such as subject reduction, migration safety, and progress are established.







Similar content being viewed by others
Notes
The manual stack is modeled as in Adya et al. (2002).
For presentation reasons without affecting the correctness of the operational and static semantics, we write M 2 instead of writing l 1 & & l n . This style is similar to the reduction rule in the Join calculus of Fournet and Gonthier (1996).
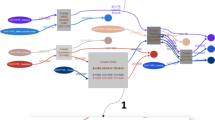
This is the only handler that can take place. The suppression handlers do not take place given the presence of
 and
and  in the site. The event describing a precondition guarding each handler is not present, prohibiting an arbitrary order of handler occurrences.
in the site. The event describing a precondition guarding each handler is not present, prohibiting an arbitrary order of handler occurrences.
References
Adya, A., Howell, J., Theimer, M., Bolosky, W.J., & Douceur, J.R. (2002). Cooperative task management without manual stack management. In USENIX (pp. 289–302).
Aldrich, J., Sunshine, J., Saini, D., & Sparks, Z. (2009). Typestate-oriented programming. In OOPSLA ’09 (pp. 1015–1022). ACM.
Association NFP (2015). Codes and standards. http://www.nfpa.org/.
Bejleri, A., Aldrich, J., & Bierhoff, K. (2006). Ego: controlling the power of simplicity. In FOOL/WOOD 06.
Bejleri, A., Mezini, M., & Eugster, P. (2016). Cooperative decoupled processes: the e-calculus and linearity. In MODULARITY.
Benton, N., Cardelli, L., & Fournet, C. (2004). Modern concurrency abstractions for c#. ACM Transactions on Programming Languages and Systems, 26(5), 769–804.
Berry, G., & Boudol, G. (1992). The chemical abstract machine. Theoretical Computer Science, 96(1), 217–248.
Bidinger, P., & Stefani, J.B. (2003). The kell calculus: operational semantics and type system. In FMOODS (pp. 109–123): Springer.
Bolosky, W.J., & et al (2000). Feasibility of a serverless distributed file system deployed on an existing set of desktop pcs. In SIGMETRICS ’00 (pp. 34–43).
Chin, B., & Millstein, T. (2006). Responders: language support for interactive applications. In ECOOP.
Courtenage, S. (2002). Specifying and detecting composite events in content-based publish/subscribe systems. In ICDCS Workshops (pp. 602–610).
Crafa, S., & Padovani, L. (2015). The chemical approach to typestate-oriented programming. In OOPSLA.
Cunningham, R., & Kohler, E. (2005). Making events less slippery with eel. In HOTOS.
Deniélou, P.M., & Yoshida, N. (2011). Dynamic multirole session types. In POPL ’11 (pp. 435–446).
Desai, A., Gupta, V., Jackson, E., Qadeer, S., Rajamani, S., & Zufferey, D. (2013). P: safe asynchronous event-driven programming. SIGPLAN Notices, 48(6).
Eugster, P.T., Felber, P.A., Guerraoui, R., & Kermarrec, A.M. (2003). The many faces of publish/subscribe. ACM Computing Surveys, 35(2), 114–131.
Fiege, L., Mezini, M., Mühl, G., & Buchmann, A.P. (2002). Engineering event-based systems with scopes. In ECOOP ’02 (pp. 309–333).
Floyd, S., & et al. (1997). A reliable multicast framework for light-weight sessions and application level framing. IEEE/ACM Transactions Network, 5(6).
Foltzer, A., Kulkarni, A., Swords, R., Sasidharan, S., Jiang, E., & Newton, R. (2012). A meta-scheduler for the par-monad: Composable scheduling for the heterogeneous cloud. SIGPLAN Notices, 47(9).
Fournet, C., & Gonthier, G. (1996). The reflexive cham and the join-calculus. In POPL (pp. 372–385).
Fournet, C., Gonthier, G., Lévy, J.J., Maranget, L., & Rémy, D. (1996). A calculus of mobile agents. In CONCUR (pp. 406–421).
Fournet, C., Laneve, C., & Maranget, L. (1997). Implicit typing ‘a la ml for the join-calculus. In Concur (pp. 196–212): Springer.
Franklin, M., & Zdonik, S. (1997). A framework for scalable dissemination-based systems. SIGPLAN Notices, 32(10).
Friedman, D.P., Haynes, C.T., & Kohlbecker, E.E. (1984). Programming with continuations. In PTPE (pp. 263–274).
Garcia, J., Popescu, D., Safi, G., Halfond, W., & Medvidovic, N. (2013). Identifying message flow in distributed event-based systems. In ESEC/FSE (pp. 367–377).
Gasiunas, V., Satabin, L., Mezini, M., Nez, A.N., & Noyé, J. (2011). EScala: modular event-driven object interactions in scala. In AOSD (pp. 227–240).
Gelernter, D. (1985). Generative communication in linda. ACM Transactions on Programming Languages and Systems, 7(1).
Germain, F., Lacoste, M., & Stefani, J.B. (2002). An abstract machine for a higher-order distributed process calculus. Electronic Notes in Theoretical Computer Science, 66(3), 145–169.
Girard, J.Y. (1987). Linear logic. Theoretical Computer Science, 50, 1–102.
Gustafsson, A. (2005). Threads without the pain. Queue, 3(9).
Haller, P., & Cutsem, T.V. (2008). Implementing joins using extensible pattern matching. In COORDINATION.
Haller, P., & Odersky, M. (2006). Event-based programming without inversion of control. In JMLC.
Haller, P., & Odersky, M. (2009). Scala actors: unifying thread-based and event-based programming. Theoretical Computer Science, 410(2–3).
Ham, J.M.V., Salvaneschi, G., Mezini, M., & Noyé, J. (2014). Jescala: modular coordination with declarative events and joins. In MODULARITY (pp. 205–216).
Hinze, A., & Voisard, A. (2002). A parameterized algebra for event notification services. In TIME (pp. 61–63).
Hu, R., Kouzapas, D., Pernet, O., Yoshida, N., & Honda, K. (2010). Type-safe eventful sessions in java. In ECOOP.
Kobayashi, N., Pierce, B.C., & Turner, D.N. (1999). Linearity and the pi-calculus. ACM Transactions on Programming Languages and Systems, 21(5), 914–947.
Lamport, L. (1978). Time, clocks, and the ordering of events in a distributed system. Communication of the ACM, 21(7), 558–565.
Li, P., & Zdancewic, S. (2007). Combining events and threads for scalable network services implementation and evaluation of monadic application-level concurrency primitives. In PLDI.
Ousterhout, J.K. (1996). Why threads are a bad idea (for most purposes), Usenix (Invited talk).
Parnas, D.L. (1972). On the criteria to be used in decomposing systems into modules. Communications of the ACM. In 15(12).
Pnueli, A. (1977). The temporal logic of programs, FOCS (pp. 46–57).
Sánchez, C., Sankaranarayanan, S., Sipma, H., Zhang, T., Dill, D.L., & Manna, Z. (2003). Event correlation: language and semantics. In EMSOFT (pp. 323–339).
Schmitt, A., & Stefani, J.B. (2003). The m-calculus: a higher-order distributed process calculus, POPL (pp. 50–61).
Shih, E., Bahl, P., & Sinclair, M.J. (2002). Wake on wireless: an event driven energy saving strategy for battery operated devices. In MobiCom ’02 (pp. 160–171).
Strom, R.E., & Yemini, S. (1986). Typestate: a programming language concept for enhancing software reliability. IEEE Transactions on Software Engineering, 12(1), 157–171.
Sunshine, J., Naden, K., Stork, S., Aldrich, J., & Tanter, É. (2011). First-class state change in plaid. In OOPSLA (pp. 713–732).
von Behren, J.R., Condit, J., & Brewer, E.A. (2003). Why events are a bad idea (for high-concurrency servers). In HotOS (pp. 19–24).
Welsh, M., Culler, D.E., & Brewer, E.A. (2001). Seda: An architecture for well-conditioned, scalable internet services. In SOSP (pp. 230–243).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Combination of types and typing rules for the runtime
Combination of types for the runtime include combination of postcondition and product events created during evaluation:

to capture exchange of events at runtime. The typing rule for the runtime include typing of init and reactants:
to preserve the static type with the runtime type, after stated (declared) events are consumed. These rules allow statement and proof of subject reduction. Combination with other products for the name in the \(\vdash _{r}\) judgment will combine to the same type rp.
Appendix B: Properties
This section gives the full proof of subject congruence and reduction, migration safety, progress along lemmas used in their proofs. We describe the approach taken for proving type safety for our system. We define important conditions and present the key lemmas needed for proving subject reduction (preservation) and migration safety. We consider all cases for both subject reduction and migration safety. For subject reduction, we use the following lemmas and propositions. Given typeable terms, the first lemma describes structure properties of type environments where I, J, K, M, N denote sets of naturals.
Lemma 1 (Type environment inversion)
-
(1)
If \({\Gamma } \vdash {M}\) then \({\Gamma } = \{{l}_{i}:\alpha _{i}^{i \in I}\}\) where \(\alpha _{i} = \{{l}_{p}@A_{i}, p@ \tilde {A}_{i}\}\).
-
(2)
If \({\Gamma } \vdash _{r} {M}\) then Γ = {l i : r i∈I}@A.
-
(3)
If \({\Gamma } \vdash _{p} {M}\) then Γ = {l i : p i∈I}@A.
-
(4)
If \({\Gamma } \vdash _{D} {D}\) then \({\Gamma } = \{{l}_{i} : \alpha _{i}^{i \in I} \} \cup \{{l}_{i} : \beta _{i}^{i \in J}\} \cup \{{l}_{i} : {l}_{p}@A_{i}^{i \in K}\} \cup \{{l}_{i} : p@\tilde {A}_{i}^{i \in L}\}\) where \(\alpha _{i} \in \{{l}_{r}@\tilde {A}_{i}, {l}_{r}{l}_{p}@\tilde {A}_{i}\}\) and \(\beta _{i} = \{r@\tilde {A}_{i}, rp@A_{i}\}\) .
-
(5)
If \({\Gamma } \vdash {\textup {\textsf {def}}\ {D} \ \textup {\textsf {in}}\ {M}}\) then \({\Gamma } = \{{l}_{i} : \alpha _{i}^{i \in I} \} \cup \{{l}_{i} : \beta _{i}^{i \in J}\} \cup \{{l}_{i} : {l}_{p}@A_{i}^{i \in K}\} \cup \{{l}_{i} : p@\tilde {A}_{i}^{i \in L}\}\) where \(\alpha _{i} \in \{{l}_{r}@\tilde {A}_{i}, {l}_{r}{l}_{p}@\tilde {A}_{i}\}\) and \(\beta _{i} = \{r@\tilde {A}_{i}, rp@A_{i}\}\) .
Proof
The proof is tedious but straightforward by typing and combination rules. □
We note \(\mathsf {dom_{ln}}({\Gamma }) = \{{l}_{i}^{i \in I}\}\) if \({l}:{l}_{r}@ \tilde {A}, {l}:{l}_{p}@A, {l}:{l}_{r}{l}_{p}@\tilde {A} \in {\Gamma }\) as the set of names denoting linear types: preconditions and postconditions.
Proposition 3 (Associativity of ⊎)
Given \({\Gamma }_{1} = \{{l}_{i} : \alpha _{i}^{i \in I} \} \cup \{{l}_{i} : \beta _{i}^{i \in J}\} \cup \{{l}_{i} : {l}_{p}@A_{i}^{i \in K}\} \cup \{{l}_{i} : p@\tilde {A}_{i}^{i \in L}\}\) , \({\Gamma }_{2} = \{{l}_{i}:p@\tilde {A}_{i}^{i \in N}\} \cup \{{l}_{i}:{l}_{p}@A_{i}^{i \in N^{\prime }}\}\) , \({\Gamma }_{3} = \{{l}_{i}:p@\tilde {A}_{i}^{i \in M}\} \cup \{{l}_{i}:{l}_{p}@A_{i}^{i \in M^{\prime }}\}\) where \(\alpha _{i} \in \{{l}_{r}@\tilde {A}_{i}, {l}_{r}{l}_{p}@\tilde {A}_{i}\}\) and \(\beta _{i} = \{r@\tilde {A}_{i}, rp@A_{i}\}\) is defined if and only if Γ1 ⊎ S (Γ2 ⊎Γ3)is defined, (Γ1 ⊎ S Γ2) ⊎Γ3 = Γ1 ⊎ S (Γ2 ⊎Γ3)and \(\mathsf {dom_{ln}}({\Gamma }_{1}) \cap \mathsf {dom_{ln}}({\Gamma }_{2}) \cap \mathsf {dom_{ln}}({\Gamma }_{3}) = \emptyset \) .
Proof
Case analysis on the membership of type assertions in Γ1,Γ2and Γ3. We give the proofof “if (Γ1 ⊎ S Γ2) ⊎Γ3is definedthen Γ1 ⊎ S (Γ2 ⊎Γ3)is defined”.The proof of “if Γ1 ⊎ S (Γ2 ⊎Γ3)is defined then (Γ1 ⊎ S Γ2) ⊎Γ3is defined” is symmetric.
- Case l :
-
∈ d o m(Γ1), d o m(Γ2), d o m(Γ3).We have that \({\Gamma }_{1}({l}) \in \{{l}_{r}@\tilde {A}, {l}_{r}{l}_{p}@\tilde {A}, {l}_{p}@A, r@\tilde {A}\),\(rp@A, p@\tilde {A}\}, {\Gamma }_{2}({l}) \in \{{l}_{p}@B, p@\tilde {B}\}\),\({\Gamma }_{3}({l}) \in \{{l}_{p}@C, p@\tilde {C}\}\).\(\{{l}_{r}@\tilde {A}, {l}_{r}{l}_{p}@\tilde {A}, {l}_{p}@A\),\( r@\tilde {A}, rp@A, p@\tilde {A}\} \uplus _{S} \{{l}_{p}@B\),\(p@\tilde {B}\}\)is defined by assumption and the result is \(\{{l}_{r}{l}_{p}@\{\tilde {A}, B\}\),\( {l}_{p}@A, rp@\{A, B\}, p@\{\tilde {A}, B\}\}\)by definition of combination rules. Next, we have that\(\{{l}_{r}{l}_{p}@\{\tilde {A}, B\}, {l}_{p}@A, rp@\{A, B\}\),\( p@\{\tilde {A}, \tilde {B}\}\} \uplus \{{l}_{p}@C, p@\tilde {C}\}\)is defined only for the nonlinear names \(\{rp@A, p@\{\tilde {A}, \tilde {B}, \tilde {C}\}\}\).Two linear types and, one linear and one nonlinear do notcombine by definition. On the other side, we have that (Γ1 ⊎ S (Γ2⊎Γ3))(l) =Γ1(l)⊎ S (Γ2⊎Γ3)(l) =Γ1(l)⊎ S (Γ2(l)⊎Γ3(l)).In here, \(\{{l}_{p}@B, p@\tilde {B}\} \uplus \{{l}_{p}@C, p@\tilde {C}\}\)is defined only for nonlinear events by hypothesis, resulting in\(\{p@\{\tilde {B}, \tilde {C}\}\}\).\(\{{l}_{r}@\tilde {A}, {l}_{r}{l}_{p}@\tilde {A}, {l}_{p}@A\),\(r@\tilde {A}, rp@A, p@\tilde {A}\} \uplus _{S} \{p@\{\tilde {B}, \tilde {C}\}\}\)is defined only for nonlinear events, resulting in {r p@A,\(p@\{\tilde {A}, \tilde {B}, \tilde {C}\}\}\).
- Case l :
-
∈ d o m(Γ1), d o m(Γ2), l∉d o m(Γ3).So, ((Γ1 ⊎ S Γ2)⊎Γ3)(l) = (Γ1 ⊎ S Γ2)(l) =Γ1(l)⊎ S Γ2(l)is defined by assumption. On the other side, we have that (Γ1 ⊎ S (Γ2 ⊎Γ3)) (l) =Γ1(l) ⊎ S (Γ2 ⊎Γ3)(l) =Γ1(l) ⊎ S Γ2(l)is defined by hypothesis.
- Cases l :
-
∈ d o m(Γ1), d o m(Γ3), l∉d o m(Γ2)and l ∈ d o m(Γ2), d o m(Γ3), l∉d o m(Γ1)are similar to the one above.
- Cases l :
-
∈ d o m(Γ1), l∉d o m(Γ2), d o m(Γ3)and l ∈ d o m(Γ2), l∉d o m(Γ1), d o m(Γ3)and l ∈ d o m(Γ3), l∉d o m(Γ2), d o m(Γ1) are trivial.
□
Lemma 2 (Subject congruence)
If P ≡ Q then \({\Gamma } \vdash {P}\) iff \({\Gamma } \vdash {Q}\) .
Proof
By induction on the proof of P ≡ Q.We present only the case for rule ⌊STR-DEF⌋.Other cases are trivial. □
Case(Rule STR-DEF)
Proposition 4
If \((\{{l}_{i}:{l}_{p}\}^{i \in I}@A, {\Gamma }) \uplus _{S} {\Gamma }^{\prime }\) is defined and \(\{l_{i}\}^{i \in I}\) ⊄ \(dom({\Gamma }^{\prime })\) where \({\Gamma } = \{{l}_{i}:p@\tilde {A}_{i}\}^{i \in J}, {\Gamma }^{\prime }=\{{l}^{\prime }_{i}:\alpha _{i}\}^{i \in K}\) and \(\alpha \in \{{l}_{p}@A, p@\tilde {A}_{i}\}\) then \(({l}:\{{l}_{i}:{l}_{p}\}^{i \in I}@A, \{{l}_{i}:p@\tilde {A}_{i}\}^{i \in J}) \uplus \{{l}^{\prime }_{i}:\alpha _{i}\}^{i \in K}\) is defined.
Proof
Straightforward. By\(p@\tilde {A}_{i} \uplus p@\tilde {A}_{j} = p@\tilde {A}_{i}, \tilde {A}_{j}\)and combination rules. □
Proposition 5
If \((({\Gamma }, \{{l}_{i}:{l}_{r}@\tilde {A}_{i}\}^{i \in I}) \uplus _{H} ({\Gamma }^{\prime }, \{k:{l}_{p}@A_{i}\}^{i \in J})) \uplus _{S} ({\Gamma }_{1} \uplus {\Gamma }_{1}^{\prime })\) is defined, and {k}i∈J ⊄\(dom{({\Gamma }_{1}^{\prime })}\) then \((({\Gamma }, \{{l}_{i}:{l}_{r}@\tilde {A}_{i}\}^{i \in I}) \uplus _{H} ({\Gamma }^{\prime }, \{k:{l}_{p}@A_{i}\}^{i \in J})) \uplus _{S} (\{k:{l}_{p}@A_{i}\}^{i \in J},{\Gamma }^{\prime } \uplus {\Gamma }_{1}^{\prime })\) is defined.
Proof
By assumption {k}i∈J ⊄ \(dom{({\Gamma }_{1}^{\prime })}\)then \(\{{k}:{l}_{p}@A_{i}\}^{i \in J} \uplus {\Gamma }_{1}^{\prime }\)is defined. We must show that assumptions of linear types in\({\Gamma }_{1}^{\prime }\)are not on names appearing as well on assumptions of nonlinear\({\Gamma }^{\prime }\). By Prop. 3, we have that \((({\Gamma }, \{{l}_{i}:{l}_{r}@\tilde {A}_{i}\}^{i \in I}) \uplus _{H} ({\Gamma }^{\prime }, \{{k}:{l}_{p}@A_{i}\}^{i \in J})) \uplus _{S} ({\Gamma }_{1} \uplus {\Gamma }_{1}^{\prime }) = (({\Gamma }, \{{l}_{i}:{l}_{r}@\tilde {A}_{i}\}^{i \in I}) \uplus _{H} ({\Gamma }^{\prime }, \{{k}:{l}_{p}@A_{i}\}^{i \in J})\uplus {\Gamma }_{1}^{\prime }) \uplus _{S} {\Gamma }_{1}\).This implies that \(({\Gamma }^{\prime }, \{{k}:{l}_{p}@A_{i}\}^{i \in J})\uplus {\Gamma }_{1}^{\prime }\)is defined. By Prop 4, we conclude that \(({\Gamma }^{\prime }, \{{k}:{l}_{p}@A_{i}\}^{i \in J})\uplus {\Gamma }_{1}^{\prime }\)is defined. From here, one can easily conclude that\((({\Gamma }, \{{l}_{i}:{l}_{r}@\tilde {A}_{i}\}^{i \in I}) \uplus _{H} ({\Gamma }^{\prime }, \{{k}:{l}_{p}@A_{i}\}^{i \in J})) \uplus _{S} (\{{k}:{l}_{p}@A_{i}\}^{i \in J},{\Gamma }^{\prime } \uplus {\Gamma }_{1}^{\prime })\) is defined. □
Proposition 6
If (Γ1 ⊎ D Γ2) ⊎ S Γ3 is defined then Γ1 ⊎ S Γ3 is defined.
Proof
Straightforward since Γ1 ⊎ D Γ2(l) ∈ {l r , l r l p , r, r p, l p , p}and Γ1(l) ∈ {l r , l r l p , r, r p, l p , p}. □
Theorem 4 (Subject reduction)
If \({\Gamma } \vdash {P}\) and P → Q then \({\Gamma } \vdash {Q}\) .
Proof
We use induction on the derivation of P → Q. □
Case(R-Occ)
Note that \((({\Gamma }_{3} \uplus _{rea} {\Gamma }_{4}) \uplus _{H} ({\Gamma }_{4} \uplus _{pro} {\Gamma }_{5})) \uplus _{S} ({\Gamma }_{2}^{\prime } \uplus {\Gamma }_{2}^{\prime \prime }) = (({\Gamma }_{3} \uplus _{rea} {\Gamma }_{4}) \uplus _{H} ({\Gamma }_{4} \uplus _{pro} {\Gamma }_{5})) \uplus _{S} ({\Gamma }_{5} \uplus {\Gamma }_{6} \uplus {\Gamma }_{2}^{\prime \prime })\).
Case(Rule R-AddPre)
One can easily observe that \({\Gamma } = {\Gamma }^{\prime }\).
Case(Rule R-DisO)
One can easily observe that by having Γ2 ⊎ S Γ3 =Γ7 ⊎ S Γ3, once can conclude that by extending Γ3 with other handlers Γ4 that are compatible by assumption then Γ2 ⊎ S (Γ3 ⊎ D Γ4) =Γ7 ⊎ S (Γ3 ⊎ D Γ4).
Case(Rule R-Par)
Case(Rule R-Struct)
Theorem 5 (Subject reduction for programs)
If \(\emptyset {\vdash _{flows}} {P} \) and P → Q then \(\emptyset {\vdash _{flows}} {Q}\)
Proof
Follows as a corollary from Subject reduction Theorem 4. □
Theorem 6 (Migration safety)
Suppose \({\Gamma } \vdash {P}\) then for adding l to \({\mathcal {E}}\) where P \(\equiv {\mathcal {E}}[{l}]\) such that either \(\mathcal {E}\) contains:
-
1.
exactly one \({\mathcal {E}}_{pre}\langle {l} \rangle \) and l = i n i t
-
2.
exactly one pair of \(\mathcal {E}_{post}\langle {l} \rangle \) and \(\mathcal {E}_{pre}\langle {l} \rangle \)
-
3.
exactly one \(\mathcal {E}_{post}\langle {l} \rangle \) and many \(\mathcal {E}_{pre}\langle {l} \rangle \) in only one site
-
4.
many \(\mathcal {E}_{r}\langle {l} \rangle \) of the same flow
-
5.
many \(\mathcal {E}_{r}\langle {l} \rangle \) and many \(\mathcal {E}_{p}\langle {l} \rangle \) of the same flow
-
6.
exactly one \(\mathcal {E}_{r}\langle {l} \rangle \) and many \(\mathcal {E}_{p}\langle {l} \rangle \) of different flows
Proof
Let P ≡ l & P 0 & Q where P 0does not containglobal events and Q contains global events. By rule induction, we prove that P 0 has aname l as a reactant at a reaction of a site or a precondition or a pair of a precondition and postcondition orpairs of a reactant and products.
- Case:
-
(⌊T-GName⌋, ⌊T-RGName⌋, ⌊T-Site⌋, ⌊T-Handler⌋, ⌊T-Dis⌋, ⌊T-GPar⌋, ⌊T-PPar⌋, ⌊T-RPar⌋):Vacuous since the terms do not reduce at l.
- Case:
-
(⌊T-Par⌋): Suppose \({\Gamma } \vdash {P}\) and \({\Gamma }^{\prime } \vdash {Q}\)suchthat \({\Gamma } \uplus {\Gamma }^{\prime }\)is defined. By induction hypothesis, we can assume that P and Q satisfy the required condition.
-
1.
If only one party reduces at l then we conclude.
-
2.
If both processes reduce at l,hence Γand \({\Gamma }^{\prime }\),respectively, have a precondition or reactant at l and P and Q are not of the same flow. Then, \({\Gamma } \uplus {\Gamma }^{\prime }\)cannot not be defined by combination rules of ⊎.
-
1.
□
Theorem 7 (Progress)
If \(\emptyset \vdash _{flows} {P}\) and P is simple then P \(\longrightarrow {P}^{\prime }\) or inactive.
Proof
By induction on the derivation of the typing judgment.
Case
By induction on the derivation of the typing judgment, analyzing all possible cases, we prove thatgiven \({\Gamma } \vdash {P}\) and \({\Gamma } = \{{l}_{i}:{{l}_{r}{l}_{p}}/rp/{l}_{p}/p @{\Delta }_{i}\}^{i \in I}\) and P is simple then \(P \longrightarrow {P}^{\prime }\)or inactive.
Cases ⌊T-Dis⌋, ⌊T-Hand⌋, ⌊TInact⌋, ⌊T-PrePar⌋, ⌊T-RPar⌋, ⌊T-PostPar⌋, ⌊T-PPar⌋, ⌊T-PreName⌋, ⌊T-RName⌋, ⌊T-PostName⌋ and ⌊T-PName⌋ are vacuous.
Case
Case
Case
Similarly for rule ⌊T-GName⌋.
□
Rights and permissions
About this article
Cite this article
Bejleri, A., Mezini, M., Eugster, P. et al. Cooperative decoupled processes. Software Qual J 26, 1147–1183 (2018). https://doi.org/10.1007/s11219-017-9366-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11219-017-9366-6




 and
and  in the site. The event describing a precondition guarding each handler is not present, prohibiting an arbitrary order of handler occurrences.
in the site. The event describing a precondition guarding each handler is not present, prohibiting an arbitrary order of handler occurrences.