1 Introduction

Graph based researches have recently been captured wide attention by the information retrieval community, data processing and bio-informatics societies, artificial intelligence displine, operations research group, and more. Since the graphs are not only the general format of the indipendent item searches, but also much more advantageous for them to support the theoretical breakthrough. At first, once the query and the relevant results can be represented by a graph, which can provide the opportunities to apply huge theoretical resources mainly inherited from the previous mathematical achievements of the graph theory. For example, a web page or a social media can be represented by a node and the hyperlink between them by an edge, which will be exactly matched by a graph or digraph. In that case, it can be applied by a lot of graph theories developed so far such as centralities, degrees and diameters, trees and graph theorems, connectivity and diversity, cycle and cut, matrix calculations, network flow dynamics, sensitivity and duality, etc [1, 5, 22, 36,37,38].

Secondly, if the query results are represented by a linked result or a structured one, they can be more inclusive for the semantic representation and broadening in target applications [8, 36]. It can trigger much more enhanced user interface devices than the conventional document listing interfaces [2]. Thus the representation may be enhanced from the simple enumeration of texts to the higher level of graphic user interfaces such as Virtual Reality, eXtreme Reality, or Mixed Reality, so that much more different targets can be included such as bio-molecular structures, medical organisms, chemical reactions, architectural and topological applications, chronological relationships, micro and macro targets, etc [3, 11, 31]. Additionally for the mobile device applications with the limited screen size and personalization, they may be supported to optimize the content and to endow privacy consideration for mobile users [4, 28].

Another reason why the graph based approach is inevitable is that the size of bigdata increases exponentially. In the explosive growth of the big data will also increase the connectivity among them, so that the graph approach can be advantageous for the data processing, storing and retrieving information effectively. For example, there attacks the pagerank scores by increasing huge number of fake nodes and edges, which also can be analyzed and protected by the Search Engine Optimization approaches [14, 20]. This phenomenon emphasizes the importance of graph search methodologies reflecting complex structures and big data [8, 34]. Additionally, the heterogeneous network makes the problem the more difficult, since it includes not only the different types of objects that is not a homogeneous link between the nodes, but also a combination of different types of data intermixed with different data sources. Note that the conventional approaches have only considered the query and a single suitable result so far [2, 37].

Fig. 1
figure 1

Example of a heterogeneous connected graph: where PHR is a personal health record, Pubmed a medical publication database, and Geometric a location managing tool

Full size image

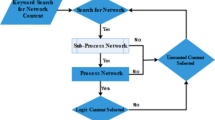
The way to solve this problem is called top-k graph search that is different from the top-k query processing, which provides a single item list as search results. The purpose of top-k graph search is not only a single node as a search result, but also nodes and hyper-graphs. Let’s take a closer look at the benefits of a top-k graph search with the Fig. 1. Suppose we want to retrieve the following information: ‘Find the right painkiller pharmacy with my medical record.’ There are many types of painkillers, where searching for the most popular ones from the web or Pubmed, they, however, also have revealed various side effects. For example, acetaminophen, known as tylenol, can strain the liver, and ibuprofen strains the kidneys, etc. In Aspirin, there have been reported the Prin allergia [5]. A PHR (personal health record) is a database through which patients’ health information and that of others for whom they are authorized in a private, secure, and confidential environment [11]. PHR database as an example is represented in Fig. 1, where we can append more accurate and personalized results and the availability of the selected painkiller can be checked by Geometric information.

The problem we want to solve in this study is “How can an efficient graph search be performed for the distributed heterogeneous sources?” One way to do the search with all the nodes and edges on which all the combinations of the nodes and edges need to be enumerated. Once the target data will be listed and sorted, a fair alternative may be drived by threshold algorithm (TA) [13, 40] that can be applied to the top-k query processing. TA would be one of the most frequently used algorithms that can find the optimal top-k solution without reading the remaining data less than the threshold obtained from a monotonic function. In the graph situation, however, the problem is that the number of candidate combinations per se becomes enormous before sorting and random accessing the target data, which makes the problem difficult. For example, if two pairs of node candidates are generated, then \({n\atopwithdelims ()2}\) needs to be listed which results the complexity to extend into combinations, where the combination will not be limited to two pairs, but needs enumerations for all the possible combinations such as \({n\atopwithdelims ()3}, {n\atopwithdelims ()4}, \ldots , {n\atopwithdelims ()n}\). After listing the target data combinations, upon which the sorting procedure will be followed, and then TA will work on it. Consequently, the advantage of TA rapidly disappears.

Thus, the problem we are dealing with is that of enumerating the graph top-k answer set, which contains all the results of a subgraph and a single entity as a result of a large and complex graph. In fact, since this problem is proved as NP-hard [19, 24], we propose a method to find the graph top-k answer more efficiently by using the new data structure while deriving the results with a lot of partial data acknowledging the threshold. In this paper, we propose a novel algorithm name as graph threshold algorithms (GTA) that generalizes TA to find the “connected result,” i.e., a subgraph, which takes into account the relevance of the objects with a query and the relationships among the objects simultaneously.

The main contributions of this work are as follows:

  1. 1.

    We propose a novel algorithm for the hyper node problem that incoporates the node as well as the graph as a whole top-k graph search target.

  2. 2.

    We exclude the unnecessary operations by theoretically deriving the size of the graph based on the graph threshold.

  3. 3.

    We prove GTA to be superior to the existing research methods experimentally on the real-world data.

The rest of the paper is organized as follows. Related works are presented in Sect. 2. How to apply the Threshold Algorithm to the graph environment and preliminaries are explained in Sect. 3. Out novel algorithms, NaïveGTA and GTA for top-k query processing is presented in Sects. 4 and 5 respectively. The experimental results are illustrated in Sects. 6 and 7 concludes the paper.

2 Related works

The related researches are classified into three directions according to the search method and the results. The first is the traditional top-k query processing methods that efficiently find k individual objects due to the set of query terms, which would have been and will be continued with respect to newly appearing various data types. The second is the keyword based graph search methods. For example, given the query keywords as \(Q_{set}\), \(\{\)“painkiller”, “PHR”, “Pubmed”\(\}\), then the result of top-k query processing will be a set of single nodes containing all the query keywords. The top-k query processing method has been working for finding a single list, but it does not provide the structural information (graph results) [8]. Another limitation has been reported that if the number of keywords increases, the result will inevitably be sacrificed by either the scarcity or duplication [34].

The third is that the top-k graph search where it can be sub-classified into the query type, search result type and data type. In [1, 6, 10, 16, 35, 43, 44], they converted the keywords to a graph query and searched for the subgraph with the isomorphic query graph. Many subgraph matching algorithms can be applied to graph-structured data regardless of unstructured (ex. Web, Doc) or semi-structured (ex. XML, RDF) or structured (ex. RDBMS). However, the limitation of these methods would be the burden to know the structure of the source and to construct an accurate query [17]. The success of these search stems from what it does not require, a specialized query language or knowledge of the underlying structure of the data [2]. In reality, it is difficult for users to create structured query terms with the unknown schema or the graph topology [16, 21].

Researches traditionally have taken only the keyword set as a query and expect to obtain both the graph results or single results. In [15, 23, 30], it depends on the fact that whether or not it will use a single objective function that optimizes only the edge weight of the graph result among the keyword nodes, or a bi-objective function that maximizes the relevance of the keyword node weights as well as the edge weights of the graph. In [15, 18, 33], these methods have an advantage that it can be applied to the structured target, ignoring the relevance with the query keyword and the keyword nodes. Conversely, the third methods are limited to semi-structured or unstructured data only [7, 20, 21, 27, 37]. Our approach in this regard, given the query set, is to calculate the top-k graph result effectively regardless of the characteristics of the domains.

However, there are limitations in applying the existing graph retrieval methods. (1) Many graph search methods require a fixed query graph as the query. The methods are called graph isomorphism problems [6, 8]. These are not suited to our problem to derive various search results that are not fixed size as a result set. (2) Other ways are to use the set of query terms as input and find k results with the least cost using the topological information of the graph which have been used to find the diameter of the graph, Minimum Spanning Tree or sum of distances among the result [15, 30, 33, 43]. This is not a complete solution because it does not take into account the node or object’s relevance. (3) Finally, there are methods to consider the node’s relevance and topological costs simultaneously, but they have a limitation that it works only in a structured environment like RDBMS or XML [18, 33, 34, 37].

It becomes crucial to efficiently process top-k queries in many interactive environments that contain huge amounts of data [8, 19, 37]. The efficient top-k processing, particularly in the domains such as the hidden Web, multimedia, and distributed transaction processing systems, has given significant impacts on performance. Given a monotonic aggregation function and a sorted list for each attribute, top-k search over the relevant data is to find the best results for the scoring function efficiently. FA [12] reads the values of each attribute and constructs sorted lists, where it is finalized with high probability for some monotonic scoring functions. The TA [13] improved FA in that it is optimal for all monotonic scoring functions, and allows early termination. In a nutshell, it reads the sorted lists and accesses by predicting the maximum possible score for the unseen data until top-k results are identified that has been exploited many different domains, but the variations of them mostly born in non-graph environments [26, 32, 41].

The objective of graph-based approaches is to minimize the weight of result graphs or trees. It has been tackled by formulating the Group Steiner Tree problem or Steiner Graph problem, which is known to be NP-complete [23, 25]. DPBF [9] is a dynamic programming algorithm to find the optimal Group Steiner Tree but remains exponential in the number of search terms results. STAR [23] is a pseudo-polynomial time algorithm for the Steiner Tree problem. It computes an initial solution fast and then improves this result iteratively. Most of the work in keyword search over graphs finds the connected minimal trees that has been tried to cover all the query keywords [16, 17]. However, it has been shown that finding subgraphs rather than trees can be much more useful and informative for the user query semantics [30, 36, 39].

It is significant for the next generation search whether or not the result can be a sub-graph of related information connected with semantic link or data-link. It is not easy to retrieve the best result from the weighted information connected with complex structures (e.g., Web, XML, relational database, Genomics, Data graph, Bio-informatics, etc.). Regarding this, information unit [29] inspired a Steiner graph search by devising an efficient index for the structural information as a unit where it can provide a top-k search result. After that, many of the Steiner graph based approaches [1, 21, 30, 43] have tried to find r-radius Steiner graphs that contain the maximum number of the input keywords. These approaches admit that it might miss some of the highly ranked r-radius Steiner graphs since the algorithm for finding r-radius graph disregards the input keywords. Also, it might produce duplicate and redundant results because they are sub-optimal [2].

Our motivation is to consider the graph topology as well as TA approach together. Since TA is exellent on the sorted results, but the number of node combinations from the graph and devising the hyper-graph topology is a challenging issue. We suggest a hyper-graph notion and the relevant ranking measure which can open a new opportunity to incorporate the information retrieval perspective in addition to data science point of views. One more thing to mention here is that the size of the input nodes will be increased exponentially on the graphs in general that coerces our problem from applying a deep learning network [42], which will be our future work.

3 Problem definition

We introduce the notations for Graph Threshold Algorithm (GTA). Let G(V, E) be an undirected graph with a set of node \(V=\{v_1,\ldots ,v_n\}\) and a set of edges \(E=\{(v_i,v_j)|v_i,v_j\in V \text { for } i,j=1,\ldots ,n\text { and }i\ne j\}\). Since the domain of GTA includes not only single nodes in V but also connected subgraphs of G(V, E), we define a hop node, that is vertices of a connected subgraph. Note that we only consider a connected subgraph of a given undirected graph.

Definition 1

(Hop node) Let H be a connected subgraph of undirected graph G(V, E). The set of all vertices of the subgraph H of G, h is the hop node of H.

Two different subgraphs may have the same hop node if they have the same node set. Hop nodes are devised for GTA results where h of H is on the weighted node information, not the topology of a subgraph as long as it is connected. We extend this hop node h notation to a single node \(v \in V\) since we can consider a single node itself is a subset of the connected subgraph. It means that we treat a node v in V is a singleton subset of V, \(\{v\}\subset V\), which is different as \(v\in V\) as conventional notation for a node. Hence, it is clear that the results for GTA is a subset of the power set \({\mathscr {P}}(V)\), whose nodes are hop nodes of V including all singleton subsets.

Definition 2

(Size of h and hop number) Let h be a hop node of V. Then the number of nodes in h is called the size of h denoted by |h|. In addition, \(|h|-1\) is called the hop number of h.

Let h be a hop node with size |h| induced from a subgraph H. Then the number of edges in H is at least \(|h|-1\) since it is connected. Hence, the hop number is the minimum number of edges needed to connect all nodes in a hop node h. Note that hop number is 0 for a singleton node.

Suppose that we consider m-dimensional query keywords [7]. We already have attribute scores for each node v in V. Hence, a hop node \(h=\{v\}\) with size 1 can be identified by a m-dimensional vector, denoted by s(h), which is induced from the attribute scores of original node n in V. For the sake of simplicity, we use \(s(h)=s(v)\) for a singleton hop node \(h=\{v\}\). However, we need to assign an m-dimensional vector for its attribute scores to a non-singleton hop node, which we define the average of attribute scores of all nodes in h [24].

Definition 3

(Attribute score for a hop node) Given a query \(Q(k_1,\ldots ,k_m)\), the attribute score of a hop node \(h=\{v_1,\ldots ,v_n\}\), denoted by s(h), is the average value of each attribute score h, that is,

$$\begin{aligned} s(h_{k_i})=\frac{1}{n}\sum _{j=1}^{n}s(v_{j_{k_i}}) . \end{aligned}$$
(1)

Note that s(h) becomes a m-dimensional vector for any hop node including a singleton node. Hence, it allows us to compare measuring scores between hop nodes to choose top-k answers.

Now, we define a measure for top-k query on a connected subgraph, that is, a hop node. More precisely, we define a measure function on the m-dimensional attribute score for each hop node. For any m-dimensional vector, we define a measure \(f: {\mathbb {R}}^{m}_{+}\rightarrow {\mathbb {R}}\) for the top-k answer for GTA as

$$\begin{aligned} f(h) = \sum _{i=1}^{m} s(h_i) , \end{aligned}$$
(2)

which is the sum of all attribute scores for a hop node. Thus, GTA measure satisfies

$$\begin{aligned} f(X) \ge f(Y) \quad \text { if } \quad X \ge Y . \end{aligned}$$
(3)

Note that \(X\ge Y\) means that \(X_i \ge Y_i\) for each \(i=1,\ldots ,m\).

Proposition 1

Let A and B be each hop node with size p and q respectively. Assume that \(A \cup B\) is also a hop node. Suppose \(A \cap B =\emptyset ,\) then

$$\begin{aligned} f(A \cup B) \le \max \{f(A),f(B)\} \end{aligned}$$
(4)

Proof

Let \(A=\{v_{A}^1,\ldots ,v_{A}^p\}\) and \(B=\{v_{B}^1,\ldots ,v_{B}^q\}\). Then the attribute scores for the hop nodes s(A) and s(B) can be evaluated as

$$\begin{aligned} s(A)=\frac{1}{p}\sum _{j=1}^{p}s(v_{A}^j)\quad \text {and}\quad s(B)=\frac{1}{q}\sum _{j=1}^{q}s(v_{B}^j), \end{aligned}$$
(5)

respectively. We note that s(A) and s(B) are m-dimensional vectors, say \(s(A)=(A_1,\ldots , A_m)\) and \(s(B)=(B_1,\ldots , B_m)\). Since \(A \cap B=\emptyset \) and \(A \cup B=\{v_{A}^1,\ldots ,v_{A}^p,v_{B}^1,\ldots ,v_{B}^q\}\), the size of \(A \cup B\) is exactly \(p+q\). Hence, its attribute score, m-dimensional vector \(s(A\cup B)\) can be written as

$$\begin{aligned} \begin{aligned} s(A\cup B)&=\frac{1}{p+q}\left( \sum _{j=1}^{p}s(v_{A}^j)+\sum _{j=1}^{q}s(v_{B}^j)\right) \\&= \left( \frac{p\cdot A_1+q\cdot B_1}{p+q},\ldots ,\frac{p\cdot A_m+q\cdot B_m}{p+q} \right) \end{aligned} \end{aligned}$$
(6)

since \(\sum _{j=1}^{p}s(v_{A}^j)=p(A_1,\ldots ,A_m)\) and \(\sum _{j=1}^{q}s(v_{B}^j)=q(B_1,\ldots ,B_m)\). Therefore,

$$\begin{aligned} \begin{aligned} f(A\cup B)&=\sum _{i=1}^{m}\frac{(p\cdot A_i+q\cdot B_i)}{p+q}\\&=\frac{p}{p+q}\sum _{i=1}^{m}A_i+\frac{q}{p+q}\sum _{i=1}^{m}B_i\\&=\frac{p}{p+q}f(A)+\frac{q}{p+q}f(B) . \end{aligned} \end{aligned}$$
(7)

Suppose \(f(A)\ge f(B)\). Then \(f(A)=\max \{f(A),f(B)\}\). Hence,

$$\begin{aligned} \begin{aligned} f(A\cup B)&=\frac{p}{p+q}f(A)+\frac{q}{p+q}f(B)\\&\le \frac{p}{p+q}f(A)+\frac{q}{p+q}f(A)\\&= f(A)=\max \{f(A),f(B)\}. \end{aligned} \end{aligned}$$
(8)

Suppose \(f(A) \le f(B)\). Then \(f(B)=\max \{f(A),f(B)\}\). Similarly,

$$\begin{aligned} \begin{aligned} f(A\cup B)&=\frac{p}{p+q}f(A)+\frac{q}{p+q}f(B)\\&\le \frac{p}{p+q}f(B)+\frac{q}{p+q}f(B)\\&= f(B)=\max \{f(A),f(B)\}. \end{aligned} \end{aligned}$$
(9)

Therefore, \(f(A \cup B) \le \max \{f(A),f(B)\}\). \(\square \)

Let h be top-one answer. Suppose the size of h is two. Then h consists of two singleton hop nodes, say \(h^1\) and \(h^2\). Since \(\displaystyle h=h^1 \cup h^2\) and \(h^1 \cap h^2 = \emptyset \), we can conclude \(f(h) \le \max \{f(h^1),f(h^2)\}\) from the proposition. It implies that top-one answer can be found in the set of singleton hop nodes.

Corollary 1

Top-k answers of GTA are in the set of all hop nodes with hop size less than or equal to k.

Proof

Let h be a top-k answer with hop size n. Suppose \(n > k + 1\). Since a hop node is the set of all vertices of a connected subgraph of G(V, E), there exists a tree H such that whose node set is the same as h. Note that H has \(n-1\) edges. If we delete an edge \(e_j\) in H, then it generates two subtree of H, say \(H^1_j\) and \(H^2_j\). Let \(h^1_j\) and \(h^2_j\) are hop nodes from \(H^1_j\) and \(H^2_j\), respectively. Then \(h^1_j \cap h^2_j=\emptyset \) and \(h = h^1_j \cup h^2_j\). Thus, at least one hope node has bigger measuring score than h and less hop size than h from the proposition.

Hence, we have \(n-1 > k \) hop nodes whose measuring scores are bigger than h. If the hop sizes of all of these hop nodes are less than equal k, then the corollary is proved. If one of the hop size is greater than k, we can do the same argument on that hop node until the hop sizes of all hop nodes are less than equal to k. \(\square \)

From the corollary, we have an upper bound of the hop number for Top-k answers. Thus, we define \({\textit{MaxHop}}\) for the Top-k answers as the following.

Definition 4

(Max Hop) When the answer set of the Top-k answer problem is \(A_k\), then \({\textit{MaxHop}} = max \{ |h|-1 , h \in A_k \}\).

4 Naïve graph threshold algorithm

In this section, we want to see why the threshold algorithm (TA) [13] and the naïve extention of it are not appropriate for Graph environment, where the TA can find the optimal solution without reading the data less than a threshold value obtained from a monotonic function. The preliminary procedure for TA is summarized as follows. Table 1 lists the frequently used notations in this paper.

Table 1 The notations with the description
Full size table
figure a

  • Step 1. Do sorted access in parallel to each of the m sorted lists \(L_i\). As a new object o is seen under the sorted access in some list, do random access to the other lists to find \(p_i(o)\) in every other list \(L_i\). Predicate \(p_i\) determines objects order in \(L_i\). Then compute the score \(F(o)=F(p_1,\ldots ,p_m)\) of object o. If this score is among the k highest scores seen so far, then remember object o and its score F(o) (ties are broken arbitrarily, so that only k objects and their scores are remembered at any time).

  • Step 2. For each list \(L_i\), let \({\overline{p}}_i\) be the score of the last object seen under sorted access. Define the threshold value T to be \(F({\overline{p}}_i,\ldots ,{\overline{p}}_m)\). As soon as at least k objects have been seen whose scores is at least equal to T, then halt.

  • Step 3. Let \(A_k\) be a set containing the k objects that have been seen with the highest scores. The output is then the sorted set \(\{(o,F(o)|o\in A_k)\}\).

When reading each row, you can find the threshold value T as the sum value of the iteration row and find the correct top-2 result (object 1 and 2) without reading the data below the threshold value for each iteration. However, despite the efficiency of the TA algorithm, there is a limit to apply it directly to the graph environment. To solve this problem, we introduce Naïve Graph TA which recognizes each edge as an individual node and apply TA algorithm. After that, the GTA will be presented which can improve the Naïve Graph TA.

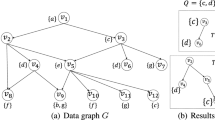
Naïve Threshold Algorithm for Graph (hereinafter NaïveGTA) is a graph top-k algorithm applied on the TA. NaïveGTA solves the problem in the same way as TA by pre-generating all the hop nodes as a single node. For example, Fig. 2 is an example to illustrate the Top-k answer problem of Graph TA in Fig. 2a–d. There are total six nodes with two attribute lists. If we want to find the result of top-3, NaïveGTA algorithm terminates at the \(v_1-v_4\) since there are a total of three or more objects that exceed the threshold value (0.65), as shown in Fig. 2.

Fig. 2
figure 2

An example of NaïveGTA

Full size image

However, since NaïveGTA assumes that all combinations of connection relations are known, the complexity of NaïveGTA is do generate the combinations for all node relations. Assuming that the time complexity of the TA algorithm is O(NaïveGTA(G)) for any graph G, the time complexity for solving the Top-k answer problem using NaïveGTA is as follows. If all the hop graphs generated in an arbitrary graph G are denoted as \(G^h\) and the hop graph generation time is denoted as HopGraphGenTime(G) in the G, the time complexity of NaïveGTA is as follows. O(NaïveGTA(G)) \(=\) O(HopGraphGenTime(G)) \(+\) O(TA(\(G^h\))).

In the case of O(TA(\(G+G^h\))), TA(G) and TA(\(G^h\)) are equal in terms of time complexity because the threshold increase in proportion to the number of newly created hop nodes. If G is a complete graph, then in the worst case, we need to calculate the combination of all nodes, so HopGraphGenTime(G) is as follows.

$$\begin{aligned} \textit{O}({\textsf {HopGraphGenTime}}(G))=\sum _{i=1}^{n}{n\atopwithdelims ()i} \end{aligned}$$

This combination process requires not only an increase in the number of combinations but also a large number of resources and time for the algorithm because the algorithm must store all the combinations in the memory during the procedure.

In other words, for a graph G, the graph top-k query problem is a problem where O(HopGraphGenTime(G)) time itself is already exponential. Therefore, in order to reduce the time complexity of the graph top-k query problem, the hop node generation time must be reduced. In fact, it is not necessary to generate all the hop nodes in advance to solve graph top-k query problem, because it searches only below the threshold value by the optimal condition. Finally, if we find a way to make the combination efficient by reducing the size of \(G^h\), then the time complexity can be replaced by O(TA(G)). In order to reduce the size of the hop graph \(G^h\), the next algorithm proposed in this paper is to limit the size of \(G^h\) by limiting to m. A new data structure called SnakeLink is used to introduce an algorithm that can quickly and efficiently generate \(G^h\).

5 Graph threshold algorithm (GTA)

Table 2 summarizes the notations used in the GTA algorithm.

Table 2 Notations used in the GTA algorithm
Full size table

The biggest problem with NaïveGTA is that as mentioned in Sect. 4, the algorithm can be excuted after finding \(G^h\) including all hop node combinations. There are two main factors that can reduce the computational complexity of the graph top-k query problem.

The first thing is to make \(G^h\) minimize as much, and secondly, the hop node combination should be derived as fast as possible. GTA is a method for generating hop nodes by proceeding with the step of the algorithm in order to reduce the former \(G^h\) and supplemented the disadvantages of NaïveGTA by improving the hop node combining operation to solve the latter problem. The algorithm is described below step by step.

  • Step 1. There is a graph G. Each node attribute will be stored as an ordered list \(L_i\) with m attributes. And find a current top node-set (hereinafter referred to as \(N_{{\textit{top}}}\)) in each list (\(L_1,\ldots ,L_m\)) while sequentially searching for \(L_i\) sorted in parallel. This is to store the objects to be random access in the current iteration. If all the top node-set is saved, delete all the nodes stored in \(N_{{\textit{top}}}\) in \(L_i\). Then, like TA, random access is performed to find the value of all remaining attributes of \(N_{{\textit{top}}}\). When the random access is completed, it is saved in the hop graph set \(G^h\), where \(G^h\) stores both single node and hop node.

  • Step 2. Call the MakeHopNode function, which is a sub-procedure to create the hop graph. We store the gate node-set (\(N_{{\textit{gate}}}\)) using \(N_{{\textit{top}}}\). Then, find the hop node h using \(N_{{\textit{gate}}}\) and \(N_{{\textit{visited}}}\) and put it in \(G^h\). If h is less than or equal to k minus the number of single nodes included in top-k, it is put in \(G^h\) (Theorem 3).

  • Step 3. Modify the threshold T value through \(N_{top}\) as in the case of TA.

  • Step 4. Put the value of \(G^h\) greater than T into the result set \(A_k\).

  • Step 5. In the number of \(A_k\) is larger than k, the algorithm terminates. Otherwise, go back to Step 1 and repeat iteration.

  • Step 6. If there is a candidate hop node-set (a non-permanent node and a connected hop node) that can be included in \(A_k\) after the result \(A_k\) is derived, it can be included in the result set \(A_k\) if both cases are satisfied. First, the score of the hop node must be greater than T. Second, the maximum length of the hop node must be less than or equal to k minus the number of single nodes (Theorem 3).

figure b

The main algorithm of this study, GTA, is in Algorithm 2 which needs two sub-functions Algortihm 3 and Algortihm 4. Algortihm 3 is a function that make a hop graph. Algortihm 4 is a function that finds the candidate hop nodes (\(H_{{\textit{candi}}}\)).

figure c
figure d

Theorem 1

(Top-k bound) When there is a hop node with an arbitrary size k, the hop node can not be ranked higher than the k-th possible highest rank in the top-k answer.

Proof

Let us assume that when there is an arbitrary hop node of size k, it is ranked higher than the k-th in the top-k answer. Since size is k, it is a hop node made up of k nodes. Let’s assume that we create one node from 1 to k and one size increase to make it a k-hop node. When \(|h| = 1\), the maximum possible size in top-k is 1 (one of the two nodes with size 1 is greater than the node with combined size of 2). For \(|h| = 2\), the maximum possible size in top-k is 2 (one of the two nodes with size 1 and 2 is greater than the node with combined size 3). If size is k, the maximum possible size is k, so it can not be ranked higher than k, so it is the opposite of the assumption. Therefore, the node with size k is the highest ranking possible in the top-k answer. \(\square \)

Theorem 2

(Optimal condition—single node bound) arbitrary Graph G(V, E) and the graph top-k answer is obtained from G, at least k single nodes are read during the GTA process. If the value is greater than k in the iteration, k answer set is optimal.

Proof

When there is a graph G, TA is a set of TA solutions, and GTA is a set of GTA solutions such that TA is a subset of GTA (\(\mathrm{TA}\subseteq {\textsf {GTA}}\)). TA arranges each value monotone, so if you read k single nodes, you can naturally obtain at least k top answers. If we can get k solutions in TA, can be obtained. (Since \(TA\subseteq {\textsf {GTA}}\)) In other words, when there is no edge in the graph G, the graph top-k answer problem is the same as a normal TA. When a total of k top answer is obtained, TA will terminate if there are k values larger than the threshold in each iteration. At this time, at least k single nodes should be read. If any edge is connected to G, more nodes that the minimum single node are created in top-k due to the generation of the top node. Since GTA includes TA, the definition above is true. Since the number of top-k answer solutions in the case where there is at least one edge is greater than the number of top-k answer solutions in the case where no edge exists. \(\square \)

Theorem 3

There is a hop graph \(G^h\) from an arbitrary graph G. When will calculate the top-k query on the graph \(G^h,\) the maximum hop node size of the top-k answer set \(|A_k|\) is less than or equal to the followings:

$$\begin{aligned} \arg \max _{h \in A_k}(|h|) \le k -|\text {single nodes} \in A_k| \end{aligned}$$
(10)

Proof

Suppose that we want to find k answer solutions in an arbitrary graph G. In Theorem 1, we proved that k is greater than or equal to \(\arg \max _{h \in A_k}(|h|)\). Therefore, when max-hop (\(G^h\)) of graph G is h, \(k \ge h\). Assume that we select one of the max-hop nodes from \(A_k\). Removes an arbitrary node from the selected hop node. In this case, one of the divided two hop nodes is larger than the existing hop node by Theorem 2. If the score of a single node is larger, a single node is already included in top-k, so a single node in top-k is increased. On the contrary, if the score of the remaining hop node is larger, the remaining nodes are included in top-k and increased Therefore, in the problem of obtaining top-k answers, the difference between the number of single nodes included in k and top-k is always greater than the number of \({\textit{Max Hop}}\). \(\square \)

6 Experiments

We have designed and performed a comprehensive set of experiments to evaluate the search performance of GTA. TA, NaïveGTA, and Star were used as comparison algorithms with GTA. DBLife (3365 nodes, 19,050 arcs) was used as the dataset. Experiments were carried out on the following top-k, number of query size m, graph density, dataset distribution difference, and hop size. Table 3 represents the queries of the experiments.

Table 3 The example of queries
Full size table
Fig. 3
figure 3

Comparison of algorithms execution time according to top-k change and each query

Full size image

The first experiment carried out the algorithm performance for increasing k with the number of hops (|h|) fixed at 3. Figure 3a represents the average execution time with the top-k change from each query. Although there is no significant difference in execution time when |h| is fixed at 3, STAR records an increase as the matrix size increases as the top-k increases. TA algorithm is not affected much by the number of top-k. This is because the TA algorithm determines the result according to the number of query size m rather than the number of data n. The following experiment is the execution time for each query. The execution time is taken to find the top-100 result for each query. Similar to the top-k test results, the graph search algorithms took about 2–3 times more search time than the TA algorithm, but GTA showed the best performance.

The second experiment carried out the algorithm performance for increasing \({\textit{edges}}\) with |h| fixed at 2. In Fig. 4a, in the case of NaïveGTA, it can be seen that the number of edges increases proportionally when making hop nodes. GTA and TA were not significantly affected by edges increase.

Fig. 4
figure 4

Comparison of algorithms execution time according to number of edges and hop size

Full size image

This experiment is a comparison of search speed according to hop size change. In Fig. 4b, in the case of TA, all results have the same time because there is no hop, so it is not affected by hop. NaïveGTA shows that the hop node generation time is greatly increased even when the hop size at 4, and the speed is increased sharply from the hop size at 2. The GTA is not significantly affected by the number of hops, and the performance is even better.

This experiment is a comparison of execution time with data distribution. The experimental result shows that 500, 1500, and 3000 nodes of arbitrary data are generated with three data types (uniform, correlated, anti-correlated) in Fig. 5. The point of interest is that it has the worst performance in uniform data and the best performance in anti-correlated data, which is important. Considering anti-correlated data in two dimensions, we can see that it is concentrated in the threshold part of \(y = -x\) type. This type of data type can quickly derive the TA result compared to other data types because the threshold is quickly lowered without performing many iterations.

Fig. 5
figure 5

Comparison of three data set (Uniform/Correlated/Anti-Correlated)

Full size image
Fig. 6
figure 6

Comparison of the average hop size according to number of edges and nodes

Full size image

This experiment is a comparative experiment on the change of the number of hop nodes according to top-k change. We experimented with two variables (node, edge). In Fig. 6a, we experimented to generate four graphs of 50, 100, 200, and 400 edges in 50 nodes and experimented how the average hop count changes for each graph. As the number of nodes is 50, the number of hops is 1.5 on the average, with a ratio of 1 to 1 for 50 edges. Also, it was not significantly affected by the number of top-k. In edges 100 cases, the ratio of the node to the edge is 1:2 ratio, but it did not respond to top-k. Therefore, we can see that the change of the number of hops according to top-k greatly affected by the dense graph. In Fig. 6b, we experimented with 100 edges with 100 nodes to 3000 nodes. Experimental results show that the average number of hops is maintained at 1 to 3 and the number of nodes is not significantly affected. The experimental results show that the actual average number of hops is significantly smaller than that of \({\textit{Max Hop}}\). This is because the number of hop nodes is reduced each time a singleton node is added to top-k. Also, as the number of arcs increases, the probability of generating a good result set is high even with a small number of hops so that the number of |h| is much smaller than that of Max (k). Figure 7 shows the change of max-hop with increase of dimension m. The random graph is generated and repeated 5 times to show the number of \({\textit{MaxHop}}\) on the graph. When the dimension is less than 10, the number of h increases with the increase of the dimension. In this experiment, we can observe that h is not always smaller than top-k, and that the sensitivity to dimension does not increase much after hop 11. That is, as the arc increases, the number of hops increases finely on the average as the dimension increases as a whole.

Fig. 7
figure 7

Comparison of the average hop size according to number of edges and nodes

Full size image
Fig. 8
figure 8

Comparison of the execution time according to top-k with hop size 4

Full size image

In Fig. 8a, the experiment is the top-k change experiment when |h| is changed to 4 on the experiment. TA was not influenced by the number of hops, so it showed good results and GTA was also not influenced by hop significantly. STAR was also somewhat slower than GTA but generally stable. However, in the case of NaïveGTA, the hop node generation time also increases, and it can be seen that it increases greatly in top-2. In addition, from the top-3 or higher, the result is exponentially increased. Figure 8b shows the performance test when k increases significantly. (top-200 to 1000). In general, all the algorithms except NaïveGTA showed good experimental results even if they proceeded to top-1000 or higher. In the case of NaïveGTA, the speed was greatly increased and was excluded from the experimental results.

7 Conclusion

We present two algorithms, called NaïveGTA and GTA, for solving the Top-k graph search problem with respect to k, dimension, and arc/node changes compared with the existing algorithms. The Top-k graph search problem is bounded by the combination of the number of arcs where all the hops of the arcs should be enumerated.To solve this problem, we prove that \(| h | <\max (d, k)\) and the Top-k graph search problem can be determined by d and k, and the threshold for the maximum hop is quickly decided by |h|. This method not only covers all the hop combinations but also allows sub-graph enumeration without reading all the combinations which is the main difference between NaïveGTA and GTA. We devised a novel algorithm GTA that can effectively solve the Top-k graph search problem for the general graph environment which is the general form of isolated node problems even with a high ratio of arcs such as complete graphs and various dimensions. It can be applied to graph-structured data envirnment regardless of unstructured (ex. Web, Doc) or semi-structured (ex. XML, RDF) or structured (ex. RDBMS) so that the various fields for finding top-k results considering relationships can easily covered such as social networks, patents, citation graphs, web SEO and fake references, etc. In the future the size of the input combination will be increased from the huge graph embeddings, we will tackle the issue by a deep and shallow learning network.