Performance analysis of device-to-device communications underlaying cellular networks

Abstract

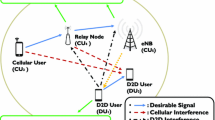
Device-to-device (D2D) communications underlaying cellular networks are considered to be promising communication modes to improve network radio resource efficiency and provide higher transmission data rates to devices close to each other. However, when D2D communications reuse cellular resources, the resulting interference will cause significant performance loss to cellular users. In this paper, the spatial distribution of D2D communication users is modeled as a homogeneous spatial poisson point process. With this assumption, the closed-form expressions of the cumulative distribution functions (CDF) of the uplink interference power from the D2D communications and the signal power from the serving cellular users to the base station are derived, respectively. The approximate CDF of the uplink signal-to-interference-ratio of cellular users is also given in our analysis. More attractively, the analytical results can be used to help design the constraints on the configurations of D2D communications considering the minimum requirements of cellular users. Simulation results validate our analysis. Application examples of the analytical results are also given in this paper.

Appendices: Derivation of the statistical characteristics of the sum of received power

Assume $\varPi _Y$ is an SPPP on $\fancyscript{A}$ with intensity $\lambda$, we will analyze the statistical characteristics of the sum of received power at an arbitrary point $x$ in the two-dimensional plane comprised of all the points in $\varPi _{Y}$.

Since shadow fading is a random variable, it is necessary to form a marked SPPP. Define by $Q_{Y} \in R^{+}$ as the random marking of $\varPi _{Y}$. For any two different points $y_{1}$ and $y_{2}$, $Q_{y_1}$ and $Q_{y_2}$ are independent. The distribution of $Q_{Y}$ is the same for all the points in $\varPi _{Y}$, and $10{\log _{10}}({Q_{Y}}) \sim \mathcal {N}(0,{\sigma ^{2}})$, where $\sigma ^{2}$ is the variance. The probability density function (PDF) is

$$\begin{aligned} {f_{{Q_Y}}}\left( q \right) = \frac{1}{{q \sqrt{\pi a_y} }} \mathtt{e ^{ - \frac{{{{\left( {\ln q} \right) }^2}}}{a_y}}}. \end{aligned}$$

(24)

where $a_y = {2{\beta ^2}{\sigma ^2}}$ and $\beta = \left( {\ln 10} \right) /10$.

The pair $\left( Y,{Q_Y}\right)$ can then be regarded as a random point ${Y^{*}}$ in the product space $\mathbb {C}=\fancyscript{A}\times \mathbb {R}^{+}$. The totality of points ${Y^{*}}$ forms a random countable subset $\varPi _{Y}^{*}=\left\{ {\left( {Y,{Q_Y}} \right) ;Y \in {\varPi _{Y}}} \right\}$ of $\mathbb {C}$. According to the Marking Theorem [19], $\varPi _{Y}^{*}$ is still a SPPP on $\mathbb {C}$, with mean measure ${\mu ^{*}}$ given by

$$\begin{aligned} {\mu ^*}\left( \mathbb {C} \right)&= {\iint \limits _{{\left( y,{Q_y}\right) } \in \mathbb {C}} {{\mu \left( {\mathrm{{d}}y} \right) p\left( {\mathrm{{d}}{Q_y}} \right) }}} \nonumber \\&= {\iint \limits _{(y,{Q_y}) \in {\mathbb {C}}} {{{\lambda \, \mathrm{{d}}y {f_{{Q_Y}}}\left( q\right) \, \mathrm{{d}}q}}}}. \end{aligned}$$

(25)

Define the received power from a transmitter $y$ to the particular receiver $x$ as

$$\begin{aligned} {P_{r,x,y}} = g\left( y,Q_y\right) = {P_{t}} {r_y}^\alpha {Q_y}. \end{aligned}$$

(26)

where $r_y$ is the distance between $y$ and $x$. The sum of the received power is

$$\begin{aligned} {P_\Sigma } = \sum \limits _{y \in {\varPi _Y}} {g\left( y,Q_y\right) }. \end{aligned}$$

(27)

Using Campbell’s Theorem [19], the characteristic function of ${P_\Sigma }$ is

$$\begin{aligned}&\!\!\!{\varPhi _{{P_\Sigma }}} \left( \omega \right) = E \left[ \mathtt{e }^{j\omega {P_\Sigma }}\right] \nonumber \\&\!\!\!\quad = \exp \left[ \;{\iint \limits _{(y,{Q_y}) \in \mathbb {C}} {{\left( \mathtt{e }^{j\omega {g\left( y,Q_y\right) }} - 1 \right) }}{{\mu ^*}\left( {\mathrm{{d}} y,\mathrm{{d}} {Q_y}} \right) }} \right] \nonumber \\&\!\!\!\quad = \exp \left\{ {{E_{{Q_y}}} {\left[ {\int \limits _{{r_y} \in (0,\infty )} { \left( \mathtt{e }^{j\omega {P_{t}} {r_y}^\alpha {Q_y}} - 1\right) 2 \pi \lambda {r_y}\, \mathrm{{d}} {r_y}} } \right] }} \right\} .\nonumber \\ \end{aligned}$$

(28)

Define $u \buildrel \Delta \over = {P_{t}} {r_y}^\alpha {Q_y}$ that falls under the range of $\left( {\infty ,0} \right)$ since $\alpha$ is always negative. With this variable substitution, (28) can be rewritten as

$$\begin{aligned}&{\varPhi _{{P_\Sigma }}} \left( \omega \right) \nonumber \\&\quad = \exp \left\{ \pi {\lambda }{E_{{Q_y}}}\right. \nonumber \\&\quad \quad \left. \times \left[ {\int \limits _{u \in \left( {\infty ,0} \right) } {\left( \mathtt{e ^ {j \omega u} - 1} \right) {{\left( {\frac{1}{{{P_{t}}{Q_y}}}} \right) }^{\frac{2}{\alpha }}}\frac{2}{\alpha }{u^{\frac{2}{\alpha } - 1}}\mathrm{{d}} u} } \right] \right\} \nonumber \\&\quad = \exp \left( {\pi {\lambda }{P_{t}}^{ - \frac{2}{\alpha }} {A_1} {A_2}} \right) . \end{aligned}$$

(29)

where

$$\begin{aligned} A_1= {\int \limits _{u \in \left( {\infty ,0} \right) } {\left( \mathtt{e ^ {j \omega u} - 1} \right) \frac{2}{\alpha }{u^{\frac{2}{\alpha } - 1}}\mathrm{{d}} u} }, \end{aligned}$$

(30)

and

$$\begin{aligned} A_2= {{E_{{Q_y}}}\left[ {{Q_y}^{ - \frac{2}{\alpha }}} \right] }. \end{aligned}$$

(31)

We first simplify $A_1$ as follows.

$$\begin{aligned} A_1&= \int _{0^+}^\infty {\left( \mathtt{e ^ {j \omega u} - 1} \right) \mathrm{{d}} {u^{\frac{2}{\alpha }}}}\nonumber \\&= {\omega ^{ - \frac{2}{\alpha }}} \left[ {j \cos \left( {\frac{\pi }{2} + \frac{\pi }{\alpha }} \right) - \sin \left( {\frac{\pi }{2} + \frac{\pi }{\alpha }} \right) } \right] \mathrm{{\Gamma }} \left( {1 + \frac{2}{\alpha }} \right) \nonumber \\&= - {\omega ^{ - \frac{2}{\alpha }}} \mathtt{e ^{\frac{{j \pi }}{\alpha }}} \mathrm{{\Gamma }} \left( {1 + \frac{2}{\alpha }} \right) . \end{aligned}$$

(32)

where $\mathrm{{\Gamma }} \left( x \right) = \int _0^\infty {{t^{x - 1}} \mathtt{e ^{-t}}dt}$.

In order to simplify $A_2$, the average $k$th power of the log-normal distributed random variable $Q_Y$ is derived as follows.

$$\begin{aligned} E\left[ {{q^k}} \right]&= \int \limits _{m \in {R^ + }} {{q^k} {f_{{Q_Y}}}\left( q \right) \mathrm{{d}} q } \nonumber \\&= \frac{1}{{\sqrt{\pi {a_y}} }} \int _0^{ + \infty } {{q^{k - 1}} {{q^{ - \frac{{\ln q}}{a_y}}}}\mathrm{{d}} q }. \end{aligned}$$

(33)

Defining ${v \buildrel \Delta \over = \ln q}$ ${v \in \left( { - \infty , + \infty } \right) }$, we have

$$\begin{aligned} E\left[ {{q^k}} \right]&= \frac{1}{{\sqrt{\pi {a_y}} }} \int _{ - \infty }^{ + \infty } {\mathtt{e ^{ - \frac{{{v^2}}}{{{a_y}}} + k v}}\mathrm{{d}} v} =\mathtt{e ^{\frac{{{k^2} {a_y}}}{4}}}. \end{aligned}$$

(34)

Substituting (34) in to (31), $A_2$ can be simplified as

$$\begin{aligned} A_2={{E_{{Q_y}}}\left[ {{Q_y}^{ - \frac{2}{\alpha }}} \right] }={\mathtt{e ^{\frac{{{a_y}}}{{{\alpha ^2}}}}}}. \end{aligned}$$

(35)

As a result, the characteristic function is given by

$$\begin{aligned} {\varPhi _{{P_\Sigma }}} \left( \omega \right)&= \exp \left[ { - \pi {\lambda } {P_{t}}^{ - \frac{2}{\alpha }} {\mathtt{e ^{\frac{{{a_y}}}{{{\alpha ^2}}}}}} \mathrm{{\Gamma }} \left( {1 + \frac{2}{\alpha }} \right) \mathtt{e ^{\frac{{j \pi }}{\alpha }}} {\omega ^{ - \frac{2}{\alpha }}}} \right] \nonumber \\&= \exp \left( { - A \mathtt{e ^{\frac{{j \pi }}{\alpha }}} {\omega ^{ - \frac{2}{\alpha }}}} \right) , \end{aligned}$$

(36)

where $A \buildrel \Delta \over = \pi {\lambda } {P_{t}}^{ - \frac{2}{\alpha }} {\mathtt{e ^{\frac{{{a_y}}}{{{\alpha ^2}}}}}} \mathrm{{\Gamma }} \left( {1 + \frac{2}{\alpha }} \right)$.

The laws of probability with characteristic functions given by (36) are the stable laws of exponent $- \frac{2}{\alpha }$ with the restriction of $0 < - \frac{2}{\alpha } < 1$ [24]. Similar to (22) in [23], we give the PDF of the sum of the received power as

$$\begin{aligned} {f_{{P_\Sigma }}}\left( {p;\alpha } \right) {=} \frac{1}{{\pi p}}\sum \limits _{k = 1}^\infty {\frac{{\mathrm{{\Gamma }} \left( {1 - \frac{{2k}}{\alpha }} \right) }}{{k!}} {\left( {\frac{A}{{{p^{ - \frac{2}{\alpha }}}}}} \right) ^{k}} \sin k\pi \left( {1 {+} \frac{2}{\alpha }} \right) }.\nonumber \\ \end{aligned}$$

(37)

Following the inverse Gaussian probability law for $\alpha = -4$, we can have a density given by a closed-form expression. The characteristic function is

$$\begin{aligned} {\varPhi _{{P_\Sigma }}}\left( \omega \right)&= \exp \left[ { - \pi {\lambda } {P_{t}}^{ \frac{1}{2}} \mathtt{e ^{\frac{{{a_y}}}{{16}}}} \mathrm{{\mathrm{{\Gamma }}}} \left( \frac{1}{2}\right) \mathtt{e ^{ - \frac{{j \pi }}{4}}}{\omega ^{\frac{1}{2}}}} \right] \nonumber \\&= \exp \left[ { - \pi \sqrt{\frac{\pi }{2}} \left( {1 - j} \right) \left( \lambda \sqrt{{P_{t}}} \mathtt{e ^{\frac{{{a_y}}}{{16}}}}\right) \sqrt{\omega }} \right] . \end{aligned}$$

(38)

The PDF and CDF of $P_\Sigma$ are given by

$$\begin{aligned} {f_{P_\Sigma }}\left( p \right) = \frac{\pi }{2} \lambda \sqrt{{P_{t}}} \mathtt{e ^{\frac{{{a_y}}}{{16}}}} {p^{ - \frac{3}{2}}} \mathtt{e ^{ - \frac{{{\pi ^3} \lambda ^2 {P_{t}} \mathtt{e ^{\frac{{{a_y}}}{{8}}}}}}{{4 p}}}} \end{aligned}$$

(39)

and

$$\begin{aligned} {F_{P_\Sigma }}\left( p \right) = \mathrm{{erfc}}\left( {\frac{{{\pi ^{\frac{3}{2}}} \lambda \sqrt{{P_{t}}} \mathtt{e ^{\frac{{{a_y}}}{{16}}}} }}{{2\sqrt{p} }}} \right) , \end{aligned}$$

(40)

respectively, where $\mathrm{{erfc}}\left( x \right) = 1-\frac{2}{{\sqrt{\pi }}} \int _0^x {\mathtt{e ^{ - {t^2}}}dt}$.