Skip to main content
SpringerLink
Log in

An analysis of nonstationary coupled queues

  • Published:
Telecommunication Systems Aims and scope Submit manuscript

Abstract

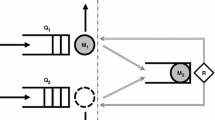
We consider a two dimensional time varying tandem queue with coupled processors. We assume that jobs arrive to the first station as a non-homogeneous Poisson process. When each queue is non-empty, jobs are processed separately like an ordinary tandem queue. However, if one of the processors is empty, then the total service capacity is given to the other processor. This problem has been analyzed in the constant rate case by leveraging Riemann Hilbert theory and two dimensional generating functions. Since we are considering time varying arrival rates, generating functions cannot be used as easily. Thus, we choose to exploit the functional Kolmogorov forward equations (FKFE) for the two dimensional queueing process. In order to leverage the FKFE, it is necessary to approximate the queueing distribution in order to compute the relevant expectations and covariance terms. To this end, we expand our two dimensional Markovian queueing process in terms of a two dimensional polynomial chaos expansion using the Hermite polynomials as basis elements. Truncating the polynomial chaos expansion at a finite order induces an approximate distribution that is close to the original stochastic process. Using this truncated expansion as a surrogate distribution, we can accurately estimate probabilistic quantities of the two dimensional queueing process such as the mean, variance, and probability that each queue is empty.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Askey, R., & Wilson, J. (1985). Some basic hypergeometric orthogonal polynomials that generalize Jacobi polynomials. Memoirs of the American Mathematical Society, 54, 1–55.

    Article  Google Scholar 

  2. Andradottir, S., Ayhan, H., & Down, D. (2001). Server assignment policies for maximizing the steady state throughput of finite state queueing systems. Management Science, 47, 1421–1439.

    Article  Google Scholar 

  3. Blanc, J. P. C. (1988). A numerical study of a coupled processor model. Computer Performance and Reliability, 2, 289–303.

    Google Scholar 

  4. Blanc, J. P. C., Iasnogorodski, R., & Nain, Ph. (1988). Analysis of the \(M/G//1 \rightarrow / M/1\) Model. Queueing Systems, 3, 129–156.

    Article  Google Scholar 

  5. Boxma, O., & Ivanovs, J. (2013). Two coupled Levy queues with independent input. Stochastic Systems, 3(2), 574–590.

    Article  Google Scholar 

  6. Cameron, R., & Martin, W. (1947). The orthogonal development of non-linear functionals in series of Fourier-Hermite functionals. Annals of Mathematics, 48, 385–392.

    Article  Google Scholar 

  7. Cohen, J. W., & Boxma, O. (2000). Boundary Value Problems in Queueing System Analysis. Oxford: Elsevier.

    Google Scholar 

  8. Engblom, S., & Pender, J. (2014). Approximations for the Moments of Nonstationary and State Dependent Birth-Death Queues. Cornell University. Available at: http://www.columbia.edu/~jp3404

  9. Fayolle, G., & Iasnogorodski, R. (1979). Two Coupled Processors: The reduction to a Riemann-Hilbert Problem. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete, 47, 325–351.

    Article  Google Scholar 

  10. Knessl, C., & Morrison, J. A. (2003). Heavy traffic analysis of two coupled processors. Queueing Systems, 30, 173–220.

    Article  Google Scholar 

  11. Knessl, C. (1991). On the diffusion approximation to two parallel queues with processor sharing. IEEE Trans on Automatic Control, 30, 173–220.

    Google Scholar 

  12. Konheim, A. G., Meilijson, I., & Melkman, A. (1981). Processor sharing of two parallel lines. Journal of Applied Probability, 18, 952–956.

    Article  Google Scholar 

  13. van Leeuwaarden, J., & Resing, J. A. C. (2005). Tandem queue with coupled processors: Computational issues. Queueing Systems, 50, 29–52.

    Article  Google Scholar 

  14. Mandelbaum, A., Massey, W. A., & Reiman, M. (1998). Strong approximations for Markovian service networks. Queueing Systems, 30, 149–201.

    Article  Google Scholar 

  15. Massey, W. A., & Pender, J. (2011). Skewness variance approximation for dynamic rate multi-server queues with abandonment. Performance Evaluation Review, 39, 74–74.

    Article  Google Scholar 

  16. Massey, W. A., & Pender, J. (2013). Gaussian skewness approximation for dynamic rate multi-server queues with abandonment. Queueing Systems, 75, 243–277.

    Article  Google Scholar 

  17. Massey, W. A., & Pender, J. (2014). Approximating and Stabilizing Dynamic Rate Jackson Networks with Abandonment. Cornell University, . Available at: http://www.columbia.edu/~jp3404

  18. Osogami, T., Harcol-Balter, M., & Scheller-Wolf, A. (2003). Analysis of cycle stealing with switching cost. ACM Sigmetrics, 31, 184–195.

    Article  Google Scholar 

  19. Ogura, H. (1972). Orthogonal functionals of the Poisson process. IEEE Transactions on Information Theory, 18, 473–481.

    Article  Google Scholar 

  20. Pender, J. (2014). Gram Charlier expansions for time varying multiserver queues with abandonment. SIAM Journal of Applied Mathematics, 74(4), 1238–1265.

    Article  Google Scholar 

  21. Pender, J. (2013). Laguerre Polynomial Approximations for Nonstationary Queues, Cornell University. Available at: http://www.columbia.edu/~jp3404

  22. Pender, J. (2015). Nonstationary loss queues via cumulant moment approximations, Cornell University. Probability in Engineering and Informational Sciences, 29(1), 27–49.

    Article  Google Scholar 

  23. Pender, J. (2014). Sampling the Functional Forward Equations: Applications to Nonstationary Queues. Cornell University. Technical Report. Available at: http://www.columbia.edu/~jp3404

  24. Pender, J. (2014). Gaussian Approximations for Nonstationary Loss Networks. Cornell University. Technical Report. Available at: http://www.columbia.edu/~jp3404

  25. Resing, J., & Ormeci, L. (2003). A tandem queueing model with coupled processors. Operations Research Letters, 31, 383–389.

    Article  Google Scholar 

  26. Stein, C. M. (1986). Approximate Computation of Expectations (Vol. 7)., Lecture Notes Monograph Series Hayward: Institute of Mathematical Statistics.

  27. Wright, P. E. (1992). Two parallel processors with coupled inputs. Advances in Applied Probability, 24, 986–1007.

    Article  Google Scholar 

  28. Xiu, D., & Karniadakis, G. E. (2002). The Wiener-Askey polynomial chaos for stochastic differential equations. SIAM Journal on Scientific Computing, 24(2), 619–644.

    Article  Google Scholar 

Download references

Acknowledgments

This work is partially supported by a Ford Foundation Fellowship and Cornell University.

Author information

Authors and Affiliations

  1. School of Operations Research and Information Engineering, Cornell University, Ithaca, USA

    Jamol Pender

Authors
  1. Jamol Pender
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jamol Pender.

Appendix

Appendix

1.1 Hermite polynomials

Lemma 5.1

(Stein [26]). The random variable \(X\) is Gaussian\((0,1)\) if and only if

$$\begin{aligned} E\left[ X \cdot f(X)\right] = E\left[ \frac{d\ }{dX}f(X)\right] , \end{aligned}$$
(5.1)

for all generalized functions \(f\). Moreover, we also have that

$$\begin{aligned} E\left[ h_n(X) \cdot f(X)\right] = E\left[ \frac{d^n\ }{dX^n}f(X)\right] , \end{aligned}$$
(5.2)

where \(h_n(X)\) is the \(n^{th}\) Hermite polynomial.

Let \(X\) and \(Y\) be two i.i.d Gaussian(0,1) random variables (Fig. 8).

Fig. 8
figure 8

Simulated mean and variance (Left). Simulated Skewness and Kurtosis (Right)

Full size image

Proposition 5.2

Any \(L^2\) function can be written as an infinite sum of Hermite polynomials of \(X\), i.e.

and

$$\begin{aligned} \mathrm {Cov}[f(X), g(X,Y)]= & {} \sum ^{\infty }_{m=1} \frac{1}{m!} E\left[ \frac{\partial ^{m}f}{\partial ^m X }(X) \right] \\&\cdot ~E\left[ \frac{\partial ^{m}g}{\partial ^m X }(X,Y) \right] \\ \end{aligned}$$

1.2 Calculation of expectation and covariance terms

We define \(\varphi \) and \(\Phi \) to be the density and the cumulative distribution functions, for \(X\) respectively, where

$$\begin{aligned} \varphi (x)\equiv & {} \frac{1}{\root \of {2\pi }} e^{-x^2/2}, \ \ \ \Phi (x) \equiv \int _{-\infty }^x \varphi (y)\, dy,\ \ \text{ and } \nonumber \\ \overline{\Phi }(x)\equiv & {} 1-\Phi (x)= \int _{x}^{\infty } \varphi (y)\ dy. \end{aligned}$$
(5.3)

We begin with some of the simpler expectation terms that only involve the evaluation of the Gaussian tail cdf.

$$\begin{aligned} E[\{ X > \chi _1 \}]= & {} {\mathbb {P}}\left( X > \chi _1 \right) = \overline{\Phi }\left( \chi _1 \right) \\ E[\{ X \cdot \cos \theta + Y \cdot \sin \theta > \chi _2 \}]= & {} {\mathbb {P}}\left( Z > \chi _2 \right) = \overline{\Phi }\left( \chi _2 \right) \end{aligned}$$

Now we use the previous proposition to derive the following expectations. Using the \(L^2\) expansion of the function, we get an infinite series representation for the first line. To move from the second to the third line, we use the fact that the function \(\{ Q_1 > 0 \}\) does not depend on the function \(Y\). Lastly, we use the Hermite polynomial generalization of Stein’s lemma (Fig. 9).

$$\begin{aligned}&\mathrm {E}\left[ \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \sum ^{\infty }_{m=0} \sum ^{\infty }_{n=0} \frac{1}{m!n!} E\left[ \frac{\partial ^{n+m}}{\partial ^m X \partial ^n Y} \{ Q_1 > 0 \} \right] \\&\qquad \cdot ~E\left[ \frac{\partial ^{n+m}}{\partial ^m X \partial ^n Y} \{ Q_2 > 0 \} \right] \\&\quad = \sum ^{\infty }_{m=0} \frac{1}{m!} E\left[ \frac{\partial ^{m}}{\partial ^m X } \{ Q_1 > 0 \} \right] \cdot E\left[ \frac{\partial ^{m}}{\partial ^m X } \{ Q_2 > 0 \} \right] \\&\qquad \mathrm {(since \ Q_1 \ does \ not \ depend \ on \ Y)}\\&\quad = \overline{\Phi }( \chi _1) \cdot \overline{\Phi }( \chi _2) + \phi (\chi _1) \cdot \phi (\chi _2) \cdot \sum ^{\infty }_{m=1} \frac{1}{m!} \\&\qquad \cdot ~h_{m-1}(\chi _1) \cdot h_{m-1}(\chi _2) \cdot \cos ^{m} \theta . \end{aligned}$$
Fig. 9
figure 9

Simulated variance vs. GVA variance of queue 1 (Left). Simulated variance vs. GVA variance of queue 2 (Right)

Full size image

The following two expectations can be calculated easily using the previous calculations.

$$\begin{aligned}&\mathrm {E}\left[ \{ Q_1 > 0 \} \cdot \{ Q_2 \le 0 \} \right] \\&\quad = \mathrm {E}\left[ \{ Q_1 > 0 \} \right] - \mathrm {E}\left[ \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad =\overline{\Phi }( \chi _1) - \overline{\Phi }( \chi _1) \cdot \overline{\Phi }( \chi _2) - \phi (\chi _1) \cdot \phi (\chi _2) \\&\qquad \cdot \sum ^{\infty }_{m=1} \frac{1}{m!} \cdot h_{m-1}(\chi _1) \cdot h_{m-1}(\chi _2) \cdot \cos ^{m} \theta \\&\mathrm {E}\left[ \{ Q_1 \le 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \mathrm {E}\left[ \{ Q_2 > 0 \} \right] - \mathrm {E}\left[ \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad =\overline{\Phi }( \chi _2) - \overline{\Phi }( \chi _1) \cdot \overline{\Phi }( \chi _2) - \phi (\chi _1) \cdot \phi (\chi _2) \\&\qquad \cdot \sum ^{\infty }_{m=1} \frac{1}{m!} \cdot h_{m-1}(\chi _1) \cdot h_{m-1}(\chi _2) \cdot \cos ^{m} \theta \end{aligned}$$

Now we begin the calculation of the covariance terms with respect to the first queue length. From the first line to the second we use the property that covariances are invariant to constants. Then, we use the Hermite polynomial expansion property and the Hermite polynomial generalization of Stein’s lemma once again (Fig. 10).

$$\begin{aligned}&\mathrm {Cov}\left[ Q_1, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \mathrm {Cov}\left[ q_1 + \sqrt{v_1} \cdot X, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_1} \cdot \mathrm {Cov}\left[ X, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_1} \cdot \mathrm {E}\left[ X \cdot \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_1} \cdot \sum ^{\infty }_{m=0} \sum ^{\infty }_{n=0} \frac{1}{m!n!} E\left[ \frac{\partial ^{n+m}}{\partial ^m X \partial ^n Y} X \cdot \{ Q_1 > 0 \} \right] \\&\qquad \cdot ~E\left[ \frac{\partial ^{n+m}}{\partial ^m X \partial ^n Y} \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_1} \cdot \sum ^{\infty }_{m=0} \frac{1}{m!} E\left[ \frac{\partial ^{m}}{\partial ^m X } X \cdot \{ Q_1 > 0 \} \right] \\&\qquad \cdot ~E\left[ \frac{\partial ^{m}}{\partial ^m X } \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_1} \cdot \sum ^{\infty }_{m=0} \frac{1}{m!} E\left[ \frac{\partial ^{m}}{\partial ^m X } X \cdot \{ X > \chi _1 \} \right] \\&\qquad \cdot ~E\left[ \frac{\partial ^{m}}{\partial ^m X } \{ X \cdot \cos \theta + Y \cdot \sin \theta > \chi _2 \} \right] \\&\quad = \sqrt{v_1} \cdot \sum ^{\infty }_{m=0} \frac{1}{m!} E\left[ h_m(X) \cdot X \cdot \{ X > \chi _1 \} \right] \\&\qquad \cdot ~E\left[ \frac{\partial ^{m}}{\partial ^m X } \{ X \cdot \cos \theta + Y \cdot \sin \theta > \chi _2 \} \right] \\&\quad = \sqrt{v_1} \cdot \sum ^{\infty }_{m=0} \frac{1}{m!} E\left[ (h_{m+1}(X) + m \cdot h_{m-1}(X) ) \right. \\&\qquad \left. \cdot ~\{ X > \chi _1 \} \right] \cdot E\left[ \frac{\partial ^{m}}{\partial ^m X } \{ X \cdot \cos \theta + Y \cdot \sin \theta > \chi _2 \} \right] \end{aligned}$$
$$\begin{aligned}&\quad = \sqrt{v_1} \cdot \varphi (\chi _1) \cdot \overline{\Phi }(\chi _2) + \sqrt{v_1} \cdot \left( \overline{\Phi }(\chi _1) \right. \\&\qquad \left. +~\chi _1 \cdot \varphi (\chi _1) \right) \cdot \varphi (\chi _2) \cdot \cos \theta \\&\qquad +~\sqrt{v_1} \cdot \sum ^{\infty }_{m=2} \frac{1}{m!} \left( (h_m(\chi _1) + m \cdot h_{m-2}(\chi _1) ) \cdot \varphi (\chi _1) \cdot \right) \\&\qquad \cdot ~E\left[ \frac{\partial ^{m}}{\partial ^m X } \{ X \cdot \cos \theta + Y \cdot \sin \theta > \chi _2 \} \right] \\&\quad = \sqrt{v_1} \cdot \varphi (\chi _1) \cdot \overline{\Phi }(\chi _2) + \sqrt{v_1} \cdot \left( \overline{\Phi }(\chi _1) + \chi _1\right. \\&\qquad \left. \cdot ~\varphi (\chi _1) \right) \cdot \varphi (\chi _2) \cdot \cos \theta \\&\qquad + \sqrt{v_1} \cdot \varphi (\chi _1) \cdot \varphi (\chi _2) \cdot \sum ^{\infty }_{m=2} \frac{1}{m!} \left( h_m(\chi _1) \right. \\&\qquad \left. +~m \cdot h_{m-2}(\chi _1) \right) \cdot h_{m-1}(\chi _2) \cdot \cos ^m \theta \end{aligned}$$

For the next two covariance terms, we use the previous covariance term in the calculation.

$$\begin{aligned}&\mathrm {Cov}\left[ Q_1, \{ Q_1 > 0 \} \cdot \{ Q_2 \le 0 \} \right] \\&\quad =\mathrm {Cov}\left[ Q_1, \{ Q_1 > 0 \} \cdot (1 - \{ Q_2 > 0 \} ) \right] \\&\quad =\mathrm {Cov}\left[ Q_1, \{ Q_1 > 0 \} \right] - \mathrm {Cov}\left[ Q_1, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \mathrm {Cov}\left[ \sqrt{v_1} \cdot X, \{ X > \chi _1 \} \right] - \mathrm {Cov}\left[ \sqrt{v_1} \cdot X, \{ X > \chi _1 \}\right. \\&\qquad \left. \cdot ~\{ X \cdot \cos \theta + Y \cdot \sin \theta > \chi _2 \} \right] \\&\quad = \sqrt{v_1} \cdot \varphi ( \chi _1) - \sqrt{v_1} \cdot \mathrm {Cov}\left[ X, \{ X > \chi _1 \} \right. \\&\qquad \left. \cdot ~\{ X \cdot \cos \theta + Y \cdot \sin \theta > \chi _2 \} \right] \\&\quad = \sqrt{v_1} \cdot \varphi ( \chi _1) - \sqrt{v_1} \cdot \varphi (\chi _1) \cdot \overline{\Phi }(\chi _2)\\&\qquad - \sqrt{v_1} \cdot \left( \overline{\Phi }(\chi _1) + \chi _1 \cdot \varphi (\chi _1) \right) \cdot \varphi (\chi _2) \cdot \cos \theta \\&\qquad - \sqrt{v_1} \cdot \varphi (\chi _1) \cdot \varphi (\chi _2) \cdot \sum ^{\infty }_{m=2} \frac{1}{m!} \left( h_m(\chi _1)\right. \\&\qquad \left. +~m \cdot h_{m-2}(\chi _1) \right) \cdot h_{m-1}(\chi _2) \cdot \cos ^m \theta \\&\quad = \ \sqrt{v_1} \cdot \varphi (\chi _1) \cdot \Phi (\chi _2) - \sqrt{v_1} \cdot \left( \overline{\Phi }(\chi _1) + \chi _1 \cdot \varphi (\chi _1) \right) \\&\qquad \cdot ~\varphi (\chi _2) \cdot \cos \theta \\&\qquad - \sqrt{v_1} \cdot \varphi (\chi _1) \cdot \varphi (\chi _2) \cdot \sum ^{\infty }_{m=2} \frac{1}{m!} \left( h_m(\chi _1) \right. \\&\qquad \left. +~m \cdot h_{m-2}(\chi _1) \right) \cdot h_{m-1}(\chi _2) \cdot \cos ^m \theta \\&\mathrm {Cov}\left[ Q_1, \{ Q_1 \le 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad =\mathrm {Cov}\left[ Q_1, (1- \{ Q_1 > 0 \} ) \cdot \{ Q_2 > 0 \} \right] \\&\quad =\mathrm {Cov}\left[ Q_1, \{ Q_2 > 0 \} \right] - \mathrm {Cov}\left[ Q_1, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad =\mathrm {Cov}\left[ \sqrt{v_1} \cdot X, \{ Q_2 > 0 \} \right] - \mathrm {Cov}\left[ \sqrt{v_1} \cdot X, \{ Q_1 > 0 \} \right. \\&\left. \qquad \cdot ~\{ Q_2 > 0 \} \right] \\&\quad =\sqrt{v_1} \cdot \varphi (\chi _2) \cdot \cos \theta -\sqrt{v_1} \cdot \varphi (\chi _1) \cdot \overline{\Phi }(\chi _2) \\&\qquad - \sqrt{v_1} \cdot \left( \overline{\Phi }(\chi _1) + \chi _1 \cdot \varphi (\chi _1) \right) \cdot \varphi (\chi _2) \cdot \cos \theta \\&\qquad - \sqrt{v_1} \cdot \varphi (\chi _1) \cdot \varphi (\chi _2) \cdot \sum ^{\infty }_{m=2} \frac{1}{m!} \left( h_m(\chi _1) \right. \\&\qquad \left. +~m \cdot h_{m-2}(\chi _1) \right) \cdot h_{m-1}(\chi _2) \cdot \cos ^m \theta \end{aligned}$$

Now we begin the calculation of the covariance terms with respect to the second queue length. From the first line to the second we use the property that covariances are invariant to constants. Then, we use the Hermite polynomial expansion property and the Hermite polynomial generalization of Stein’s lemma once again.

$$\begin{aligned}&\mathrm {Cov}\left[ Q_2, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \mathrm {Cov}\left[ \sqrt{v_1} \cdot X, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_2} \cdot \mathrm {Cov}\left[ X \cdot \cos \theta + Y \cdot \sin \theta , \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_2} \cdot \cos \theta \cdot \mathrm {Cov}\left[ X, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\qquad + \sqrt{v_2} \cdot \sin \theta \cdot \mathrm {Cov}\left[ Y, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_2} \cdot \cos \theta \cdot \mathrm {Cov}\left[ X, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] + \sqrt{v_2} \\&\qquad \cdot \sin \theta \cdot \sum ^{\infty }_{m=0} \sum ^{\infty }_{n=0} \frac{1}{m!n!} E\left[ \frac{\partial ^{n+m}}{\partial ^m X \partial ^n Y} Y \cdot \{ Q_1 > 0 \} \right] \\&\qquad \cdot E\left[ \frac{\partial ^{n+m}}{\partial ^m X \partial ^n Y} \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_2} \cdot \cos \theta \cdot \mathrm {Cov}\left[ X, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\qquad + \sqrt{v_2} \cdot \sin \theta \cdot \sum ^{\infty }_{m=0} \frac{1}{m!} E\left[ \frac{\partial ^{1+m}}{\partial ^m X \partial Y} Y \cdot \{ Q_1 > 0 \} \right] \\&\qquad \cdot ~E\left[ \frac{\partial ^{1+m}}{\partial ^m X \partial Y} \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_2} \cdot \cos \theta \cdot \mathrm {Cov}\left[ X, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\qquad + \sqrt{v_2} \cdot \sin \theta \cdot \left( \overline{\Phi }(\chi _1) \cdot \varphi (\chi _2) \cdot \sin \theta \right) + \sqrt{v_2} \\&\qquad \cdot \sin \theta \cdot \left( \varphi (\chi _1) \cdot \chi _2 \cdot \varphi (\chi _2) \cdot \sin \theta \cdot \cos \theta \right) \\&\qquad + \sqrt{v_2} \cdot \sin \theta \cdot \sum ^{\infty }_{m=2} \frac{1}{m!} E\left[ \frac{\partial ^{m}}{\partial ^m X } \{ X > \chi _1 \} \right] \\&\qquad \cdot ~E\left[ \frac{\partial ^{m}}{\partial ^m X } \delta _{\chi _2}(X\cdot \cos \theta + Y\cdot \sin \theta ) \right] \\&\quad = \sqrt{v_2} \cdot \cos \theta \cdot \mathrm {Cov}\left[ X, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\qquad + \sqrt{v_2} \cdot \sin \theta \cdot \left( \overline{\Phi }(\chi _1) \cdot \varphi (\chi _2) \cdot \sin \theta \right) + \sqrt{v_2} \cdot \sin \theta \\&\qquad \cdot \left( \varphi (\chi _1) \cdot \chi _2 \cdot \varphi (\chi _2) \cdot \sin \theta \cdot \cos \theta \right) \\&\qquad + \sqrt{v_2} \cdot \sin \theta \cdot \sum ^{\infty }_{m=2} \frac{1}{m!} \varphi (\chi _1) \cdot h_{m-1}(\chi _1) \cdot \varphi (\chi _2) \\&\qquad \cdot ~h_{m}(\chi _2) \cdot \sin \theta \cdot \cos ^m \theta \end{aligned}$$

Lastly, for the next two covariance terms, we use the previous covariance term in the calculation.

$$\begin{aligned}&\mathrm {Cov}\left[ Q_2, \{ Q_1 > 0 \} \cdot \{ Q_2 \le 0 \} \right] \\&\quad = \mathrm {Cov}\left[ Q_2, \{ Q_1 > 0 \} \cdot (1 - \{ Q_2 > 0 \} ) \right] \\&\quad = \mathrm {Cov}\left[ Q_2, \{ Q_1 > 0 \} \right] - \mathrm {Cov}\left[ Q_2, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \}\right] \\&\quad = \sqrt{v_2} \cdot \mathrm {Cov}\left[ X \cdot \cos \theta + Y \cdot \sin \theta , \{ Q_1 > 0 \} \right] - \sqrt{v_2} \\&\qquad \cdot ~\mathrm {Cov}\left[ X \cdot \cos \theta + Y \cdot \sin \theta , \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_2} \cdot \cos \theta \cdot \varphi (\chi _1) - \sqrt{v_2} \cdot \mathrm {Cov}\left[ X \cdot \cos \theta \right. \\&\qquad \left. + Y \cdot \sin \theta , \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\mathrm {Cov}\left[ Q_2, \{ Q_1 \le 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \mathrm {Cov}\left[ Q_2, ( 1- \{ Q_1 > 0 \} ) \cdot \{ Q_2 > 0 \} \right] \\&\quad = \mathrm {Cov}\left[ Q_2, \{ Q_2 > 0 \} \right] - \mathrm {Cov}\left[ Q_2, \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_2} \cdot \mathrm {Cov}\left[ X \cdot \cos \theta + Y \cdot \sin \theta , \{ Q_2 > 0 \} \right] - \sqrt{v_2}\\&\qquad \cdot \, \mathrm {Cov}\left[ X \cdot \cos \theta + Y \cdot \sin \theta , \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \\&\quad = \sqrt{v_2} \cdot \varphi (\chi _2) - \sqrt{v_2} \cdot ~\mathrm {Cov}\left[ X \cdot \cos \theta + Y \right. \\&\qquad \left. \cdot \sin \theta , \{ Q_1 > 0 \} \cdot \{ Q_2 > 0 \} \right] \end{aligned}$$
Fig. 10
figure 10

Simulated probability of emptiness of queue 1 (Left). Simulated probability of emptiness of queue 2 (Right)

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pender, J. An analysis of nonstationary coupled queues. Telecommun Syst 61, 823–838 (2016). https://doi.org/10.1007/s11235-015-0039-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11235-015-0039-0

Keywords

Search

Navigation