Skip to main content

Advertisement

SpringerLink
Log in

On the performance of double resolution ADC receivers for massive MIMO relaying systems

  • Published:
Telecommunication Systems Aims and scope Submit manuscript

Abstract

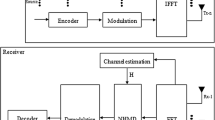
High power consumption and hardware cost are the two challenges for practical massive MIMO systems. One promising solution is to employ low resolution analog to digital converter (ADC). In this paper, massive MIMO relaying systems are investigated with double resolution ADCs at base station receiver, where some antennas are connected to low resolution ADCs, while the rest of the antennas are connected to high resolution ADCs. Closed form expression for uplink spectral efficiency (SE) is derived using the maximum ratio combining receiver assuming perfect channel state information. Some asymptotic analysis is discussed to explore the effects of system parameters on SE such as; the number of receive antennas, ADC quantization bits, user transmit power and the rate of high precision ADC in double resolution ADC structure. Moreover, energy efficiency with some system parameters is studied. It is shown that the performance wastage owing to low precision ADCs can be recompensed by growing the number of receive antennas \( \varvec{N} \), following a logarithmic scaling law instead of increasing the transmit power at both of source and relay. The double resolution ADCs can achieve a better tradeoff between power consumption and SE when using 4 quantization bits. By using only around 30 antennas, the double resolution ADCs achieves its optimal energy efficiency for selecting system parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Yang, A., Xing, W., Fei, Z., & Kuang, J. (2016). Performance analysis for uplink massive MIMO systems with a large and random number of UEs. Science China Information Sciences,59(2), 022312:1–022312:9.

    Article  Google Scholar 

  2. Bjornson, E., Larsson, E., & Marzetta, T. (2016). Massive MIMO: ten myths and one critical question. IEEE Communications Magazine,54(2), 114–123.

    Article  Google Scholar 

  3. Cui, Q., Yuan, T., & Ni, W. (2017). Energy-efficient two-way relaying under non-ideal power amplifiers. IEEE Transactions on Vehicular Technology,66(2), 1257–1270.

    Article  Google Scholar 

  4. Cui, Q., Zhang, Y., Ni, W., & Kuang, J. (2017). Energy efficiency maximization of full-duplex two-way relay with non-ideal power amplifiers and non-negligible circuit power. IEEE Transactions on Wireless Communications,16, 6264–6278.

    Article  Google Scholar 

  5. Xu, W., Liu, J., & Jin, S. (2017). Spectral and energy efficiency of multi-pair massive MIMO relay network with hybrid processing. IEEE Transactions on Communications,65(9), 3794–3809.

    Article  Google Scholar 

  6. Wang, Q., & Jing, Y. (2017). Performance analysis and scaling law of MRC/MRT relaying with CSI error in multi-pair massive MIMO systems. IEEE Transactions on Wireless Communications,16, 5882–5896.

    Article  Google Scholar 

  7. Said, S., Saad, W., & Shokair, M. (2019). MMSE algorithm based two stages hybrid precoding for millimeter wave massive MIMO systems. Analog Integrated Circuits and Signal Processing Journal,98(3), 565–573.

    Article  Google Scholar 

  8. Wang, B., Dai, L., Hanzo, L., & Gao, X. (2018). Beamspace MIMO noma for millimeter wave communication using lens antenna arrays. In IEEE 86 vehicular technology conference

  9. Méndez-Rial, R., Rusu, C., González-Prelcic, N., Alkhateeb, A., & Heath, R. W., Jr. (2016). Hybrid MIMO architectures for millimeter wave communications: phase shifters or switches? IEEE Access,4(8), 247–267.

    Article  Google Scholar 

  10. Zhang, J., Dai, L., Sun, S., & Wang, Z. (2016). On the spectral efficiency of massive MIMO systems with low-resolution ADCs. IEEE Communications Letters,20(5), 842–845.

    Article  Google Scholar 

  11. Li, Y., Tao, C., Secogranados, G., Mezghani, A., Swindlehurst, A. L., & Liu, L. (2017). Channel estimation and performance analysis of one-bit massive MIMO systems. IEEE Transactions on Signal Processing,65(15), 4075–4089.

    Article  Google Scholar 

  12. Liang, N., & Zhang, W. (2016). Mixed-ADC massive MIMO. IEEE J. Sel. Areas Communication,34(4), 983–997.

    Article  Google Scholar 

  13. Liang, N., & Zhang, W. (2016). Mixed-ADC massive MIMO uplink in frequency-selective channels. IEEE Transactions on Communications,64(11), 4652–4666.

    Article  Google Scholar 

  14. Tan, W., Jin, S., Wen, C., & Jing, Y. (2016). Spectral efficiency of mixed-ADC receivers for massive MIMO systems. IEEE Access,4, 7841–7846.

    Article  Google Scholar 

  15. Zhang, J., Dai, L., He, Z., Jin, S., & Li, X. (2017). Performance analysis of mixed-ADC massive MIMO systems over rician fading channel. IEEE Journal on Selected Areas in Communications,35(6), 1327–1338.

    Article  Google Scholar 

  16. Zhang, T., Wen, C., Jin, S., & Jiang, T. (2016). Mixed-ADC massive MIMO detectors: performance analysis and design optimization. IEEE Trans. Wireless Communication,15(11), 7738–7752.

    Article  Google Scholar 

  17. Pirzadeh, H., & Swindlehurst, A. L. (2018). Spectral effciency of mixed-ADC massive MIMO. IEEE Transactions on Signal Processing,66(13), 3599–3613.

    Article  Google Scholar 

  18. Cui, Q., Lui, Y., Xie, W., & Zhao, Y. (2018). Multi-pair massive MIMO amplify-and-forward relaying system with low-resolution ADCs: performance analysis and power control. Science China Information Sciences,61, 022311:1–022311:18.

    Google Scholar 

  19. Feng, J., Ma, S., Yang, G., & Xia, B. (2017). Power scaling of full-duplex two-way massive MIMO relay systems with correlated antennas and MRC/MRT processing. IEEE Transactions on Wireless Communications,16, 4738–4753.

    Article  Google Scholar 

  20. Pirzadeh, H., & Lee Swindlehurst, A. (2018). Spectral efficiency of mixed ADC massive MIMO. IEEE Transactions on Signal Processing,66(13), 3599–3613.

    Article  Google Scholar 

  21. Mollen, C., Choi, J., Larsson, E. G., & Heath, R. W. (2017). Uplink performance of wideband massive MIMO with one-bit ADCs. IEEE Transactions on Wireless Communications,16(1), 87–100.

    Article  Google Scholar 

  22. Mo, J., Alkhateeb, A., Surra, S., & Heath, R. W. (2017). Hybrid architectures with few-bit ADC receivers: achievable rates and energy-rate tradeoffs. IEEE Transactions on Wireless Communications,16, 2274–2287.

    Article  Google Scholar 

  23. Murmann, B. (2017). ADC performance survey 1997–2016. Accessed on March 2017. http://web.stanford.edu/∼Murmann/ADCsurvey.html.

Download references

Author information

Authors and Affiliations

  1. Nuclear Research Center, Atomic Energy Authority, Cairo, Egypt

    Sahar Said & Sayed El-Araby

  2. Electronic and Electrical Communication Department, Faculty of Electronic Engineering, Menoufia University, Menouf, Egypt

    Waleed Saad & Mona Shokair

  3. Electrical Engineering Department, College of Engineering, Shaqra University, Dawadmi, Ar Riyadh, Saudi Arabia

    Waleed Saad

Authors
  1. Sahar Said
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Waleed Saad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mona Shokair
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Sayed El-Araby
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sahar Said.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A

Appendix A

1.1 Proof of Theorem 1

Proof

We approximate \( \varvec{R}_{\varvec{k}} \) as follows:

$$ R_{k} \approx \frac{1}{2}\log_{2} \left( {1 + \frac{{{\text{E}}(P_{U} \left| {g_{kH}^{\dag } g_{kH} + \alpha g_{kL}^{\dag } g_{kL} } \right|^{2} ) }}{{{\text{E}}\left( {\psi_{1} } \right)}}} \right) $$
(28)

where \( \psi_{1} \) is defined in (12). The Expectation terms are derived term by term.

First: calculate the nominator in (28)

$$ E\left\{ { \left| {g_{kH}^{\dag } g_{kH} + \alpha g_{kL}^{\dag } g_{kL} } \right|^{2} } \right\} = E \left\{ {\left| {g_{kH}^{\dag } g_{kH} } \right|^{2} + 2\alpha g_{kH}^{\dag } g_{kH} g_{kL}^{\dag } g_{kL} + \alpha^{2} \left| {g_{kL}^{\dag } g_{kL} } \right|^{2} } \right\} $$

By using the distribution of \( g_{kH}^{\dag } g_{kH} = {\mathbb{a}}_{k}^{\dag } B_{H}^{\dag } B_{H} {\mathbb{a}}_{k} \) conditionally on \( {\mathbb{a}}_{k} \) and \( B_{H}^{\dag } B_{H} \sim {\mathcal{W}}_{M} \left( {\beta_{R} I_{M} ,N_{H} } \right) \) is Wishart matrix according to [14].

We have \( \left| {g_{kH}^{\dag } g_{kH} } \right|{\mathbb{a}}_{k} = \frac{1}{2}\beta_{R} \left\| {{\mathbb{a}}_{k} } \right\|^{2} \chi_{{2N_{H} }}^{2} \) by utilizing conditional expectation \( E\left\{ {\left| {g_{kH}^{\dag } g_{kH} } \right|^{2} {\mathbb{a}}_{k} } \right\} = \frac{1}{4}\beta_{R}^{2} \left\| {{\mathbb{a}}_{k} } \right\|^{4} E\left\{ {\left( {\chi_{{2N_{H} }}^{2} } \right)^{2} } \right\} = \beta_{R}^{2} \left\| {{\mathbb{a}}_{k} } \right\|^{4} N_{H} \left( {N_{H} + 1} \right) \). Then by using expectation over \( {\mathbb{a}}_{k} \), it produces

$$ E\left\{ {\left| {g_{kH}^{\dag } g_{kH} } \right|^{2} } \right\} = \beta_{R}^{2} \beta_{k}^{2} M\left( {M + 1} \right)N_{H} \left( {N_{H} + 1} \right) $$
(29)

where \( \left\| {{\mathbb{a}}_{k} } \right\|^{2} \) follows gamma distribution \( \Gamma \left( {M,\beta_{k} } \right) \) and \( E \{ \left\| {{\mathbb{a}}_{k} } \right\|^{4} \} = \beta_{k}^{2} M\left( {M + 1} \right) \).

By similarity, \( E \left\{ {\left| {g_{kL}^{\dag } g_{kL} } \right|^{2} } \right\} = \beta_{R}^{2} \beta_{k}^{2} M\left( {M + 1} \right)N_{L} \left( {N_{L} + 1} \right) \) and also

$$ E\left\{ {g_{kH}^{\dag } g_{kH} g_{kL}^{\dag } g_{kL} } \right\} = E\left\{ {Tr \left( {{\mathbb{a}}_{k}^{\dag } B_{H}^{\dag } B_{H} {\mathbb{a}}_{k} {\mathbb{a}}_{k}^{\dag } B_{L }^{\dag } B_{L} {\mathbb{a}}_{k} } \right)} \right\} = Tr (E\left\{ {B_{H}^{\dag } B_{H} } \right\}E\left\{ {{\mathbb{a}}_{k}^{\dag } {\mathbb{a}}_{k} B_{L }^{\dag } B_{L} {\mathbb{a}}_{k} {\mathbb{a}}_{k}^{\dag } } \right\} = \beta_{R} N_{H} Tr \left( {E\left\{ {B_{L}^{\dag } B_{L} } \right\}E\left\{ {{\mathbb{a}}_{k}^{\dag } {\mathbb{a}}_{k} {\mathbb{a}}_{k} {\mathbb{a}}_{k}^{\dag } } \right\}} \right) = \beta_{R}^{2} \beta_{k}^{2} M\left( {M + 1} \right)N_{H} N_{L} $$
(30)

By combining all above results, it produces

$$ E\left\{ { \left| {g_{kH}^{\dag } g_{kH} + \alpha g_{kL}^{\dag } g_{kL} } \right|^{2} } \right\} = \beta_{R}^{2} \beta_{k}^{2} M^{2} \left[ {\left( {N_{H} + \alpha N_{L} } \right)^{2} + N_{H} + \alpha^{2} N_{L} } \right] $$
(31)

Second calculate denominator\( \varvec{E}\left( {\varvec{\psi}_{1} } \right) \)in (28)

\( \psi_{1} \) consists of three terms multi user interference \( I_{1} \), additive Gaussian noise \( I_{2} \) and quantization noise \( I_{3} \).

Calculate \( \varvec{E}\left\{ {\varvec{I}_{1} } \right\} \)

$$ \begin{aligned}\varvec{E}\left\{ {\varvec{I}_{1} } \right\} &= E \left[ {\left| {\varvec{g}_{{\varvec{kH}}}^{\dag } \varvec{g}_{{\varvec{jH}}} + \varvec{\alpha g}_{{\varvec{kL}}}^{\dag } \varvec{g}_{{\varvec{jL}}} } \right|^{2} } \right] \\ &= \varvec{E}\left\{ {\left| {g_{kH}^{\dag } g_{jH} } \right|^{2} + \alpha^{2} \left| {g_{kL}^{\dag } g_{jL} } \right|^{2}} \right. \\ &\quad \left. {+\, \alpha \left( {\varvec{g}_{{\varvec{kH}}}^{\dag } \varvec{g}_{{\varvec{jH}}} \varvec{g}_{{\varvec{jL}}}^{\dag } \varvec{g}_{{\varvec{kL}}} + \varvec{g}_{{\varvec{kL}}}^{\dag } \varvec{g}_{{\varvec{jL}}} \varvec{g}_{{\varvec{jH}}}^{\dag } \varvec{g}_{{\varvec{kH}}} } \right)} \right\}. \end{aligned} $$

By analogues to (30), we have

$$ E\left\{ {Tr\left( {{\mathbb{a}}_{k}^{\dag } B_{H}^{\dag } B_{H} {\mathbb{a}}_{k} {\mathbb{a}}_{j}^{\dag } B_{H}^{\dag } B_{H} {\mathbb{a}}_{k} } \right)} \right\} = \beta_{k} \beta_{j} E\left\{ {Tr\left( {B_{H}^{\dag } B_{H} B_{H}^{\dag } B_{H} } \right)} \right\} = \beta_{R}^{2} \beta_{k} \beta_{j} N_{H} M\left( {N_{H} + M} \right) $$
(32)

By similarity, \( E\left\{ {\varvec{g}_{{\varvec{kl}}}^{\dag } \varvec{g}_{{\varvec{kL}}} \varvec{g}_{{\varvec{jL}}}^{\dag } \varvec{g}_{{\varvec{kL}}} } \right\} = \beta_{R}^{2} \beta_{k} \beta_{j} N_{L} M\left( {N_{L} + M} \right) \) and \( E\left\{ {\varvec{g}_{{\varvec{kH}}}^{\dag } \varvec{g}_{{\varvec{jH}}} \varvec{g}_{{\varvec{jL}}}^{\dag } \varvec{g}_{{\varvec{kL}}} } \right\} = E\left\{ {\varvec{g}_{{\varvec{kL}}}^{\dag } \varvec{g}_{{\varvec{jL}}} \varvec{g}_{{\varvec{jH}}}^{\dag } \varvec{g}_{{\varvec{kH}}} } \right\} = \beta_{R}^{2} \beta_{k} \beta_{j} N_{H} N_{L} M \).

Finally, \( E\left\{ {I_{1} } \right\} \) is given by

$$ E\left\{ {I_{1} } \right\} = M\left[ {\left( {N_{H} + \alpha N_{L} } \right)^{2} + M\left( {N_{H} + \alpha^{2} N_{L} } \right)} \right]P_{U} \beta_{R}^{2} \beta_{k} \mathop \sum \limits_{j \ne k}^{K} \beta_{j} $$
(33)

By utilizing the same procedure of deriving \( E\left\{ {I_{1} } \right\} \), we produce

$$ \varvec{E}\left\{ {\varvec{I}_{2} } \right\} = {\mathbf{E}}\left[ {\varvec{g}_{{\varvec{kH}}}^{\dag } \varvec{B}_{\varvec{H}} + \varvec{\alpha g}_{{\varvec{kL}}}^{\dag } \varvec{B}_{\varvec{L}}^{2} + \frac{1}{{\varvec{G}_{\varvec{R}}^{2} }}\left( {\varvec{g}_{{\varvec{kH}}}^{2} +\varvec{\alpha}^{2} \varvec{g}_{{\varvec{kL}}}^{2} } \right)} \right] =\varvec{\beta}_{\varvec{R}}^{2}\varvec{\beta}_{\varvec{k}} \varvec{M}[\left( {\varvec{N}_{\varvec{H}} + \varvec{\alpha N}_{\varvec{L}} )^{2} + \varvec{M}\left( {\varvec{N}_{\varvec{H}} +\varvec{\alpha}^{2} \varvec{N}_{\varvec{L}} } \right)} \right] + \frac{{\varvec{\beta}_{\varvec{R}}\varvec{\beta}_{\varvec{k}} \varvec{M}}}{{\varvec{G}_{\varvec{R}}^{2} }}\left( {\varvec{N}_{\varvec{H}} +\varvec{\alpha}^{2} \varvec{N}_{\varvec{L}} } \right) $$
(34)

Calculate \( \varvec{E}\left\{ {\varvec{I}_{3} } \right\} \)

We refer to \( mth \) column of \( B_{L} \) with \( b_{m}^{\dag } \) and \( jth \) column of \( A \) with \( {\mathbb{a}}_{j} \) and \( \varvec{I}_{3} = \frac{1}{{\varvec{G}_{\varvec{R}}^{2} }}\varvec{g}_{{\varvec{kL}}}^{\dag } {\mathbf{\mathcal{R}}}_{{\varvec{n}_{\varvec{q}} }} \varvec{g}_{{\varvec{kL}}} \)

\( {\mathbf{E}}\left( {\varvec{I}_{3} } \right) = \frac{1}{{\varvec{G}_{\varvec{R}}^{2} }}\mathop \sum \limits_{{\varvec{m} = 1}}^{{\varvec{N}_{\varvec{L}} }} \varvec{E}\left\{ {\varvec{d}_{\varvec{m}} \left| {b_{m}^{\dag } {\mathbb{a}}_{k} } \right|^{2} } \right\} \) and \( \varvec{d}_{\varvec{m}} \) is the \( \varvec{mth} \) entry of \( {\mathbf{\mathcal{R}}}_{{\varvec{n}_{\varvec{q}} }} \) and is given by

\( d_{m} = \alpha \left( {1 - \alpha } \right)\left( {\varvec{G}_{\varvec{R}}^{2} \varvec{P}_{\varvec{U}} \mathop \sum \limits_{{\varvec{j} = 1}}^{\varvec{K}} b_{m}^{\dag } {\mathbb{a}}_{\varvec{j}} {\mathbb{a}}_{\varvec{j}}^{\dag } \varvec{b}_{\varvec{m}} + \varvec{G}_{\varvec{R}}^{2} b_{m}^{\dag } b_{m} + 1} \right) \) by utilizing \( d_{m} \) in \( {\mathbf{E}}\left( {\varvec{I}_{3} } \right) \), we produce

$$ {\mathbf{E}}\left( {\varvec{I}_{3} } \right) = \alpha \left( {1 - \alpha } \right)\left[ {\mathop \sum \limits_{m = 1}^{{N_{L} }} \left\{ {\left( {P_{U} \mathop \sum \limits_{j = 1}^{k} b_{m}^{\dag } {\mathbb{a}}_{j} } \right) + E_{mk} + \frac{{F_{mk} }}{{\varvec{G}_{\varvec{R}}^{2} }}} \right\}} \right] $$

where

$$ \begin{aligned} & b_{m}^{\dag } {\mathbb{a}}_{j} = E \left\{ {b_{m}^{\dag } {\mathbb{a}}_{k} {\mathbb{a}}_{k}^{\dag } b_{m} b_{m}^{\dag } {\mathbb{a}}_{j} {\mathbb{a}}_{j}^{\dag } b_{m} } \right\} =\varvec{\beta}_{\varvec{R}}^{2}\varvec{\beta}_{\varvec{k}}\varvec{\beta}_{\varvec{j}} \varvec{M}\left( {\varvec{M} + 1} \right) \\ & E_{mk} = E\left\{ {b_{m}^{\dag } {\mathbb{a}}_{k} {\mathbb{a}}_{k}^{\dag } b_{m} b_{m}^{\dag } b_{m} } \right\} =\varvec{\beta}_{\varvec{R}}^{2}\varvec{\beta}_{\varvec{k}} \varvec{M}\left( {\varvec{M} + 1} \right) \\ & F_{mk} = E\left\{ {b_{m}^{\dag } {\mathbb{a}}_{k} {\mathbb{a}}_{k}^{\dag } b_{m} } \right\} = \beta_{R} \beta_{k} MN_{L} \\ \end{aligned} $$

Finally,

$$ \varvec{E}\left( {\varvec{I}_{3} } \right) =\varvec{\alpha}\left( {1 -\varvec{\alpha}} \right)\varvec{\beta}_{\varvec{R}}^{2}\varvec{\beta}_{\varvec{k}} \varvec{N}_{\varvec{L}} \varvec{M}^{2} \left[ {\varvec{P}_{\varvec{U}} \left( {\varvec{\beta}_{\varvec{k}} + \mathop \sum \limits_{{\varvec{j} = 1}}^{\varvec{K}}\varvec{\beta}_{\varvec{j}} } \right) + 1} \right] + \frac{{\varvec{\alpha}\left( {1 -\varvec{\alpha}} \right)\varvec{\beta}_{\varvec{R}}\varvec{\beta}_{\varvec{k}} \varvec{N}_{\varvec{L}} \varvec{M}}}{{\varvec{G}_{\varvec{R}}^{2} }} $$
(35)

By combining (31), (33), (34), (35) into (28) with some parameters \( N = {\Re }M \),\( N_{H} = \kappa N \) and \( N_{L} = \left( {1 - \kappa } \right)N \),we complete the proof.□

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Said, S., Saad, W., Shokair, M. et al. On the performance of double resolution ADC receivers for massive MIMO relaying systems. Telecommun Syst 73, 143–154 (2020). https://doi.org/10.1007/s11235-019-00591-7

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11235-019-00591-7

Keywords

Search

Navigation