Schedulability analysis of a graph-based task model for mixed-criticality systems

Abstract

We present a new graph-based real-time task model that can specify complex job arrival patterns and global state-based mode switching. The mode switching is of a mixed-criticality style, meaning that it allows immediate changes to the parameters of active jobs upon mode switches. The resulting task model generalizes previously proposed task graph models as well as mixed-criticality (sporadic) task models; the merging of these mutually incomparable modeling paradigms allows formulation of new types of tasks. A sufficient schedulability analysis for EDF on preemptive uniprocessors is developed for the proposed model.

Appendices

Appendix 1: Some preliminary experiments

1.1 Motivation

It is possible to model many different types of systems using MS-DRT, but at this stage we find it generally difficult to quantitatively evaluate the effectiveness of both the modeling formalism itself and the proposed schedulability analysis, because there is little to directly compare with. Here we try to illustrate the effectiveness of our approach on a restricted set of systems that address a common concern voiced about mixed-criticality scheduling, namely the usual assumption that low-criticality tasks are dropped upon a switch to a higher criticality mode. Often, it is instead desirable to guarantee a minimal quality of service (QoS) to the low-criticality tasks even after a mode switch.

There have been some attempts to solve this in the context of sporadic mixed-criticality tasks by allowing low-criticality tasks to continue executing in the higher criticality mode, but with new parameters (see, e.g., Burns and Baruah 2013; Ekberg and Yi 2014). In these works, low-criticality tasks are essentially treated the same as high-criticality tasks in the sense that they are immediately given new parameters upon a mode switch. Contrary to the high-criticality tasks that typically get worsened parameters (e.g., increased execution times) in the new mode, low-criticality tasks are changed to have a smaller impact on the system, for example by decreasing their execution times or increasing their periods. The motivation for doing so is that if such a system is schedulable, it will provide some QoS guarantees for low-criticality tasks even in the higher criticality mode.

However, we argue that using such an approach will unnecessarily limit schedulability. The reason is that it makes the transitional periods after mode switches harder to successfully schedule. The major challenge in guaranteeing the schedulability of a mixed-criticality system is to show that all jobs that are active shortly after a mode switch will meet their deadlines, in particular the carry-over jobs. If also the low-criticality tasks can have carry-over jobs, ensuring schedulability becomes significantly harder. At the same time, we argue that low-criticality tasks do not need to be treated the same as those of higher criticality simply to provide some QoS in the new mode. The mode switch protocol used for the high-criticality tasks—to immediately change the parameters, including those of active jobs—is, after all, quite extreme. It was designed to make sure that critical tasks will continue to function without any delay whatsoever even in the face of invalid parameter estimates. Instead, by simply pausing low-criticality tasks for a short period of time after a mode switch, before restarting them with less intensive parameters, we can achieve almost the same QoS guarantees without sacrificing schedulability.

Tasks that pause activity for a while after a mode switch are easily modeled with MS-DRT, for example as task $\tau _{2}$ of Example 1. In this evaluation we will compare three different types of low-criticality tasks: those without QoS guarantees in the high-criticality mode; those with basic guarantees as proposed by Burns and Baruah (2013) and Ekberg and Yi (2014); and those that introduce a small delay after a mode switch before restarting. These different types of tasks are shown in Fig. 10, together with the standard type of high-criticality task that they will be mixed with.

Fig. 10

A standard high-criticality task and three different types of low-criticality tasks

1.2 Task set generation

To evaluate the differences between these approaches, we generate random task sets where the low-criticality tasks are of one of the three different types, and compare their EDF-schedulability according to the analysis presented in this paper. First, we define a few constants used for the task set generation, namely

$$\begin{aligned} \begin{array}{lr} Pr_\textsc {hi} = 0.5, &{} \quad { the\,probability\,of\,each\,task\,to\,be\,of\,high\,criticality,}\\ e^\textsc {lo} _\mathrm {max}= 10, &{} \quad { the\,maximum\,execution\,time\,budget\,in\,mode\,\textsc {lo},}\\ p^\textsc {lo} _\mathrm {max}= 200, &{} \quad { the\,maximum\,period\,in\,mode\,\textsc {lo},}\\ e^\textsc {hi} _\mathrm {fact}= 4, &{} \quad { the\,maximum\,factor\,of\,execution\,time\,increase\,in\,\textsc {hi} \,(for\,\textsc {hi} {\hbox {-}}tasks),}\\ e^\textsc {lo} _\mathrm {fact}= 0.5, &{} \quad { the\,minimum\,factor\,of\,execution\,time\,decrease\,in\,\textsc {hi} \,(for\,\textsc {lo} {\hbox {-}}tasks),}\\ p^\textsc {lo} _\mathrm {fact}= 2, &{} \quad { the\,maximum\,factor\,of\,period\,increase\,in\,\textsc {hi} \,(for\,\textsc {lo} {\hbox {-}}tasks).} \end{array} \end{aligned}$$

The first three constants were chosen somewhat arbitrarily. The value for $e^\textsc {hi} _\mathrm {fact}$ was set to $4$ because a difference of up to four times between, say, measurement-based and static analysis-based WCET estimates seems fairly realistic for complex code and hardware platforms. To balance this, low-criticality tasks may be limited to as little as half their ordinary execution time ($e^\textsc {lo} _\mathrm {fact}$) and double their periods ($p^\textsc {lo} _\mathrm {fact}$) in the high-criticality mode.

Each task set is generated with a target utilization $U^*$ in mind. A generated task set $T$ is considered valid only if $U_\mathrm {avg}(T) \in [U^*- 0.005,\, U^*+ 0.005]$, where

$$\begin{aligned} U_\mathrm {avg}(T) \;\mathop {=}\limits ^{\tiny def }\; \sum _{\mu _{i} \in M(T)} \frac{U(T, \mu _{i})}{|M(T)|} \end{aligned}$$

is the average utilization of $T$ and $U(T, \mu _{i})$ is the asymptotic utilization of $T$ in mode $\mu _{i}$. In addition, a task set $T$ is considered valid only if its utilization is at most $0.99$ in each mode, and each mode is EDF-schedulable in its steady-state. The former is a practical restriction to limit analysis time, the latter a restriction to the interesting cases where task sets are not trivially unschedulable no matter how the mode changes are handled. Generated task sets that are deemed invalid are simply discarded and new ones are generated instead. The task sets are always generated three at a time, each with low-criticality tasks of a certain type, the parameters of the tasks in each of the sets are kept identical where applicable. The details of the task set generation are found in Algorithm 1. Note that the values of the $\delta$-labels for the tasks of type lo-delay-QoS are not determined by Algorithm 1, we will instead search for suitable values as part of the experiment. Also note that task sets with type lo-no-QoS tasks can have smaller average utilization than the other two task sets, $U^*$ is only compared against the average utilization of the task sets with QoS tasks.

1.3 Evaluation

When determining the EDF-schedulability of the task sets, we use the deadline tuning algorithm TuneSystem from Ekberg and Yi (2014). It is directly applicable to the task sets with low-criticality tasks of type lo-no-QoS and lo-basic-QoS (indeed, even the schedulability analysis in Ekberg and Yi (2014) is equivalent to the one in this paper for such tasks). For task sets with type lo-delay-QoS tasks, we use the naive extension of TuneSystem that only attempts to tune deadlines of high-criticality tasks.

We still have to determine the values of the $\delta$ parameters of the tasks of type lo-delay-QoS. For simplicity, we assume that all such tasks in a task set $T_\mathrm {delay}$ have the same value for their $\delta$ parameter. For each such task set we do a binary search on the ordered set $\left\{ 0, \ldots , p^\textsc {lo} _\mathrm {max}\right\}$ to find the minimal value for $\delta$ with which $T_\mathrm {delay}$ is deemed EDF-schedulable. Figure 11 shows the acceptance ratios of the various types of task sets, without QoS, with basic QoS and with delayed QoS. For the task sets with delayed QoS, acceptance ratios are plotted for when the $\delta$ parameters are bounded by some different constants. Each data point is based on 10,000 randomly generated task sets.

Fig. 11

Acceptance ratios for the three different types of task sets

From Fig. 11 we can see that even for relatively small delays, less than half of the maximum period, acceptance ratios are practically the same for task sets with QoS as for those without. In contrast, task sets with basic QoS that use the same mode-switching logic for both high- and low-criticality tasks have significantly lower acceptance ratios. Even when $\delta = 0$ there was an increase in acceptance ratio compared to the basic QoS. The reason is that it is easier to schedule tasks that drop active jobs at a mode switch and immediately release new ones than it is to schedule tasks with carry-over jobs.

Figure 12 shows the average value for the $\delta$ parameter that was necessary to make the task sets $T_\mathrm {delay}$ schedulable, when such a value could be found in $\left\{ 0, \ldots , p^\textsc {lo} _\mathrm {max}\right\}$. The error bars indicate the standard deviation of the sample. It is clear from the figure that even for very large utilizations, small $\delta$ parameters tend to be sufficient.

Fig. 12

The average of the minimum values for $\delta$ needed to make the task sets schedulable

Appendix 2: A larger system example

Burns (2014) recently attempted to unify various notions of mode changes that has been used in the literature, in particular various general mode changes and criticality mode changes. He provides a high-level description of an example cruise-control system in a car that is complicated by having, at the same time, different types of modes and mode change protocols. As another motivation for MS-DRT, we outline in this section how it can be used to model that example system. First, we briefly summarize the terminology of Burns (2014), starting with the three main types of modes that he identifies.

• Normal functional modes are modes that are switched between as part of the regular operation of the system.

• Exceptional functional modes are modes that are entered as a response to some rare events.

• Degraded functional modes are modes entered as a consequence of some error or fault in the system, where some normal functionalities may be shed in order to give priority to safety-critical functions.

Further, Burns characterizes three main types of mode changes:

• Immediate mode changes cause old jobs to be suspended or aborted, and new jobs from the new mode to be started immediately.

• Bounded mode changes wait until there are no active jobs from the old mode and then switch cleanly to the new mode.

• Phased mode changes let old jobs finish, and new jobs may be released within some bounded time, even if all old jobs have not finished.

Transitions for the above three types of mode changes can be modeled with MS-DRT, for example as in Fig. 13. Note that transitions for immediate and bounded mode changes are modeled in the same way, but with different interpretations of the semantics. For immediate transitions, we interpret the mode switch event as being propagated immediately, causing any active job to be dropped (by setting its execution time budget to 0 in vertex $v$) and a new job to be released immediately at $w$. On the other hand, for bounded transitions we interpret the mode switch event to occur when all old jobs have finished, at which point no job from $u$ is dropped at the transition to $v$. For the schedulability analysis, these two scenarios look identical. In a phased transition, old active jobs are brought along to the new mode (though we allow changing their parameters in the process), and new jobs may be released before all of them are finished.

Fig. 13

Simple modeling of transitions for different mode change types

The cruise-control system described by Burns consists of two normal functional modes, standby (sb) and speed control (sc), and one exceptional mode, collision avoidance (ca). According to Burns, transitions between sb and sc should be either bounded or phased, and transitions from either of them to ca should be immediate. We pick phased transitions between sb and sc to make the example more interesting.

In addition, the system software is partitioned into two criticality levels, called SIL2 and SIL4. Code for SIL4 has two WCET estimates, one lower measurement-based estimate that is valid at SIL2 and one higher static-analysis based valid at SIL4. If at any time some WCET estimate at SIL2 turns out to be invalid, the system should enter some form of degraded mode where more time is given to the most critical tasks at the expense of the less critical. For the critical tasks, this would imply some kind of phased transition where execution-time budgets of active jobs get immediately inflated. In effect, we get six modes in total, the three modes sb, sc and ca using SIL2 WCET assumptions, and degraded versions of the same modes valid at SIL4. We call the modes $\mathrm {\textsc {sb}}_2$, $\mathrm {\textsc {sc}}_2$ and $\mathrm {\textsc {ca}}_2$ in SIL2, and $\mathrm {\textsc {sb}}_4$, $\mathrm {\textsc {sc}}_4$ and $\mathrm {\textsc {ca}}_4$ in SIL4. With these names we can form the mode structure of the system as in Fig. 14.

Fig. 14

Mode structure of the cruise-control system

Recall that MS-DRT does not impose any minimum separation delays between mode switches, other than what is explicitly put into the tasks themselves. This means that the schedulability analysis described earlier is valid for all possible sequences of mode switches, including complex situations such as a transition to $\mathrm {\textsc {ca}}_2$ happening in the middle of a phased transition between $\mathrm {\textsc {sb}}_2$ and $\mathrm {\textsc {sc}}_2$, closely followed by a transition to $\mathrm {\textsc {ca}}_4$. This was identified by Burns as a difficult problem.

In the system description given for this example, one particular task was also outlined. This is a sporadic task responsible for proximity analysis. It is stated that it should run in all three modes, but have a smaller period in ca. We assume that it is meant to have the same parameters in both sb and sc. Additionally, we assume that it belongs to the higher criticality level (SIL4), and therefore should run also in the degraded modes with a larger execution time budget. In Fig. 15 we have modeled this task. As no parameter values were given by Burns, we have arbitrarily picked some. We picked a WCET of 4 time units at SIL2 and 7 time units at SIL4. For the period we chose 50 time units in the various sb and sc modes, and 30 time units in the ca modes. The delay associated with the phased transition between sb and sc is set to 100. All deadlines are implicit.

Fig. 15

The proximity analysis task

This particular task was easy to model with only two vertices per mode. One work vertex per mode, with the name of the mode superscripted by “w”, captures the sporadic behavior of the task in that mode. Another gate vertex, superscripted instead by “g”, captures mode transition logic between modes at either SIL2 or SIL4 in the manner showed in Fig. 13. When switching from some mode at SIL2 to the corresponding one at SIL4 (e.g., from $\mathrm {\textsc {sb}}_2$ to $\mathrm {\textsc {sb}}_4$) the mode switching logic is that control is just moved to a mirrored version of the same vertex in the higher criticality level. We have intentionally omitted a mode switching edge from $\mathrm {\textsc {ca}}_2^\mathrm {g}$ to $\mathrm {\textsc {ca}}_4^\mathrm {g}$ with the interpretation that no time ever passes before moving on from $\mathrm {\textsc {ca}}_2^\mathrm {g}$ to $\mathrm {\textsc {ca}}_2^\mathrm {w}$.

In Burns’ description, there is no mention of mode changes being possible in order to go back from a ca mode to a sb or sc mode, but this seems like a desirable feature and may have been unintentionally omitted from the description. Adding this feature to a task such as the one in Fig. 15 is not difficult. Additionally, it would be possible to model mode switches from a SIL4 mode back to the corresponding SIL2 mode, resulting in the strongly connected mode structure in Fig. 16. The easiest way to model this would be with bounded transitions and the interpretation that such a mode switch can happen at any idle time, but it is also possible to model something more elaborate, e.g., as in Example 2.

Fig. 16

An extended mode structure that is strongly connected

We note that the task in Fig. 15 is quite large. Manually crafting such tasks certainly puts a burden on the system designer and would likely be error-prone. We envision that large tasks in practice should be synthesized by some model-based design tool or, at least, be manually modeled using some higher-level representation with syntactic sugar for common constructs.

Appendix 3: Proof of Lemma 3

To prove Lemma 3, we first define a relation on demand pairs and prove an auxiliary lemma.

Definition 5

(Cover relation) A demand pair $\langle e, d \rangle$ covers another demand pair $\langle e', d' \rangle$, denoted , if and only if

$$\begin{aligned} e \geqslant e' \;\text { and }\; e - e' \geqslant d - d'. \end{aligned}$$

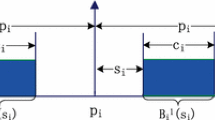
Figure 17 illustrates the cover relation. The intuition behind the cover relation is that a demand pair should cover all other demand pairs that are no more problematic from a scheduling point of view.

Fig. 17

The demand pair $(3, 5)$ covers all pairs in the shaded area

The subset of demand pairs used to define $\mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}^{\,\star }(\tau _{}, \ell )$ covers the set of demand pairs used to define $\mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}^\mathrm {\,ub}(\tau _{}, \ell )$, as shown in the following lemma.

Lemma 5

For each demand pair $\langle e, d \rangle \in \mathrm {nco}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{}) \,\bigcup \, \mathrm {co}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$ there exist an $\langle e^\star , d^\star \rangle \in \mathrm {nco}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{}) \,\bigcup \, \mathrm {co}^{\star }_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$ such that .

Proof

The lemma trivially holds for each $\langle e, d \rangle \in \mathrm {nco}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$ because the cover relation is reflexive.

We consider instead a demand pair $\langle e, d \rangle \in \mathrm {co}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$. From Eq. (11) it is evident that $\langle e, d \rangle = \mathrm {pair}_\mathrm {co}(u, \pi , x)$ for some $(u, \pi , x) \in \mathrm {Vals}$. We split the proof into three cases.

Case 1 ($x \geqslant e(u)$):

Let $\langle e^\star , d^\star \rangle = \mathrm {pair}_\mathrm {co}(u, \pi , e(u))$. Clearly, $\langle e^\star , d^\star \rangle \in \mathrm {co}^{\star }_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$. We calculate

$$\begin{aligned} e&= \tilde{e}_\mathrm {co}(u, \pi , x)\\&= e_\mathrm {co}(u, \pi _{1}, x) + \tilde{e}(\pi _{2 \cdots |\pi |})\\&= e_\mathrm {co}(u, \pi _{1}, e(u)) + \tilde{e}(\pi _{2 \cdots |\pi |})\\&= \tilde{e}_\mathrm {co}(u, \pi , e(u))\\&= e^\star \end{aligned}$$

and $d = \tilde{d}_\mathrm {co}(u, \pi , x) \geqslant \tilde{d}_\mathrm {co}(u, \pi , e(u)) = d^\star$. It follows that .

Case 2 ($x \leqslant e(u) - e(\pi _{1})$):

Let $\langle e^\star , d^\star \rangle = \mathrm {pair}_\mathrm {nco}(\pi _{2 \cdots |\pi |})$. Because either $|\pi _{2 \cdots |\pi |}| = 0$ or $\pi _{2} \in \mathrm {first}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$, we have $\langle e^\star , d^\star \rangle \in \mathrm {nco}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$. Further,

$$\begin{aligned} e&= \tilde{e}_\mathrm {co}(u, \pi , x)\\&= e_\mathrm {co}(u, \pi _{1}, x) + \tilde{e}(\pi _{2 \cdots |\pi |})\\&= 0 + \tilde{e}(\pi _{2 \cdots |\pi |})\\&= e^\star \end{aligned}$$

and $d = \tilde{d}_\mathrm {co}(u, \pi , x) \geqslant \tilde{d}(\pi _{2 \cdots |\pi |}) = d^\star$. It follows that .

Case 3 ($e(u) - e(\pi _{1}) < x < e(u)$):

Again, let $\langle e^\star , d^\star \rangle = \mathrm {pair}_\mathrm {co}(u, \pi , e(u))$. Now,

$$\begin{aligned} e&= \tilde{e}_\mathrm {co}(u, \pi , x)\\&= e_\mathrm {co}(u, \pi _{1}, x) + \tilde{e}(\pi _{2 \cdots |\pi |})\\&= e_\mathrm {co}(u, \pi _{1}, e(u)) - e(u) + x + \tilde{e}(\pi _{2 \cdots |\pi |})\\&= \tilde{e}_\mathrm {co}(u, \pi , e(u)) - e(u) + x\\&= e^\star - e(u) + x. \end{aligned}$$

Similarly,

$$\begin{aligned} d&= \tilde{d}_\mathrm {co}(u, \pi , x)\\&\geqslant \tilde{d}_\mathrm {co}(u, \pi , e(u)) - e(u) + x\\&= d^\star - e(u) + x. \end{aligned}$$

It follows that $e^\star \geqslant e$ and $e^\star - e = e(u) - x \geqslant d^\star - d$, and therefore that . $\square$

We can now prove Lemma 3.

Proof of Lemma 3  From Eqs. (12) and (14) we know that $\mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}^{\,\star }(\tau _{}, \ell )$ is defined by a subset of the set of demand pairs defining $\mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}^\mathrm {\,ub}(\tau _{}, \ell )$. It follows directly that $\mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}^{\,\star }(\tau _{}, \ell ) \leqslant \mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}^\mathrm {\,ub}(\tau _{}, \ell )$, and the $\Longleftarrow$ direction of the lemma holds.

We instead consider the $\Longrightarrow$ direction. From Eq. (12) it is clear that if there exists an $\ell _1 \geqslant 0$ such that $\sum _{\tau _{} \in T}{\mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}^\mathrm {\,ub}(\tau _{}, \ell _1)} > \ell _1$, then for each $\tau _{} \in T$ there must exist demand pairs $\langle e_{\tau _{}}, d_{\tau _{}} \rangle \in \mathrm {nco}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{}) \,\bigcup \, \mathrm {co}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$ such that

$$\begin{aligned} \sum _{\tau _{} \in T}{e_{\tau _{}}} > \ell _1 \quad \text {and}\quad \max _{\tau _{} \in T{}}(d_{\tau _{}}) \leqslant \ell _1. \end{aligned}$$

(17)

From Lemma 5 we know that for each of the demand pairs $\langle e_{\tau _{}}, d_{\tau _{}} \rangle$ there exists some demand pair $\langle e^\star _{\tau _{}}, d^\star _{\tau _{}} \rangle \in \mathrm {nco}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{}) \,\bigcup \, \mathrm {co}^{\star }_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$ such that . By Definition 5 we have

$$\begin{aligned} \sum _{\tau _{} \in T}{e^\star _{\tau _{}}} - \sum _{\tau _{} \in T}{e_{\tau _{}}} \;\geqslant \; \max _{\tau _{} \in T}(d^\star _{\tau _{}}) - \max _{\tau _{} \in T}(d_{\tau _{}}). \end{aligned}$$

(18)

From Eqs. (17) and (18) it follows that

$$\begin{aligned} \sum _{\tau _{} \in T}{e^\star _{\tau _{}}} \;>\; \max _{\tau _{} \in T}(d^\star _{\tau _{}}). \end{aligned}$$

(19)

Let $\ell _2 = \max _{\tau _{} \in T}(d^\star _{\tau _{}})$. From the existence of the demand pairs $\langle e^\star _{\tau _{}}, d^\star _{\tau _{}} \rangle$ and Eqs. (14) and (19) we know that

$$\begin{aligned} \sum _{\tau _{} \in T}{\mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}^{\,\star }(\tau _{}, \ell _2)} \;\geqslant \; \sum _{\tau _{} \in T}{e^\star _{\tau _{}}} \;>\; \ell _2. \square \end{aligned}$$

Appendix 4: Table of notations used for the analysis

$\tau _{} \in T$	An MS-DRT task $\tau _{}$ in task set $T$
$\mu _{i} \in M(T)$	A mode $\mu _{i}$ in the set of modes of $T$
$V(\tau _{})$	Job types (vertices) of task $\tau _{}$
$E_\mathrm {cf}(\tau _{})$	Control-flow edges of task $\tau _{}$
$E_\mathrm {ms}(\tau _{})$	Mode-switch edges of task $\tau _{}$
$e(v), d(v), \mathrm {\mu }(v)$	Execution time, relative deadline and mode of job type $v$
$G(T)$	Mode structure of task set $T$
$\mathrm {pred}_{G(T)}(\mu _{i})$	Modes that can precede $\mu _{i}$ in $G(T)$
$\mathrm {\textsc {drt}}_{\mu _{i}}(\tau _{})$	The subgraph in $(V(\tau _{}), E_\mathrm {cf}(\tau _{}))$ corresponding to mode $\mu _{i}$
$\varPi _{\mu _{i}}(\tau _{})$	Set of finite paths through $\mathrm {\textsc {drt}}_{\mu _{i}}(\tau _{})$
$\pi _{n}$	The $n$th vertex on path $\pi$
$|\pi |$	Length (in number of vertices) of path $\pi$
$\pi _{n \cdots m}$	Subpath of $\pi$ between the $n$th and $m$th vertices (inclusive)
$\tilde{e}(\pi )$	Cumulative execution time of job types on path $\pi$
$\tilde{d}(\pi )$	Smallest interval size that fits jobs from all vertices on path $\pi$
$E_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$	Mode-switch edges from $\mu _{j}$ to $\mu _{i}$ in task $\tau _{}$
$\mathrm {first}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$	Vertices in $V(\tau _{})$ that can directly follow a switch from $\mu _{j}$ to $\mu _{i}$
$e_\mathrm {co}(u, v, x)$	Max execution left of carry-over job at $(u, v) \in E_\mathrm {ms}(\tau _{})$, given $x$
$d_\mathrm {co}(u, v, x)$	Remaining scheduling window size of carry-over job, given $x$
$p_\mathrm {co}(u, v, w, x)$	Min delay from mode switch to edge $(v, w) \in E_\mathrm {cf}(\tau _{})$, given $x$
$\tilde{e}_\mathrm {co}(u, \pi , x)$	As $e_\mathrm {co}(u, v, x)$, generalized to path $\pi$
$\tilde{d}_\mathrm {co}(u, \pi , x)$	As $d_\mathrm {co}(u, v, x)$, generalized to path $\pi$
$\mathrm {nco}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$	Set of demand pairs for paths not starting with a carry-over job
$\mathrm {co}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$	Set of demand pairs for paths starting with a carry-over job
$\mathrm {co}^{\star }_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$	Subset of $\mathrm {co}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$ of “critical” demand pairs
$\mathrm {idbf}_{\mu _{i}}(T, \ell )$	Exact internal demand bound function of $T$
$\mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}(T, \ell )$	Exact transitional demand bound function of $T$
$\mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}^\mathrm {\,ub}(\tau _{}, \ell )$	Over-approximate transitional demand bound function of $\tau _{}$
$\mathrm {idbf}^{\,\star }_{\mu _{i}}(\tau _{}, \ell )$	Exact internal demand bound function of $\tau _{}$
$\mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}^{\,\star }(\tau _{}, \ell )$	Simplified version of $\mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}^\mathrm {\,ub}(\tau _{}, \ell )$, preserving schedulability
$\mathrm {\textsc {drt}}_{\mu _{j} \rightarrow \mu _{i}}(\tau _{})$	DRT task with demand bound function equal to $\mathrm {tdbf}_{\mu _{j} \rightarrow \mu _{i}}^{\,\star }(\tau _{}, \ell )$
$\mathcal {S}_{\mathrm {\textsc {edf}}}(T,\, {\mu _{i}})$	Internal schedulability of $T$ in $\mu _{i}$, equivalent to $\mathcal {S}^{\star }_\mathrm {\textsc {edf}}(T,\, {\mu _{i}})$
$\mathcal {S}_\mathrm {\textsc {edf}}(T,\, {\mu _{j} \rightarrow \mu _{i}})$	Transitional schedulability of $\mu _{i}$ when reached from $\mu _{j}$
$\mathcal {S}^{\star }_\mathrm {\textsc {edf}}(T,\, {\mu _{j} \rightarrow \mu _{i}})$	Implies $\mathcal {S}_\mathrm {\textsc {edf}}(T,\, {\mu _{j} \rightarrow \mu _{i}})$ when $\mu _{j}$ is schedulable