User’s mobility effect on the performance of wireless cellular networks serving elastic traffic

Abstract

The objective of the present paper is to give an analytic approximation of the performance of elastic traffic in wireless cellular networks accounting for user’s mobility. To do so we build a Markovian model for users arrivals, departures and mobility in such networks; which we call WET model. We firstly consider intracell mobility where each user is confined to remain within its serving cell. Then we consider the complete mobility where users may either move within each cell or make a handover (i.e. change to another cell). We propose to approximate the WET model by a Whittle one for which the performance is expressed analytically. We validate the approximation by simulating an OFDMA cellular network. We observe that the Whittle approximation underestimates the throughput per user of the WET model. Thus it may be used for a conservative dimensioning of the cellular networks. Moreover, when the traffic demand and the user speed are moderate, the Whittle approximation is good and thus leads to a precise dimensioning.

Appendix 1: Completely aimless mobility

We present in this appendix 1 mobility model based on the following assumptions (see [29]):

• The speeds of the users are considered as random vectors in ${\mathbb{R}}^{2}$ and are assumed independent and identically distributed.

• The speed direction of a typical user is a random variable which is uniformly distributed in [0,2π].

Following the authors of [23] we call this model completely aimless mobility.

Let V be the speed magnitude of a typical user, F be its cumulative distribution function and υ = E[V] be its mean.

1.1 1.1 Sojourn duration

We are interested in the user’s sojourn duration in a given geographic zone of area A and perimeter L. Much as in [29], we derive a relation between the average sojourn duration (which will be useful in the construction the mobility kernel in the following section) and the average speed.

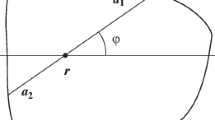
We are interested in the users crossing an infinitesimal element dl of the border (for example from outside to inside) within an infinitesimal duration dt. Such users are located in a rectangle of sides dl and Vcosαdt, as illustrated in Fig. 5, where:

• V is the user’s speed magnitude;

• and α is the angle formed by the user’s speed vector and the perpendicular to dl.

Fig. 5

Rectangle containing customers crossing an element dl of the border during dt

Integrating over V and α, we obtain the average number of users crossing an element dl of the border of the zone, from outside to inside, during dt

$$ \int\limits_{-\pi/2}^{\pi/2}\int\limits_{0}^{+\infty}VF\left( dV\right) \cos\alpha \frac{d\alpha}{2\pi}\rho dldt=\frac{\upsilon\rho} {\pi}dldt $$

where ρ is the density of users per surface unit, F is the cumulative distribution function of the user’s speed magnitude and υ = E[V]. Then the average number of users crossing the zone border per time-unit denoted λ (which is the average arrival rate of users to the zone) is given by

$$ \lambda=\upsilon\rho L/\pi $$

(14)

where L is the perimeter of the zone.

Denote τ the average sojourn duration of a user in a zone and $\bar{M}$ the average number of users in the zone. By Little’s formula, we have

$$ \bar{M}=\lambda\tau $$

which gives

$$ \tau=\bar{M}\lambda^{-1}=\rho A\frac{\pi}{\upsilon\rho L}= \frac{\pi}{\upsilon}\frac{A}{L} $$

(15)

where A is the surface of the zone. For a disc of radius R, we have A/L = R/2.

The authors of [23] consider an exponential distribution for the sojourn duration. This assumption is justified by [19].

1.2 1.2 Intracell mobility

The cell is modeled by a disc of radius R which is divided into J rings. Each ring denoted by some j ∈ {1, …, J} is delimited by discs with radii r _j-1 and r _j where r ₀ = 0 and r _J  = R. Let A _j  = π(r ² _j  − r ²_j-1 ) be the surface of ring j. Of course J should be large enough to capture correctly the geometry of the problem.

Consider the case where mobility is within a given cell. Denote λ ^′ _j the inverse of the average sojourn duration of users at ring j. Applying (15) gives

$$ \begin{aligned} \lambda_{j}^{\prime}&=\frac{\upsilon}{\pi}\frac{L_{j}}{A_{j}}= 2\upsilon\frac{r_{j}+r_{j-1}}{A_{j}},\quad j=1,\ldots,J-1\\ \lambda_{J}^{\prime}&=\frac{\upsilon}{\pi}\frac{L_{J}} {A_{J}}=2\upsilon \frac{r_{J-1}}{A_{J}} \end{aligned} $$

A user finishing its sojourn at ring j is routed:

• either to ring j − 1 or to ring j + 1 with respective probabilities p ^′_j,j−1  = r _j-1/(r _j  + r _j−1) and p ^′_j,j+1  = r _j /(r _j  + r _j−1), if j = 2, …, J − 1;

• to ring 2 with probability 1, if j = 1;

• to ring J − 1 with probability 1, if j = J.

Define the mobility kernel (λ _jk ) on {1, …, J} by

$$ \lambda_{jk}=\lambda_{j}^{\prime}p_{jk}^{\prime},\quad j,k\in\left\{1,\ldots,J\right\} . $$

We deduce from the above results that

$$ \begin{aligned} \lambda_{j,j-1}&=2\upsilon\frac{r_{j-1}}{A_{j}},\quad j=2,\ldots,J\\ \lambda_{j,j+1}&=2\upsilon\frac{r_{j}}{A_{j}},\quad j=1,\ldots,J-1. \end{aligned} $$

(16)

Proposition 6

The mobility kernel (λ _{;j, k ∈jk} {1, ..., J}) where the λ _jk are given by (16) admits

$$ \sigma_{j}=\frac{A_{j}}{\pi R^{2}},\quad j=1,\ldots,J $$

(17)

as invariant probability measure, i.e. (σ _j , j ∈ {1, …, J}) is solution of the following balance equations

$$ \sigma_{j}\sum_{k}\lambda_{j,k}=\sum_{k}\sigma_{k}\lambda_{k,j},\quad j\in\left\{1,\ldots,J\right\} . $$

(18)

Proof

Equation (18) may be written as follows

$$ \left\{\begin{array}{ll} \sigma_{j}\left( \lambda_{j,j-1}+\lambda_{j,j+1}\right) =\sigma_{j-1} \lambda_{j-1,j}+\sigma_{j+1}\lambda_{j+1,j} & \quad\hbox {for } j=2,\ldots,J-1\\ \sigma_{1}\lambda_{1,2}=\sigma_{2}\lambda_{2,1} & \\ \sigma_{J}\lambda_{J,J-1}=\sigma_{J-1}\lambda_{J-1,J} &\\ \end{array}\right. $$

For the rates (16) we get

$$ \left\{ \begin{array}{ll} \sigma_{j}\frac{r_{j}+r_{j-1}}{A_{j}}=\sigma_{j-1}\frac{r_{j-1}}{A_{j-1} }+\sigma_{j+1}\frac{r_{j}}{A_{j+1}} & \quad\hbox {for }j=2,\ldots,J-1\\ \sigma_{1}\frac{r_{1}}{A_{1}}=\sigma_{2}\frac{r_{1}}{A_{2}} & \\ \sigma_{J}\frac{r_{J}-1}{A_{J}}=\sigma_{J-1}\frac{r_{J-1}}{A_{J-1}} &\\ \end{array} \right. $$

which clearly admits σ given by (17) as solution.□

We introduce a “ virtual” state 0 which can be seen as a location outside the cell, and which represents the location of calls arriving to or leaving the cell. We consider now some arrival rates denoted λ_0j and some departure rates denoted λ_j0. We call (λ _jk ;j, k ∈ {0, 1, …, J}) the traffic kernel; which may be seen as an extension of the mobility kernel (λ _jk ;j, k ∈ {1, …, J}) to {0, 1, …, J}.

Proposition 7

Consider the motion rates (16), and let λ_0j  > 0 and λ_j0 > 0 be the arrival and departure rates respectively. Then for each speed υ ≥ 0, the following traffic equations

$$ \rho_{0}=1 \hbox { and }\rho_{j}\sum_{k=0}^{J}\lambda_{jk}=\sum_{k=0}^{J} \rho_{k}\lambda_{kj},\quad j\in\left\{ 1,\ldots,J\right\} $$

(19)

(associated to the traffic kernel ( _jk ;j, k ∈ {0, 1, …, J})) admit a unique solution.□

Proof

The traffic kernel (λ _jk ;j, k ∈ {0, 1, …, J} ) is irreducible by the positivity of the arrival and departure rates. Since the state space {0, 1, …, J} is finite, the Markov process associated to the traffic kernel is positive recurrent and admits an invariant measure ρ with positive terms and unique up to a multiplicative factor (see [18]). Hence (19) admit a unique solution.

1.3 1.3 Intercell mobility

Let λ ^′ _u be the inverse of the average sojourn duration of users within cell u. Applying (15) we get

$$ \lambda_{u}^{\prime}=\frac{\upsilon}{\pi}\frac{L}{A}=\frac{2\upsilon} {\pi R} $$

(20)

where the perimeter equals L = 2πR and the area equals A = π R ². If each base station has six neighbors as in the toric hexagonal model, then a user finishing its sojourn in cell u is routed to a neighboring cell v with probability

$$ p_{u,v}^{\prime}=\frac{1}{6}. $$

Define the mobility kernel λ_u,v on the set of cells by

$$ \begin{aligned} \lambda_{u,v} &=\lambda_{u}^{\prime}p_{u,v}^{\prime}\\ &=\frac{1}{6}\lambda_{u}^{\prime}=\frac{\upsilon}{3\pi R} \end{aligned} $$

(21)

for each pair of neighboring cells u, v.

1.4 1.4 Complete mobility

Consider now a network of hexagonal cells such that each one has exactly six neighbors. Each cell is approximated by a disc and divided into J rings. The cells are indexed by $u\in{\mathcal{U}}=\left\{1,\ldots,U\right\}$, and the rings by $j\in{\mathcal{J}}=\left\{1,\ldots,J\right\}$. The ring j of the cell u is indexed by $uj\in{\mathcal{U}}\times{\mathcal{J}}$.

Remark 3

We may alternatively index the rings of cell u by (u − 1) J + 1, …(u − 1) J + J. Hence each ring is identified by some location x = {1, …, U × J}. From a given such location x, we may retrieve the index of the corresponding cell u and ring j by the Euclidean division

$$ x-1=\left(u-1\right) J+\left( j-1\right) ,\quad1\leq j\leq J. $$

Denote λ ^′ _uj the inverse of the average sojourn duration of users in the ring uj. Applying (15) gives

$$ \lambda_{uj}^{\prime}=\frac{\upsilon}{\pi}\frac{L_{j}} {A_{j}}=2\upsilon \frac{r_{j}+r_{j-1}}{A_{j}},\quad u\in{\mathcal{U}},j\in{\mathcal{J}}. $$

A user finishing its sojourn in ring uj is routed:

• to either ring u(j − 1) or ring u(j + 1) with respective probabilities p ^′_{uj,u(j – 1)}  = r _j−1/(r _j  + r _j−1) and p ^′_{uj,u(j + 1)}  = r _j /(r _j  + r _j−1), if j = 2, …, J − 1;

• to ring u2 with probability 1, if j = 1;

• to either ring u(J − 1) or ring vJ, where v is a neighbor of u, with respective probabilities p ^′_{uJ,u(J – 1)}  = r _J – 1/(r _J  + r _J – 1) and $p_{uJ,vJ}^{\prime}=\frac{1}{6}r_{J}/\left( r_{J}+r_{J-1}\right)$, if j = J.

Define the mobility kernel (λ_uj,vk) on ${\mathcal{U}}\times{\mathcal{J}}$ by

$$ \lambda_{uj,vk}=\lambda_{uj}^{\prime}p_{uj,vk}^{\prime},\quad u,v\in {\mathcal{U}},j,k\in{\mathcal{J}}. $$

We deduce from the above results that

$$ \left\{\begin{array}{ll} \lambda_{uj,u\left( j-1\right)}=2\upsilon\frac{r_{j-1}} {A_{j}}, & \quad j=2,\ldots,J\\ \lambda_{uj,u\left( j+1\right) }=2\upsilon\frac{r_{j}}{A_{j}}, & \quad j=1,\ldots,J-1\\ \lambda_{uJ,vJ}=\frac{1}{3}\upsilon\frac{r_{J}}{A_{J}}, & \quad v\hbox {\ is a neighbor of }u. \end{array} \right. $$

(22)

The result of Proposition 6 may be easily extended to the complete mobility case as follows.

Proposition 8

The mobility kernel $\left( \lambda_{uj,vk};uj,u,v\in{\mathcal{U}},j,k\in{\mathcal{J}}\right)$ given by ( 22 ) admits

$$ \sigma_{uj}=\sigma_{j}=\frac{A_{j}}{\pi R^{2}},\quad u\in{\mathcal{U}} ,j\in{\mathcal{J}} $$

as invariant probability measure, i.e. $\left( \sigma_{uj},u\in {\mathcal{U}},j\in{\mathcal{J}}\right)$ is solution of the following balance equations

$$ \sigma_{uj}\sum_{v\in{\mathcal{U}},k\in{\mathcal{J}}}\lambda_{uj,vk}=\sum _{v\in{\mathcal{U}},k\in{\mathcal{J}}}\sigma_{vk}\lambda_{vk,uj},\quad u\in{\mathcal{U}},j\in{\mathcal{J}}. $$

Proof

Besides the proof of Proposition 6, it remains to show that

$$ \sigma_{J}\left[ \lambda_{uJ,u(J-1)}+\sum_{v}\lambda_{uJ,vJ}\right] =\sigma_{J-1}\lambda_{u(J-1),uJ}+\sigma_{J}\sum_{v}\lambda_{vJ,uJ} $$

which is equivalent to

$$ \sigma_{J}\lambda_{uJ,u(J-1)}=\sigma_{J-1}\lambda_{u\left( J-1\right) ,uJ} $$

which holds true.□

We introduce a “virtual” location 0 which can be seen as a location outside the cell, and which represents the location of calls arriving to or leaving the network. We consider now some arrival rates denotes λ_0,uj and departure rates denoted λ_uj,0. We call $(\lambda_{uj,vk};uj,vk\in\left({\mathcal{U}}\times{\mathcal{J}}\right) \cup\left\{0\right\} )$ the traffic kernel; which may be seen as an extension of the mobility kernel $\left( \lambda_{uj,vk};uj,vk\in {\mathcal{U}}\times{\mathcal{J}}\right)$ to $\left( {\mathcal{U}}\times {\mathcal{J}}\right) \cup\left\{ 0\right\}$.

The following proposition shows the relation between the invariant measures of the traffic kernels associated to intracell and complete mobility models respectively.

Proposition 9

Assume that the arrival and departure rates don’t depend on the particular cell but only on the ring in which they occur; i.e. λ_0,uj  = λ_0,j and λ_uj,0 = λ_j,0. If$\left( \rho_{j};j\in{\mathcal{J}}\cup\left\{ 0\right\} \right)$is solution of the traffic equations (19), then$\left( \rho_{uj};uj\in\left( {\mathcal{U}}\times{\mathcal{J}}\right) \cup\left\{ 0\right\} \right)$defined by

$$ \rho_{u0}=\rho_{0}=1,\quad\rho_{uj}=\rho_{j},\quad u\in{\mathcal{U}} ,j\in{\mathcal{J}} $$

(23)

is solution of the traffic equations associated to the traffic kernel$(\lambda_{uj,uk};uj,uk\in\left( {\mathcal{U}}\times{\mathcal{J}}\right) \cup\left\{ 0\right\} )$; i.e. ρ_u0 = 1 and for all $u\in {\mathcal{U}},j\in{\mathcal{J}}$

$$ \rho_{uj}\sum_{vk\in\left( {\mathcal{U}}\times{\mathcal{J}}\right) \cup\left\{ 0\right\}}\lambda_{uj,vk}=\sum_{vk\in\left( {\mathcal{U}}\times {\mathcal{J}}\right) \cup\left\{ 0\right\} }\rho_{vk}\lambda_{vk,uj}. $$

(24)

Proof

Assume that $\left( \rho_{j};j\in{\mathcal{J}}\cup\left\{ 0\right\} \right)$ is a solution of (19). Let’s verify that $\left( \rho_{uj};uj\in\left( {\mathcal{U}}\times{\mathcal{J}}\right) \cup\left\{ 0\right\} \right)$ defined by ((23) satisfy (24), i.e. for j = 2, …, J − 1

$$ \rho_{j}\left( \lambda_{uj,0}+\lambda_{uj,u\left( j-1\right) } +\lambda_{uj,u\left( j+1\right) }\right) =\rho_{0}\lambda_{0,uj}+\rho _{j-1}\lambda_{u\left( j-1\right) ,uj}+\rho_{j+1}\lambda_{u\left( j+1\right) ,uj} $$

and

$$ \begin{aligned} \rho_{1}\left( \lambda_{u1,0}+\lambda_{u1,u2}\right) &=\rho_{0}\lambda _{0,u1}+\rho_{2}\lambda_{u2,u1}\\ \rho_{J}\left[ \lambda_{uJ,0}+\lambda_{uJ,u(J-1)}+\sum_{v}\lambda _{uJ,vJ}\right] &=\rho_{0}\lambda_{0,uJ}+\rho_{J-1}\lambda_{u(J-1),uJ} +\sum_{v}\rho_{J}\lambda_{vJ,uJ} \end{aligned} $$

which are clearly satisfied since λ_uj,uk = λ _jk and ∑ _v λ_uJ,vJ = ∑ _v λ_vJ,uJ.□