Use of flip ambiguity probabilities in robust sensor network localization

Abstract

Collinear or near collinear placement of some sensors in a wireless sensor network causes the location estimates of nearby sensors to be sensitive to erroneous distance measurements which leads to large location estimation errors. These errors and the possible propagation of these errors to the entire network or a large portion of it, thereby causing larger estimation errors for some sensors’ locations, is a major problem in localization. This phenomenon is well described in rigid graph theory, using the notion of “flip ambiguity”. This paper considers arbitrary sensor neighborhoods of two dimensional sensor networks and formulates an analytical expression for the probability of occurrence of the flip ambiguity. Based on the derived probability expression, a methodology is proposed to make the localization algorithms robust by calculating such flip ambiguity probabilities and eliminating potentially poor location estimates as well as assigning confidence factors to the estimated locations to prevent them from ruining the subsequent localization steps. The efficiency of the proposed methodology is demonstrated via a set of simulations.

Appendices

A Calculation of $P(\zeta_{AB}\mid p(A),p(B),p(C),p(D))$

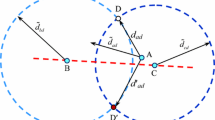
Denote by H _C the open half plane containing the sensor s _C , bordered by the line AB as shown in Fig. 11, then the complementary half plane on the other side of line AB can be denoted by $H_{\overline{C}}$. For a non-collinear neighborhood N _D  = {s _A , s _B , s _C }, H _C and $H_{\overline{C}}$ are well defined. Denote by p ^AB _C (D) and $p_{\overline{C}}^{AB}(D)$ the intersection points of the two circles ${{\mathcal{C}}(p(A),\overline{d}_{AD})}$ and ${{\mathcal{C}}(p(B),\overline{d}_{BD})}$. Without loss of generality, let $p_C^{AB}(D) \in H_C$, which will leave the other intersection point $p_{\overline{C}}^{AB}(D)\in H_{\overline{C}}$ as shown in Fig. 11.

Fig. 11

Division of the plane into two open halves H _C and $H_{\overline{C}}$ with respect to the three known neighbor locations p(A), p(B) and p(C)

When considering distance measurements from only two neighboring sensors s _A and s _B , both points p ^AB _C (D) and $p_{\overline{C}}^{AB}(D)$ are possible candidates for the location estimate $\hat{p}(D)$ of sensor s _D with $(\|p(A)-\hat{p}(D)\|-\overline{d}_{AD})^2+(\|p(B)-\hat{p}(D)\|-\overline{d}_{BD})^2=0$. When the third distance measurement from the neighboring sensor s _C is included in the localization process, a new candidate for the location estimate $\hat{p}(D)$ considering the third distance measurement $\overline{d}_{CD}$ is obtained as

$$ \begin{aligned} \hat{p}(D) \triangleq \arg \mathop{\hbox{min}}\limits_{\hat{p}^*(D)\in R_D^{AB}} J(\hat{p}^*(D)) \end{aligned} $$

(32)

where the cost function $J(\hat{p}^*(D))$ is defined as

$$ \begin{aligned} J(\hat{p}^*(D)) \triangleq& \left(\|p(A)-\hat{p}^*(D)\|-\overline{d}_{AD}\right)^2 \\ &\quad+\left(\|p(B)-\hat{p}^*(D)\|-\overline{d}_{BD}\right)^2 \\ &\quad+\left(\|p(C)-\hat{p}^*(D)\|-\overline{d}_{CD}\right)^2 \end{aligned} $$

(33)

Proposition A.1

With non-collinear neighbors s _A , s _B , s _C , the location estimate $\hat{p}(D)$ satisfies the following:

• i $\hat{p}(D) \in H_C \quad if\; 0\le\overline{d}_{CD}< \lambda_C-2\overline{\epsilon}$

• ii $\hat{p}(D) \in H_{\overline{C}} if\; \lambda_C+2\overline{\epsilon} <\overline{d}_{CD}\le R+\overline{\epsilon}$

where $\lambda_C=\frac{\|p(C)-p_C^{AB}(D)\|+\|p(C)-p_{\overline{C}}^{AB}(D) \|}{2}$.

Proof

Because of Assumption 2, we have (i) $D\in R_D^{AB}=R_{D_1}^{AB}\cup R_{D_2}^{AB}$ and (ii) D lies in the annulus with center C and radii $\overline{d}_{CD}\pm \overline{\epsilon}$. Denote the intersection regions of this annulus with R ^AB _D ∩ H _C and $R_D^{AB}\cap H_{\overline{C}}$ by S _{C_1} and $S_{\overline{C}_1}$ respectively; and the reflections of S _{C_1} and $S_{\overline{C}_1}$ with respect to AB by $S_{\overline{C}_2}$ and S _{C_2} respectively. Let S _C  = S _{C_1} ∪ S _{C_2} and $S_{\overline{C}}=S_{\overline{C}_1} \cup S_{\overline{C}_2}$. Note that $S_C \subset R_D^{AB} \cap H_C$ and $S_{\overline{C}} \subset R_D^{AB} \cap H_{\overline{C}}$ and that neither S _C nor $S_{\overline{C}}$ is empty set since each of them contains either D or the reflection of D with respect to AB. The value of $\hat{p}^*(D)$ minimizing (A.1) lies in either S _C or $S_{\overline{C}}$ since (i) at least one of the three quadratic components of $J(\hat{p}^*(D))$ is larger than $\overline{\epsilon}^2$ and hence $J(\hat{p}^*(D))>\overline{\epsilon}^2$ outside $S_C \cup S_{\overline{C}}$ and (ii) $S_C \cup S_{\overline{C}}$ contains points $\hat{p}^*(D)$ at which $J(\hat{p}^*(D))\le \overline{\epsilon}^2$ (the intersection points of the circles ${{\mathcal{C}}(A,\overline{d}_{AD}), {\mathcal{C}}(B,\overline{d}_{BD}), {\mathcal{C}}(C,\overline{d}_{CD})}$). □

First consider the case $0\le \overline{d}_{CD} < \lambda_C -2\overline{\epsilon}$. Noting that $\left\| p(C)-p_C^{AB}(D)\right\| < \lambda_C < \left\| p(C)-p_{\overline{C}}^{AB}(D) \right\|$ and analyzing all possible values of $\overline{d}_{CD} < \lambda_C - 2\overline{\epsilon}$, it can be established that

$$ \begin{aligned} \left\| \left\| p(C)-p_C^{AB}(D)\right\| - \overline{d}_{CD}\right\| < \left\|\left \| p(C)-p_{\overline{C}}^{AB}(D)\right\| - \overline{d}_{CD}\right\| -4\overline{\epsilon} \end{aligned} $$

(34)

For each point $\hat{p}^*(D)\in S_{\overline{C}}$, the reflection $\hat{p}_2^*(D)\in S_C$ of $\hat{p}^*(D)$ with respect to AB satisfies

$$ \begin{aligned} \| p(A) - \hat{p}^*(D) \| &= \| p(A) - \hat{p}_2^*(D) \| \\ \| p(B) - \hat{p}^*(D) \| &= \| p(B) - \hat{p}_2^*(D) \| \end{aligned} $$

Hence we have

$$ J(\hat{p}^*(D))-J(\hat{p}_2^*(D)) = (\| p(C)-\hat{p}^*(D)\|-\overline{d}_{CD})^2 - \left(\| p(C)-\hat{p}_2^*(D)\|-\overline{d}_{CD}\right)^2 $$

(35)

Furthermore, since $\hat{p}^*(D)\in S_{\overline{C}} \subset R_D^{AB} \cap H_{\overline{C}}$ and $\hat{p}_2^*(D)\in S_C \subset R_D^{AB} \cap H_C$, we have

$$ \begin{aligned} \| \| p(C) - \hat{p}^*(D) \| - \| p(C) - p_{\overline{C}}^{AB}(D) \| \| &\le 2\overline{\epsilon}\\ \| \| p(C) - \hat{p}_2^*(D) \| - \| p(C) - p_C^{AB}(D) \| \| &\le 2\overline{\epsilon} \end{aligned} $$

which, respectively imply

$$ \left\|\left \| p(C) - \hat{p}^*(D) \right\| - \overline{d}_{CD}\right\|\ge \left\| \left\| p(C) - p_{\overline{C}}^{AB}(D) \right\| - \overline{d}_{CD} \right\| - 2\overline{\epsilon} $$

(36)

$$ \| \| p(C) - \hat{p}_2^*(D) \| - \overline{d}_{CD}\| \le \| \| p(C) - p_C^{AB}(D) \| - \overline{d}_{CD}\| + 2\overline{\epsilon} $$

(37)

Combining (36), (37) with (38) we obtain

$$ \| \| p(C) - \hat{p}_2^*(D) \| - \overline{d}_{CD}\| < \| \| p(C) - \hat{p}^*(D) \| - \overline{d}_{CD}\| $$

(38)

(35) and (38) imply that $\hat{p}(D)$ cannot be in $H_{\overline{C}}$, i.e. $\hat{p}(D)\in H_C$.

The case $\lambda_C + 2\overline{\epsilon} < \overline{d}_{CD} \le R+\overline{\epsilon}$ can be analysed similarly to obtain that in this case $\hat{p}(D) \in H_{\overline{C}}$. This completes the proof of Proposition A.1.

In (14), it is defined that $p(D)\in R_{D_1}^{AB}$ and, thus, a flipped realization occurs when

• i $\hat{p}(D) \in H_C \quad and\; R_{D_1}^{AB} \subset H_{\overline{C}}$

• ii $\hat{p}(D) \in H_{\overline{C}}\quad and\;R_{D_1}^{AB} \subset H_C$

With this information, two support spaces can be defined for the events defined in (16) and (17) as:

$$ \begin{aligned} \Upomega' &= \{\hat{p}(D) \in H_C \cup H_{\overline{C}}\} \\ &\triangleq \left\{\overline{d}_{AD}, \overline{d}_{BD},\overline{d}_{CD}\in [0,R+\overline{\epsilon}]\mid p(A),p(B),p(C),p(D)\right\} \end{aligned} $$

(39)

$$ \zeta_{AB}' = \left\{ \begin{array}{l} \{\hat{p}(D) \in H_C\} \,\hbox{when} \,R_{D_1}^{AB} \subset H_{\overline{C}}\\ \{\hat{p}(D) \in H_{\overline{C}}\} \,\hbox{when}\, R_{D_1}^{AB} \subset H_C\\ \end{array}\right. $$

(40)

Using Proposition A.1 and assuming that $\overline{\epsilon}$ is sufficiently small, (40) can be approximated by

$$ \zeta_{AB}' \cong \left\{ \begin{array}{l} \left\{\overline{d}_{AD}, \overline{d}_{BD}\in [0,R+\overline{\epsilon}],\right.\\ \qquad\left.\overline{d}_{CD}\in [0,\lambda_C] \mid p(A),p(B),p(C),p(D)\right\}\\ \qquad\qquad\,\hbox{when}\, R_{D_1}^{AB} \subset H_{\overline{C}}\\ \\ \left\{\overline{d}_{AD}, \overline{d}_{BD}\in [0,R+\overline{\epsilon}],\right.\\ \qquad\left.\overline{d}_{CD}\in [\lambda_C,R+\overline{\epsilon}] \mid p(A),p(B),p(C),p(D)\right\} \\ \qquad\qquad\,\hbox{when}\, R_{D_1}^{AB} \subset H_C\\ \end{array}\right. $$

(41)

The measured distances $\overline{d}_{AD}, \overline{d}_{BD}$ and $\overline{d}_{CD}$ are respectively the true distances $\|p(A)-p(D)\|, \|p(B)-p(D)\|$ and $\|p(C)-p(D)\|$ blurred by additive Gaussian measurement errors ${{\mathcal{N}}(0,\sigma^2)}$ as in (1). Thus, the probability density functions $f(\overline{d}_{AD}\mid p(A),p(B),p(C),p(D)), f(\overline{d}_{BD}\mid p(A),p(B),p(C),p(D))$ and $f(\overline{d}_{CD}\mid p(A),p(B),p(C),p(D))$ of the measured distances $\overline{d}_{AD}, \overline{d}_{BD}$ and $\overline{d}_{CD}$ can be written as

$$ \begin{aligned} f(\overline{d}_{AD}\mid p(A),p(B),p(C),p(D))&=f(\overline{d}_{AD}\mid p(A),p(D))\\ &={{\mathcal{N}}}(\|p(A)-p(D)\|,\sigma^2)\\ f(\overline{d}_{BD}\mid p(A),p(B),p(C),p(D))&=f(\overline{d}_{BD}\mid p(B),p(D))\\ &={{\mathcal{N}}}(\|p(B)-p(D)\|,\sigma^2) \\ f(\overline{d}_{CD}\mid p(A),p(B),p(C),p(D))&=f(\overline{d}_{CD}\mid p(C),p(D))\\ &={{\mathcal{N}}}(\|p(C)-p(D)\|,\sigma^2) \end{aligned} $$

(42)

and are independent of each other. In order to keep the equations simple, the probability density functions are re-named as follows:

$$ \begin{aligned} \overline{f}(\overline{d}_{AD})\,&\triangleq\, f(\overline{d}_{AD}\mid p(A),p(B),p(C),p(D)) \\ \overline{f}(\overline{d}_{BD})\,&\triangleq\, f(\overline{d}_{BD}\mid p(A),p(B),p(C),p(D)) \\ \overline{f}(\overline{d}_{CD})\,&\triangleq\, f(\overline{d}_{CD}\mid p(A),p(B),p(C),p(D)) \end{aligned} $$

Due to the independent nature of the probability density functions $\overline{f}(\overline{d}_{AD}), \overline{f}(\overline{d}_{BD})$ and $\overline{f}(\overline{d}_{CD})$, define two binary functions δ _CD and I _CD as

$$ \begin{aligned} \delta_{CD}&=\left\{ \begin{array}{ll} 1 & {\hbox{If}\, R_{D_1}^{AB} \subset H_{\overline{C}}}\\ 0 & {\hbox{If}\, R_{D_1}^{AB} \subset H_C}\\ \end{array}\right.\\ I_{CD} &= \left\{ \begin{array}{ll} 1 & {\hbox{If}\,\overline{d}_{CD} \in [0,\hbox{min}(\lambda_C,R)]}\\ 0 & \hbox{Otherwise} \\ \end{array}\right. \end{aligned} $$

which let the probability $P(\zeta_{AB}\mid p(A),p(B),p(C),p(D))$ to be expressed as

$$ \begin{aligned} P(\zeta_{AB}\mid p(A),p(B),p(C),p(D))&= P(\zeta_{AB}'\mid p(A),p(B),p(C),p(D)) \\ &=\int\limits_{0}^{R+\overline{\epsilon}}\int\limits_{0}^{R+\overline{\epsilon}}\int\limits_{0}^{\hbox{min}(\lambda_C,R+\overline{\epsilon})}\delta_{CD}\overline{f}(\overline{d}_{CD})\hbox{d}(\overline{d}_{CD})\overline{f}(\overline{d}_{BD})\hbox{d}(\overline{d}_{BD}) \overline{f}(\overline{d}_{AD})\hbox{d}(\overline{d}_{AD}) \\ &\quad+\int\limits_{0}^{R+\overline{\epsilon}}\int\limits_{0}^{R+\overline{\epsilon}}\int\limits_{\hbox{min}(\lambda_C,R+\overline{\epsilon})}^{R+\overline{\epsilon}}(1-\delta_{CD}) \overline{f}(\overline{d}_{CD})\hbox{d}(\overline{d}_{CD})\overline{f}(\overline{d}_{BD})\hbox{d}(\overline{d}_{BD})\overline{f}(\overline{d}_{AD})\hbox{d}(\overline{d}_{AD}) \\ &=\int\limits_{0}^{R+\overline{\epsilon}} \int\limits_{0}^{R+\overline{\epsilon}} \int\limits_{0}^{R+\overline{\epsilon}} \left ((\delta_{CD} I_{CD})+((1-\delta_{CD})(1-I_{CD}))\right )\overline{f}(\overline{d}_{CD})\hbox{d}(\overline{d}_{CD})\overline{f}(\overline{d}_{BD})\hbox{d}(\overline{d}_{BD}) \overline{f}(\overline{d}_{AD})\hbox{d}(\overline{d}_{AD}). \\ \end{aligned} $$

(43)

B Calculation of A _S

The neighbor geometry p(A)p(B)p(C) and the transmission range R determines the area A _S where the sensor s _D could be placed. The possible neighbor geometry p(A)p(B)p(C) could be divided into two groups as shown in Fig. 12. The following calculation of A _S considered the neighbor geometries p(A)p(B)p(C) in the group $\|p(C)-P_1\|<R$. The same argument can be applied to the neighbor geometries p(A)p(B)p(C) in the other group $\|p(C)-P_1\|\ge R$. The area A _S for placement of sensor s _D can be divided into three circle segments and a triangle as illustrated in the Fig. 12(a) and calculated as

• (i)
  $$ \begin{aligned} A_1 &= \hbox{area of segment}\, P_1Q_1 \\ &= R^2 \sin^{-1}\frac{\|P_1-Q_1\|}{2R}-\frac{R^2} {2}\sin\left(2\sin^{-1}\frac{\|P_1-Q_1\|}{2R}\right) \end{aligned} $$
• (ii)
  $$ \begin{aligned} A_2 &= \hbox{area of segment}\, Q_1R_1 \\ &= R^2 \sin^{-1}\frac{\|Q_1-R_1\|}{2R}-\frac{R^2} {2}\sin\left(2\sin^{-1}\frac{\|Q_1-R_1\|}{2R}\right) \end{aligned} $$
• (iii)
  $$ \begin{aligned} A_3 &= \hbox{area of segment}\, P_1R_1 \\ &= R^2 \sin^{-1}\frac{\|P_1-R_1\|}{2R}-\frac{R^2} {2}\sin\left(2\sin^{-1}\frac{\|P_1-R_1\|}{2R}\right) \end{aligned} $$
• (iv)
  $$ \begin{aligned} A_4 &= \hbox{area of}\, \triangle P_1Q_1R_1\\ &= \sqrt{s(s-\|P_1-Q_1\|)(s-\|Q_1-R_1\|)(s-\|P_1-R_1\|)} \end{aligned} $$

where $s=\frac{\|P_1-Q_1\|+\|Q_1-R_1\|+\|P_1-R_1\|}{2}$

Fig. 12

The area in which sensor s _D can be placed such that D is a neighbor to all three sensors s _A , s _B and s _C . Here P ₁ and P ₂ are the intersection points of circles ${{\mathcal{C'}}(p(A),R)}$ with center p(A) and radius R and ${{\mathcal{C'}}(p(B),R)}$ with center p(B) and radius R

Thus the possible area for placement of D

$$ A_S=A_1+A_2+A_3+A_4 $$

(44)