On the relay selection for cooperative wireless networks with physical-layer network coding

Abstract

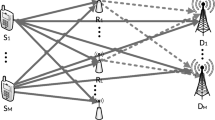
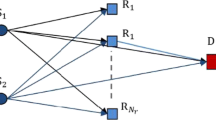
In this paper, we investigate a large cooperative wireless network with relay nodes, in which cooperation is enabled through physical-layer network coding (PLNC). Specifically, we study the impact of the relay selection on the network capacity with power constraints in two scenarios. First, we consider the basic PLNC model (a.k.a., the ARB model), in which one pair of source nodes (A, B) exchange messages via a selected relay node (R). Given the power constraint, we derive the optimal relay selection and power allocation that maximize the sum capacity, defined as the summation of the capacity for two source-destination channels. Based on results obtained above, we then consider a more general scenario with multiple pairs of source nodes. Assuming the constant power constraint, we derive the upper bound of the minimal sum capacity of any source pair. The optimal power allocation among multiple source pairs is also derived. To validate these theoretical results, we also provide two relay selection strategies: a modified optimal relay assignment strategy and a novel middle point strategy for maximizing the minimal sum capacity of any source pair.

Appendices

Appendix 1

Here we give the detailed proof of Lemma 2 in Sect. 3 Considering a relay node R that resides along line AO, we denote d _AR  = d, d ≤ s. Then d _BR  = 2s − d and $\gamma=\frac{2s-d}{d}.$ According to the problem defined in (7), we aim to find the optimal d to maximize: $C_{trans}=\min\{1+\frac{P_A}{d^n\sigma^2}, 1+\frac{P_R}{(2s-d)^n\sigma^2}\}\times \min\{1+\frac{P_B}{(2s-d)^n\sigma^2}, 1+\frac{P_R}{d^n\sigma^2}\}.$ For the problem solving, it needs to analyze four cases: (1)$\frac{P_A}{d^n}\leq \frac{P_R}{(2s-d)^n}, \frac{P_B}{(2s-d)^n}\leq \frac{P_R}{d^n};$ (2)$\frac{P_A}{d^n}\le\frac{P_R}{(2s-d)^n},\frac{P_B}{(2s-d)^n}\le\frac{P_R}{d^n};$ (3)$\frac{P_A}{d^n}\ge\frac{P_R}{(2s-d)^n},\frac{P_B}{(2s-d)^n}\le\frac{P_R}{d^n};$ (4)$\frac{P_A}{d^n}\ge\frac{P_R}{(2s-d)^n},\frac{P_B}{(2s-d)^n}\ge\frac{P_R}{d^n}.$

Typically, when the relay node locates at the middle point O with d = s and with $P_A=P_B=P_R=\frac{P}{3},$ we have $C_{trans}^*=1+\frac{2P}{3s^n\sigma^2}+\frac{P^2}{9s^{2n}\sigma^4}.$ We aim to prove that such C ^* _trans is the maximal value that can only be achieved at the middle point O. The details of the analysis of above four cases are shown as follows.

Case (1): We denote C _trans as

$$ C_1 = 1 + \frac{P_A}{d^n\sigma^2} + \frac{P_B}{(2s-d)^n\sigma^2} + \frac{P_AP_B}{d^n(2s-d)^n\sigma^4} $$

(11)

Note in this case, P _R is not the bottleneck. There are only two subcases to maximize C ₁: (1) $P_A = \left(\frac{d}{2s-d}\right)^nP_R;$ (2) $P_B = \left(\frac{2s-d}{d}\right)^nP_R.$ We first consider the subcase $P_A = \left(\frac{d}{2s-d}\right)^nP_R,$ which yields $P_B=P-P_R-P_A=P-\left[ 1+\frac{d^n}{(2s-d)^n}\right]P_R\leq \frac{(2s-d)^n}{d^n}P_R.$ Hence, we have

$$ \begin{aligned} C_1 =& \left(1+\frac{P_A}{d^n\sigma^2}\right)\left(1+\frac{P_B} {(2s-d)^n\sigma^2}\right)\\ =& \left[1+\frac{P_R}{(2s-d)^n\sigma^2}\right] \cdot \left[1+\frac{P}{(2s-d)^n\sigma^2} -\frac{(2s-d)^n+d^n}{(2s-d)^{2n}\sigma^2}P_R\right] \end{aligned} $$

(12)

For a given P, Eq. 12 is maximized with P ^* _R where $P_R^* = (P-d^n\sigma^2)\frac{(2s-d)^n}{2\left[(2s-d)^n+d^n\right]}$ which gives $P_A^* = (P-d^n\sigma^2)\frac{d^n}{2\left[(2s-d)^n+d^n\right]}, P_B^* = \frac{P+d^n\sigma^2}{2}.$ Hence, we have

$$ \begin{aligned} C_1^* =& \left[1 + \frac{P-d^n}{2\left[d^n+(2s-d)^n\right]\sigma^2}\right] \left[1+\frac{P+d^n}{2(2s-d)^n\sigma^2}\right]\\ =& \left[1+\frac{P}{2\left[d^n+(2s-d)^n\right]\sigma^2}\right] \left[1+\frac{P}{2(2s-d)^n\sigma^2}\right]+ \frac{d^{2n}}{4(2s-d)^n\left[d^n+(2s-d)^n\right]\sigma^2} \end{aligned} $$

(13)

Since d ≤ s, it is easy to show that d ⁿ + (2s − d)ⁿ monotonically decreases with the increase of d, which shows that C ^*₁ is monotonically increasing with d. We then conclude that C ^*₁ achieve the maximum when d = s and ${C_1^*}_{max} = \left(1+\frac{P-s^n}{4s^n\sigma^2}\right)\left(1+\frac{P+s^n} {2s^n\sigma^2}\right).$ It is easy to show that ${C_1^*}_{max} < C_{trans}^* = 1 + \frac{2P}{3s^n\sigma^2}+\frac{P^2}{9s^{2n}\sigma^2}.$

Next, we consider the subcase of $P_B=\left(\frac{2s-d}{d}\right)^nP_R,$ which immediately gives us $P_A=P-P_R-P_B=P-\left[1+\left(\frac{2s-d}{d}\right)^n\right]P_R \le \frac{d}{(2s-d)})^nP_R.$ Therefore, we have $P_R \geq \frac{P}{1+\left(\frac{d}{2s-d}\right)^n+ \left(\frac{2s-d}{d}\right)^n}$ and

$$ \begin{aligned} C_1 =&\left(1+\frac{P_A}{d^n\sigma^2}\right) \left(1+\frac{P_B}{(2s-d)^n\sigma^2}\right)\\ =& \left(1+\frac{P}{d^n\sigma^2}-\frac{d^n+(2s-d)^n} {d^{2n}\sigma^2}P_R\right) \cdot \left(1+\frac{P_R} {d^n\sigma^2}\right). \end{aligned} $$

(14)

To maximize Eq. 14, we have $P_R^{\Updelta} = \frac{d^n}{2\left[(2s-d)^n+d^n\right]}\left[P-(2s-d)^n\sigma^2\right].$ We can show that for $P_R^{\Updelta}$, the corresponding $C_1^\Updelta \leq C_1^*$ in Eq. 13, thus $C_1^\Updelta\leq C_{trans}^*$. In all, C ₁ ≤ C ^* _trans .

Case (2): We denote C _trans as C ₂. Since P _B is not the bottleneck there are only two cases to maximize $C_2: 1) P_A = \left(\frac{d}{2s-d}\right)^nP_R; 2) P_R = \left(\frac{d}{2s-d}\right)^nP_B.$ With the similar approach shown in case (1), we can prove that C ₂ ≤ C ^* _trans .

Case (3): We denote C _trans as $C_3=1+\frac{P_R}{(2s-d)^n\sigma^2}+\frac{P_B}{(2s-d)^n\sigma^2} +\frac{P_RP_B}{(2s-d)^{2n}\sigma^4}.$ It is easy to see that the C ₃ will increase with d and will reach the maximum when d = s no matter how the power budget is allocated among the three nodes.

Case (4): We denote C _trans as $C_4=1+\frac{P_R}{d^n\sigma^2}+\frac{P_R}{(2s-d)^n\sigma^2} +\frac{P_R^2}{d^n(2s-d)^n\sigma^4}.$ Obviously in such case, $P=P_A+P_B+P_R\ge \frac{d^n}{(2s-d)^n}P_R+\frac{(2s-d)^n}{d^n}P_R+P_R$ so that $P_R\le \frac{P}{1+(\frac{d}{2s-d})^n+(\frac{2s-d}{d})^n}.$ Therefore, we have

$$ \begin{aligned} C_4 \le &1+\frac{\frac{1}{d^n\sigma^2}+\frac{1}{(2s-d)^n\sigma^2}}{1+(\frac{d}{2s-d})^n+(\frac{2s-d}{d})^n}\times P+\left(\frac{1}{1+(\frac{d}{2s-d})^n+(\frac{2-d}{d})^n}\right)^2\frac{1}{d^n(2-d)^n\sigma^4}\times P^2\\ \le&1+\frac{2P}{3s^n\sigma^2}+\frac{P^2}{9s^{2n}\sigma^4}\end{aligned} $$

(15)

which yields C ₄ ≤ C ^* _trans . In all, considering relay nodes that reside along line AO, C ^* _trans can only be achievable when the relay is at the middle point O, which is the best relay selection.

Appendix 2

Here we give the detailed proof of Theorem 2 in Sect. 3 To solve the problem defined in Eq. 4, it can apply the convex optimization technique after certain problem transformation. In particular, we define two assistant non-negative variables C ₁ and C ₂ as $C_1=\min \{\log(1+\frac{P_A}{d^n\sigma^2}), \log(1+\frac{P_{R^i}}{\gamma^nd^n\sigma^2})\}$ and $C_2=\min \{\log(1+\frac{P_B}{\gamma^nd^n\sigma^2}), \log(1+\frac{P_{R^i}}{d^n\sigma^2})\}.$ Then the problem can be transformed into the convex problem as follows.

$$ min: \;-(C_1+C_2) $$

subject to:

$$ \left\{ \begin{array}{l} C_1-\log\left(1+\frac{P_A}{d^n\sigma^2}\right)\le 0, \;\;C_1-\log\left(1+\frac{P_{R^i}}{\gamma^nd^n\sigma^2}\right)\le 0,\\ C_2-\log\left(1+\frac{P_B}{\gamma^nd^n\sigma^2}\right)\le 0, \;\;C_2-\log\left(1+\frac{P_{R^i}}{d^n\sigma^2}\right)\le 0,\\ P_A+P_B+P_{R^i}-P=0,\\ -P_A,-P_B,-P_{R^i},-C_1,-C_2\le 0. \end{array} \right. $$

(16)

Obviously, we have the Lagrangian function as $L=-C_1-C_2+\lambda_1(C_1-\log(1+\frac{P_A}{d^n\sigma^2})) +\lambda_2(C_1-\log(1+\frac{P_{R^i}}{\gamma^nd^n\sigma^2})) +\lambda_3(C_2-\log(1+\frac{P_B}{\gamma^nd^n\sigma^2})) +\lambda_4(C_2-\log(1+\frac{P_{R^i}}{d^n\sigma^2})) +\lambda_5(-C_1)+\lambda_6(-C_2)+\lambda_7(-P_A)+\lambda_8(-P_B) +\lambda_9(-P_{R^i})+v_1(P_A+P_B+P_{R^i}-P)$ where $\lambda_i\ge 0, i=1,2,\ldots,9.$ According to the complementary slackness related to the convex optimization, it’s easy to derive that $\lambda_5,\ldots,\lambda_9$ is 0. Moreover, by applying the KKT optimality conditions in the convex optimization [25], we will have to take the partial derivative of L with respect to each of five variables and set each derivation to 0. The whole equation set related to the KKT conditions is shown as follows:

$$ \left\{ \begin{array}{l} \lambda_1\left(C_1-\log(1+\frac{P_A}{d^n\sigma^2})\right)=0; \;\;\lambda_2\left(C_1-\log(1+\frac{P_{R^i}}{\gamma^nd^n\sigma^2})\right)=0;\\ \lambda_3\left(C_2-\log(1+\frac{P_B}{\gamma^nd^n\sigma^2})\right)=0; \;\;\lambda_4\left(C_2-\log(1+\frac{P_{R^i}}{d^n\sigma^2})\right)=0;\\ \frac{\partial L}{\partial C_1}=-1+\lambda_1+\lambda_2=0;\\ \frac{\partial L}{\partial C_2}=-1+\lambda_3+\lambda_4=0;\\ \frac{\partial L}{\partial P_A}=-\lambda_1\frac{1}{\left(1+\frac{P_A}{d^n\sigma^2}\right)ln2}\frac{1}{d^n\sigma^2}+v_1=0;\\ \frac{\partial L}{\partial P_B}=-\lambda_3\frac{1}{\left(1+\frac{P_B}{\gamma^nd^n\sigma^2}\right)ln2}\frac{1}{\gamma^nd^n\sigma^2}+v_1=0;\\ \frac{\partial L}{\partial P_{R^i}}=-\lambda_2\frac{1}{\left(1+\frac{P_{R^i}}{\gamma^nd^n\sigma^2}\right)ln2}\frac{1}{\gamma^nd^n\sigma^2} -\lambda_4\frac{1}{\left(1+\frac{P_{R^i}}{d^n\sigma^2}\right)ln2}\frac{1}{d^n\sigma^2}+v_1=0;\\ C_1-\log\left(1+\frac{P_A}{d^n\sigma^2}\right)\le 0; \;\;C_1-\log\left(1+\frac{P_{R^i}}{\gamma^nd^n\sigma^2}\right)\le 0;\\ C_2-\log\left(1+\frac{P_B}{\gamma^nd^n\sigma^2}\right)\le 0; \;\;C_2-\log\left(1+\frac{P_{R^i}}{d^n\sigma^2}\right)\le 0;\\ P_A+P_B+P_{R^i}-P=0;\\ \lambda_1,..,\lambda_4, P_A,P_B,P_{R^i} \ge 0. \end{array} \right. $$

(17)

By solving the above equation set, the optimal power allocation and the corresponding maximal sum capacity can be obtained as in Theorem 2.