Outage Performance of Underlay Cognitive Opportunistic Multi-relay Networks in the Presence of Interference from Primary User

Abstract

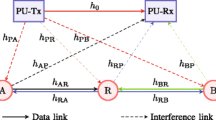
In this paper, considering the interferences from primary transmitter to secondary receiver and from secondary transmitter to primary receiver, we derive the upper and lower bounds of outage probability for underlay cognitive opportunistic multi-relay networks. Theoretical and simulation results show the upper and lower bounds converge to the exact outage probability at high interference-to-noise (INR) region. Because the interference from primary transmitter to secondary receiver is considered, an outage floor at high signal-to-noise ratio (SNR) occurs when INR increases proportionally with SNR.

Appendices

Appendix 1: Proof of Lemma 4

Note that $I_4$ in (10) can be rewritten as

$$\begin{aligned} I_4=\int \!\!\int \!\!\int _{\varOmega _1}\psi (x,y,z)dxdydz \end{aligned}$$

(22)

where

$$\begin{aligned} \psi (x,y,z)&= \text{ Pr }\left[ \frac{\gamma g_{sd}}{\gamma _I y x}+\frac{v}{\gamma _I x}< \gamma _{\text{ th }}\right] f_V(v)f_X(x)f_Y(y) \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} \ge \gamma _{\text{ th }}\right] \nonumber \\&\prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} < \gamma _{\text{ th }} \right] \end{aligned}$$

(23)

and $\varOmega _1=\{\gamma /\gamma _Q \le y < \infty , \text{ ABDE }\}$. It is noted that $0 \le \psi (x,y,z)<\infty$ and $\psi (x,y,z)$ is a continuous function. According to additivity of integration on intervals [20, Theorem 6.12], the integral $\int \!\!\int \!\!\int _{\varOmega _1}\psi (x,y,z)dxdydz$ increases with the increase of the area of $\varOmega _1$ when $\varOmega _1\in \varOmega =\{ 0 \le x,y,z<\infty \}$. Thus, by enlarging the integration region from $\varOmega _1$ to $\varOmega _2=\{\gamma /\gamma _Q \le y < \infty , \text{ AOE }\}$ shown in Fig. 2 and interchanging the order of integration, $I_4$ is upper bounded by

$$\begin{aligned} I_4^{\text{ UB }}&= \int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty } \int \limits _{0}^{\infty }\underbrace{\int \limits _{\frac{v}{\gamma _{\text{ th }}\gamma _{I}}}^{\infty } \text{ Pr }\left[ g_{sd}<\frac{(\gamma _{I}\gamma _{\text{ th }}x-v)y}{\gamma }\right] f_X(x)dx}_{\varphi } \nonumber \\&\quad \cdot f_V(v)dv \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} \ge \gamma _{\text{ th }}\right] \prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} < \gamma _{\text{ th }} \right] f_Y(y)dy. \end{aligned}$$

(24)

Integrating with respect to $x,\, \varphi$ is expressed as

$$\begin{aligned} \varphi =\left[ 1-\frac{1}{\frac{\lambda _{sd}\gamma _{\text{ th }}\gamma _{I}y}{\lambda _{cd}\gamma }+1}\right] \exp \left( -\frac{\lambda _{cd}(v-\gamma _{\text{ th }})}{\gamma _{\text{ th }}\gamma _{I}}\right) \end{aligned}$$

(25)

where the correlation between $Y$ and $V$ is decoupled due to the integration regions enlarging. Substituting (4) and (25) into (24), $I_4$ is expressed as

$$\begin{aligned} I_4^{\text{ UB }}=J_1 \cdot J_2, \end{aligned}$$

(26)

where

$$\begin{aligned} J_1&= \int \limits _{0}^{\infty }\exp \left( -\frac{\lambda _{cd}(v-\gamma _{\text{ th }})}{\gamma _{\text{ th }} \gamma _I}\right) dF_{V}(v), \end{aligned}$$

(27)

$$\begin{aligned} J_2&= \int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty }\frac{y}{y+a_2} \bigg ( 1-\frac{b_2}{y+b_2}e^{-\frac{\lambda _{sr}\gamma _{\text{ th }} y}{\gamma }}\bigg )^{K-l} \bigg (\frac{b_2}{y+b_2}e^{-\frac{\lambda _{sr}\gamma _{\text{ th }} y}{\gamma }}\bigg )^l \lambda _{sp}e^{-\lambda _{sp}y}dy \end{aligned}$$

(28)

in which $a_2=\frac{\lambda _{cd}\gamma }{\lambda _{sd}\gamma _{th}\gamma _{I}}$ and $b_2=\frac{\lambda _{cr}\gamma }{\lambda _{sr}\gamma _{th}\gamma _{I}}$. Using Lemma 3, $J_1$ can be expressed as

$$\begin{aligned} J_1=\exp \left( \lambda _{cd}/\gamma _I \right) \mathcal K (0,\infty , \lambda _{cd}/(\gamma _{\text{ th }}\gamma _I) ). \end{aligned}$$

(29)

Using the binomial theorem, $J_2$ is given as

$$\begin{aligned} J_2=\int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty } \sum \limits _{k=0}^{K-l}\sum \limits _{n=0}^{1}\left( {\begin{array}{c}K-l\\ k\end{array}}\right) \left( {\begin{array}{c}1\\ n\end{array}}\right) (-1)^{k+n} \left( \frac{a_2}{y+a_2}\right) ^n \left( \frac{b_2}{y+b_2}e^{-\frac{\lambda _{sr}\gamma _{\text{ th }}y }{\gamma }}\right) ^{k+l}\lambda _{sp}e^{-\lambda _{sp}y}dy.\nonumber \\ \end{aligned}$$

(30)

By invoking Lemma 2, $J_2$ can be obtained as

$$\begin{aligned} J_2&=\sum \limits _{k=0}^{K-l}\sum \limits _{n=0}^{1}\left( {\begin{array}{c}K-l\\ k\end{array}}\right) \left( {\begin{array}{c}1\\ n\end{array}}\right) (-1)^{k+n}\lambda _{sp}a_{2}^{n} b_{2}^{k+l} \mathcal{L }\left( \frac{\gamma }{\gamma _{Q}},a_2,b_2,n,k+l, \frac{\lambda _{sr}\gamma _{\text{ th }}(k+l)}{\gamma } +\lambda _{sp}\right) . \end{aligned}$$

(31)

Substituting (29) and (31) into (26), the upper bound of $I_4$ is obtained.

Furthermore, by shrinking the integration region of $I_4$ to $\varOmega _3=\{\gamma /\gamma _Q \le y < \infty , \text{ ABCDE }\}$, $I_4$ is lower bounded by

$$\begin{aligned} I_4^{\text{ LB }}=O_1+O_2, \end{aligned}$$

(32)

where

$$\begin{aligned} O_1=&\int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty } \int \limits _{0}^{\gamma _{\text{ th }}}\int \limits _{\frac{v+\gamma _{\text{ th }}}{\gamma _{\text{ th }}\gamma _{I}}}^{\infty } \text{ Pr }\left[ g_{sd}<\frac{(\gamma _{I}\gamma _{\text{ th }}x-v)y}{\gamma }\right] f_X(x)dx f_V(v)dv \nonumber \\&\cdot \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} \ge \gamma _{\text{ th }}\right] \prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} < \gamma _{\text{ th }} \right] f_Y(y)dy, \end{aligned}$$

(33)

$$\begin{aligned} O_2=&\int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty } \int \limits _{\gamma _{\text{ th }}}^{\infty }\int \limits _{\frac{v}{\gamma _{\text{ th }}\gamma _{I}}}^{\infty } \text{ Pr }\left[ g_{sd}<\frac{(\gamma _{I}\gamma _{\text{ th }}x-v)y}{\gamma }\right] f_X(x)dx f_V(v)dv \nonumber \\&\cdot \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} \ge \gamma _{\text{ th }}\right] \prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} < \gamma _{\text{ th }} \right] f_Y(y)dy. \end{aligned}$$

(34)

Following the derivation of $I_4^{\text{ UB }}$, we obtain $O_1=O_3 \cdot O_4$ and $O_2=O_5 \cdot J_2$, where

$$\begin{aligned} O_3&= \mathcal K \left( 0,\gamma _{\text{ th }}, \lambda _{cd}/(\gamma _{\text{ th }}\gamma _I) \right) , \end{aligned}$$

(35)

$$\begin{aligned} O_4&= \sum \limits _{k=0}^{K-l}\sum \limits _{n=0}^{1}\left( {\begin{array}{c}K-l\\ k\end{array}}\right) \left( {\begin{array}{c}1\\ n\end{array}}\right) (-1)^{k+n}\lambda _{sp}a_{2}^{n} b_{2}^{k+l} \nonumber \\&\quad \cdot \mathcal{L }\left( \frac{\gamma }{\gamma _{Q}},a_2,b_2,n,k+l, \frac{\lambda _{sd}\gamma _{\text{ th }}n}{\gamma } +\frac{\lambda _{sr}\gamma _{\text{ th }}(k+l)}{\gamma } +\lambda _{sp}\right) ,\end{aligned}$$

(36)

$$\begin{aligned} O_5&= \exp \left( \lambda _{cd}/\gamma _I \right) \mathcal K (\gamma _{\text{ th }},\infty , \lambda _{cd}/(\gamma _{\text{ th }}\gamma _I) ). \end{aligned}$$

(37)

Substituting (35)-(37) into (32), the lower bound of $I_4$ is obtained.

Appendix 2: Proof of Theorem 1

From (16) and (17), the outage gap between the lower and upper bounds is formulated as

$$\begin{aligned} P_{\text{ out }}^{\text{ UB }}-P_{\text{ out }}^{\text{ LB }}&= \sum _{l=0}^K \left( {\begin{array}{c}K\\ l\end{array}}\right) \left( I_4^{\text{ UB }}-I_4^{\text{ LB }}\right) \nonumber \\&= \sum _{l=0}^K \left( {\begin{array}{c}K\\ l\end{array}}\right) \underbrace{\int \!\!\int \!\!\int _{\varOmega _2-\varOmega _3}\psi (x,y,z)dxdydz}_{\varDelta I_4}. \end{aligned}$$

(38)

It is noted that $\varOmega _2-\varOmega _3=\{\gamma /\gamma _Q \le y < \infty , \text{ BODC }\}$ and interchanging the order of integration, $\varDelta I_4$ can be expressed as

$$\begin{aligned} \varDelta I_4&= \int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty } \int \limits _{0}^{\gamma _{\text{ th }}}\underbrace{\int _{\frac{v}{\gamma _{\text{ th }}\gamma _{I}}}^{\frac{v+\gamma _{\text{ th }}}{\gamma _{\text{ th }}\gamma _{I}}} \text{ Pr }\left[ g_{sd}<\frac{(\gamma _{I}\gamma _{\text{ th }}x-v)y}{\gamma }\right] f_X(x)dx}_{\chi } \nonumber \\&\quad \cdot f_V(v)dv \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} \ge \gamma _{\text{ th }}\right] \prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} < \gamma _{\text{ th }} \right] f_Y(y)dy. \end{aligned}$$

(39)

Integrating with respect to $x,\, \chi$ is expressed as

$$\begin{aligned} \chi =\frac{\lambda _{sd}\gamma _{\text{ th }}\gamma _I y}{\lambda _{sd}\gamma _{\text{ th }}\gamma _I y+\lambda _{cd}\gamma }e^{-\frac{\lambda _{cd}(\gamma _{\text{ th }}-v)}{\gamma _{\text{ th }}\gamma _I}}- e^{-\frac{\lambda _{cd} v}{\gamma _{\text{ th }}\gamma _I}} \left( 1-\frac{\lambda _{cd}\gamma }{\lambda _{sd}\gamma _{\text{ th }}\gamma _I y+\lambda _{cd}\gamma }e^{-\frac{\lambda _{sd}\gamma _{\text{ th }} y}{\gamma }}\right) . \end{aligned}$$

(40)

When $\gamma$ and $\gamma _{Q}$ are fixed, $\gamma _I \rightarrow \infty$, using the Taylor expansion, $\chi$ is approximated as

$$\begin{aligned} \chi \approx \left[ \frac{\lambda _{cd}(\gamma _{\text{ th }}-v)}{\gamma _{\text{ th }}}-\frac{\lambda _{cd}\gamma }{\lambda _{sd}\gamma _{\text{ th }}y}\left( 1-e^{-\frac{\lambda _{sd}\gamma _{\text{ th }} y}{\gamma }}\right) \right] \frac{1}{\gamma _I}. \end{aligned}$$

(41)

Substituting (41) into (39), we obtain

$$\begin{aligned} \lim _{\gamma _I \rightarrow \infty } \varDelta I_4=0, \end{aligned}$$

(42)

which implies $\mathop {\lim }\limits _{\gamma _I \rightarrow \infty } \left( P_{out}^{\text{ UB }}-P_{out}^{\text{ LB }} \right) =0$. When $\rho =\gamma /\gamma _{I}$ and $\rho _Q=\gamma _{Q}/\gamma _I$ are fixed, the similar result can be obtained.