Resource Allocation and Adaptive Modulation in Uplink SC-FDMA Systems

Abstract

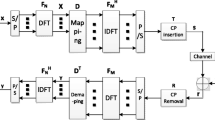
In this paper, we study joint power and sub-channel allocation, and adaptive modulation in Single Carrier Frequency Division Multiple Access (SC-FDMA) which is adopted as the multiple access scheme for the uplink in the 3GPP-LTE standard. A sum-utility maximization problem is considered. Unlike OFDMA, in addition to the restriction of allocating a sub-channel to one user at most, the multiple sub-channels allocated to a user in SC-FDMA should be consecutive as well. This renders the resource allocation problem prohibitively difficult and the standard optimization tools (e.g., Lagrange dual approach widely used for OFDMA, etc.) can not help towards its optimal solution. We propose a novel optimization framework for the solution of this problem which is inspired from the recently developed canonical duality theory. We first formulate the optimization problem as binary-integer programming problem, and then transform this binary-integer programming problems into a continuous space canonical dual problem that is a concave maximization problem. Based on the solution of the continuous space dual problem, we derive joint power and sub-channel allocation algorithm whose computational complexity is polynomial. We provide conditions under which the proposed algorithms are optimal. We also propose an adaptive modulation scheme which selects an appropriate modulation strategy for each user. We compare the proposed algorithm with the existing algorithms in the literature to assess their performance. The results show a tremendous performance gain.

Appendix

1.1 Proof of Theorem 4.1

Note that the proof of this theorem can be directly obtained from the proof given in [28] but we provide it for the completeness of the paper. We introduce Lagrange multipliers to relax the strict inequality constraints $(\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)>0$ in $\chi ^*_{\sharp }$. We recall that the canonical dual method is completely different from the Lagrange dual method and the Lagrange multipliers has nothing to do with the formulation of the canonical dual problem but are used here to prove that the primal and the corresponding conical dual problem have the same KKT points. Let $(\varvec{\delta }^{\varvec{\epsilon }^*},\varvec{\delta }^ {\varvec{\lambda }^*}, \varvec{\delta }^{\varvec{\rho }^*})\in (\mathbb {R}^N, \mathbb {R}^K,\mathbb {R}^{KJ})$ be the Lagrange multipliers associated to the inequality constraints $(\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)>0$, then the Lagrangian associated to the complementarity function $\Xi (\mathbf i ,\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)$ can be defined as follows:

$$\begin{aligned} L(\mathbf i ,\varvec{\epsilon }^*,\varvec{\lambda }^*, \varvec{\rho }^*,\varvec{\delta }^{\varvec{\epsilon }^*}, \varvec{\delta }^{\varvec{\lambda }^*},\varvec{\delta }^ {\varvec{\rho }^*}) =\Xi (\mathbf i ,\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*) + {\varvec{\epsilon }^*}^T\varvec{\delta }^{\varvec{\epsilon }^*}+ {\varvec{\lambda }^*}^T\varvec{\delta }^{\varvec{\lambda }^*}+ {\varvec{\rho }^*}^T\varvec{\delta }^{\varvec{\rho }^*} \end{aligned}$$

(40)

The KKT conditions of the primal problem are:

$$\begin{aligned} \frac{\partial L}{\partial \mathbf i }&= 0 \quad \Rightarrow \quad 2\overline{\rho }^*_{k,j}\overline{i}_{k,j} +\left( \overline{\lambda }^*_k-\overline{\rho }^*_{k,j}-U_{k,j}+ \sum _{n=1}^N\overline{\epsilon }^*_nA^k_{n,j}\right) = 0, \quad \forall k,j\end{aligned}$$

(41)

$$\begin{aligned} \frac{\partial L}{\partial \varvec{\epsilon }^*}&= 0 \quad \Rightarrow \quad \sum _{k=1}^K\sum _{j=1}^J A^k_{n,j}\overline{i}_{k,j} - 1 + \delta ^{\varvec{\epsilon }^*}_n = 0, \quad \forall n\end{aligned}$$

(42)

$$\begin{aligned} \frac{\partial L}{\partial \varvec{\lambda }^*}&= 0 \quad \Rightarrow \quad \sum _{j=1}^J \overline{i}_{k,j} - 1 + \delta ^{\varvec{\lambda }^*}_k = 0, \quad \forall k\end{aligned}$$

(43)

$$\begin{aligned} \frac{\partial L}{\partial \varvec{\rho }^*}&= 0 \quad \Rightarrow \quad \overline{i}_{k,j} (\overline{i}_{k,j}-1) + \delta ^{\varvec{\rho }^*}_{k,j} = 0, \quad \forall k,j\end{aligned}$$

(44)

$$\begin{aligned}&(\varvec{\delta }^{\varvec{\epsilon }^*},\varvec{\delta }^ {\varvec{\lambda }^*}, \varvec{\delta }^{\varvec{\rho }^*}) \le 0, \quad (\overline{\varvec{\epsilon }}^*,\overline{\varvec{\lambda }}^*, \overline{\varvec{\rho }}^*)>0, \quad {\overline{\varvec{\epsilon }}^*}^T\varvec{\delta }^ {\varvec{\epsilon }^*}=0, \quad {\overline{\varvec{\lambda }}^*}^T\varvec{\delta }^ {\varvec{\lambda }^*}\!=\!0,\quad {\overline{\varvec{\rho }}^*}^T\varvec{\delta }^{\varvec{\rho }^*} =0 \nonumber \\ \end{aligned}$$

(45)

From the KKT condition (41), we get $\overline{i}_{k,j} = \frac{1}{2\overline{\rho }^*_{k,j}}\left( U_{k,j} + \overline{\rho }^*_{k,j} - \overline{\lambda }^*_k -\sum _{n=1}^N\overline{\epsilon }^*_n A^k_{n,j}\right)$. According to complementarity conditions (45), the Lagrange multipliers $(\varvec{\delta }^{\varvec{\epsilon }^*}, \varvec{\delta }^{\varvec{\lambda }^*}, \varvec{\delta }^{\varvec{\rho }^*}) = 0$ for $(\overline{\varvec{\epsilon }}^*,\overline{\varvec{\lambda }}^*, \overline{\varvec{\rho }}^*)>0$ and conditions (42–44) become

$$\begin{aligned} \sum _{k=1}^K\sum _{j=1}^J A^k_{n,j}\overline{i}_{k,j} - 1&= 0, \quad \forall n\end{aligned}$$

(46)

$$\begin{aligned} \sum _{j=1}^J \overline{i}_{k,j} - 1&= 0, \quad \forall k\end{aligned}$$

(47)

$$\begin{aligned} \overline{i}_{k,j} (\overline{i}_{k,j}-1)&= 0, \quad \forall k,j \end{aligned}$$

(48)

Replacing $\frac{1}{2\overline{\rho }^*_{k,j}}\left( U_{k,j} + \overline{\rho }^*_{k,j} - \overline{\lambda }^*_k -\sum _{n=1}^N\overline{\epsilon }^*_n A^k_{n,j}\right)$ for $\overline{i}_{k,j}$ in (46–48) leads to

$$\begin{aligned}&\sum _{k=1}^K\sum _{j=1}^J\left\{ \frac{1}{2\overline{\rho }^*_{k,j}} \left( U_{k,j} + \overline{\rho }^*_{k,j} - \overline{\lambda }^*_k - \sum _{n=1}^N\overline{\epsilon }^*_n A^k_{n,j}\right) A^k_{n,j}\right\} -1=0, \quad \forall n \end{aligned}$$

(49)

$$\begin{aligned}&\sum _{j=1}^J\left\{ \frac{1}{2\overline{\rho }^*_{k,j}}\left( U_{k,j} + \overline{\rho }^*_{k,j} - \overline{\lambda }^*_k -\sum _{n=1}^N\overline{\epsilon }^*_n A^k_{n,j}\right) \right\} -1=0, \quad \forall k\end{aligned}$$

(50)

$$\begin{aligned}&\frac{1}{2\overline{\rho }^*_{k,j}}\left( U_{k,j} + \overline{\rho }^*_{k,j} - \overline{\lambda }^*_k -\sum _{n=1}^N\overline{\epsilon }^*_n A^k_{n,j}\right) \nonumber \\&\quad \times \left\{ \frac{1}{2\overline{\rho }^*_{k,j}}\left( U_{k,j} + \overline{\rho }^*_{k,j} - \overline{\lambda }^*_k -\sum _{n=1}^N\overline{\epsilon }^*_n A^k_{n,j}\right) -1\right\} =0, \forall k,j \end{aligned}$$

(51)

which are in fact the KKT conditions of the canonical dual problem, $\mathrm {f}^d(\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)$. This proves that for $(\overline{\varvec{\epsilon }}^*,\overline{\varvec{\lambda }}^*, \overline{\varvec{\rho }}^*)\in \chi ^*_{\sharp }$ being the KKT point of $\mathrm {f}^d(\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)$, $\overline{\mathbf{i }}$ given by (26) is the KKT point of the primal problem. This establishes the first part of the theorem.

According to (20), the total complementarity function at the KKT point $(\overline{\mathbf{i }},\overline{\mathbf{x }}^*)$ can be written as

$$\begin{aligned} \Xi (\overline{\mathbf{i }},\overline{\varvec{\epsilon }}^*, \overline{\varvec{\lambda }}^*,\overline{\varvec{\rho }}^*)&= \Lambda (\overline{\mathbf{i }})^T\overline{\mathbf{x }}^*-V^{\sharp }( \overline{\mathbf{x }}^*) -\sum _{k=1}^K \,\,\sum _{j=1}^J\overline{i}_ {k,j}U_{k,j} \nonumber \\&= -\sum _{k=1}^K \,\,\sum _{j=1}^J\overline{i}_{k,j}U_{k,j}= \mathrm {f}(\overline{\mathbf{i }}) \end{aligned}$$

(52)

which is obvious from the fact that $V^{\sharp }(\overline{\mathbf{x }}^*)=0$ for $(\overline{\varvec{\epsilon }}^*,\overline{\varvec{\lambda }}^*, \overline{\varvec{\rho }}^*)>0$, and where Eqs. (46–48) imply that $\Lambda (\overline{\mathbf{i }})=0$. Similarly from (21), we have

$$\begin{aligned} \Xi (\overline{\mathbf{i }},\overline{\varvec{\epsilon }}^*, \overline{\varvec{\lambda }}^*,\overline{\varvec{\rho }}^*)&= \sum _{k=1}^K \,\,\sum _{j=1}^J\left\{ \overline{\rho }^*_{k,j}\overline{i}^2_{k,j}+\left( \overline{\lambda }^*_k-\overline{\rho }^*_{k,j}-U_{k,j}+ \sum _{n=1}^N\overline{\epsilon }^*_nA^k_{n,j}\right) \overline{i}_{k,j}\right\} \nonumber \\&-\sum _{n=1}^N\overline{\epsilon }^*_n- \sum _{k=1}^K \overline{\lambda }^*_k\nonumber \\&= -\frac{1}{4}\sum _{k=1}^K \,\,\sum _{j=1}^J\left\{ \frac{\left( U_{k,j} + \overline{\rho }^*_{k,j} - \overline{\lambda }^*_k -\sum _{n=1}^N \overline{\epsilon }^*_n A^k_{n,j}\right) ^2}{\overline{\rho }^*_{k,j}} \right\} \!-\!\sum _{n=1}^N\overline{\epsilon }^*_n- \sum _{k=1}^K \overline{\lambda }^*_k \nonumber \\&= \mathbf f ^{\,d}(\overline{\varvec{\epsilon }}^*, \overline{\varvec{\lambda }}^*,\overline{\varvec{\rho }}^*) \end{aligned}$$

(53)

This shows that the canonical dual problem is perfectly dual to the primal problem. This completes the proof.

1.2 Proof of Theorem 4.2

The total complementarity function $\Xi (\mathbf i ,\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)$ is convex in $\mathbf i$ and concave (linear) in $\varvec{\epsilon }^*$, $\varvec{\lambda }^*$ and $\varvec{\rho }^*$. Therefore, the stationary point $(\overline{\mathbf{i }},\overline{\varvec{\epsilon }}^*, \overline{\varvec{\lambda }}^*,\overline{\varvec{\rho }}^*)$ is a saddle point of $\Xi (\mathbf i ,\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)$. Furthermore, $\mathrm {f}^d(\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)$ is defined by $\Xi (\overline{\mathbf{i }},\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)$ with $\overline{\mathbf{i }}$ being a stationary point of $\Xi (\mathbf i ,\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)$ with respect to $\mathbf i \in \mathcal {I}_a$. Consequently, $\mathrm {f}^d(\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)$ is concave on $\chi ^*_{\sharp }$ and the KKT point $(\overline{\varvec{\epsilon }}^*,\overline{\varvec{\lambda }}^*, \overline{\varvec{\rho }}^*)\in \chi ^*_{\sharp }$ must be its global maximizer. Thus, by the saddle mini–max theorem:

$$\begin{aligned} \mathrm {f}^d(\overline{\varvec{\epsilon }}^*, \overline{\varvec{\lambda }}^*,\overline{\varvec{\rho }}^*)&= \max _{\varvec{\epsilon }^*> 0}\max _{\varvec{\lambda }^*> 0}\max _{\varvec{\rho }^*> 0} \mathrm {f}^d(\varvec{\epsilon }^*,\varvec{\lambda }^*, \varvec{\rho }^*)\nonumber \\&= \max _{\varvec{\epsilon }^*> 0}\max _{\varvec{\lambda }^*> 0} \max _{\varvec{\rho }^*> 0} \min _\mathbf{i \in \mathcal {I}_a } \Xi (\mathbf i ,\varvec{\epsilon }^*,\varvec{\lambda }^*, \varvec{\rho }^*)\nonumber \\&= \max _{\varvec{\epsilon }^*> 0}\max _{\varvec{\lambda }^*> 0} \max _{\varvec{\rho }^*> 0} \min _\mathbf{i \in \mathcal {I}_a} \left\{ \mathrm {f}(\mathbf i ) + \varvec{\epsilon }^T\varvec{\epsilon }^* +\varvec{\lambda }^T\varvec{\lambda }^* + \varvec{\rho }^T\varvec{\rho }^*\right\} \nonumber \\&= \max _{\varvec{\epsilon }^*> 0}\max _{\varvec{\lambda }^*> 0} \min _\mathbf{i \in \mathcal {I}_a}\left\{ \mathrm {f}(\mathbf i ) \!+ \varvec{\epsilon }^T\varvec{\epsilon }^* \!+\varvec{\lambda }^T \varvec{\lambda }^* \!+\max _{\varvec{\rho }^*> 0}\left\{ \sum _{k=1}^K \sum _{j=1}^J\rho ^*_{k,j}i_{k,j}(i_{k,j}\!-\!1)\right\} \right\} \nonumber \\&= \max _{\varvec{\epsilon }^*> 0} \min _\mathbf{i \in \mathcal {I}_a}\left\{ \mathrm {f}(\mathbf i ) + \varvec{\epsilon }^T \varvec{\epsilon }^* +\max _{\varvec{\lambda }^*> 0}\left\{ \sum _{k=1}^K \lambda ^*_k\left( \sum _{j=1}^Ji_{k,j}-1\right) \right\} \right\} \nonumber \\&\text {s.t.}\quad i_{k,j}(i_{k,j}-1)=0,\forall k,j\nonumber \\&= \min _\mathbf{i \in \mathcal {I}_a}\left\{ \mathrm {f}(\mathbf i ) + \max _{\varvec{\epsilon }^*> 0}\left\{ \sum _{n=1}^N\epsilon ^*_n\left( \sum _{k=1}^K \sum _{j=1}^Ji_{k,j}A^k_{n,j}-1\right) \right\} \right\} \nonumber \\&\text {s.t.}\quad i_{k,j}(i_{k,j}-1)=0, \forall k,j;\quad \sum _{j=1}^Ji_{k,j}=1,\forall k \nonumber \\&= \min _\mathbf{i \in \mathcal {I}_a}\mathrm {f}(\mathbf i ) \quad \text {s.t.}\left\{ i_{k,j}(i_{k,j}-1)=0,\forall k,j;\sum _{j=1}^Ji_{k,j}=1, \forall k;\right. \nonumber \\&\left. \qquad \qquad \qquad \qquad \sum _{k=1}^K \sum _{j=1}^Ji_{k,j}A^k_{n,j}=1,\forall n\right\} \nonumber \\&= \min _\mathbf{i \in \mathcal {I}_f}\mathrm {f}(\mathbf i ) \end{aligned}$$

(54)

Note that the linear programming

$$\begin{aligned} \max _{\varvec{\rho }^*> 0}\left\{ \sum _{k=1}^K\sum _{j=1}^J\rho ^*_{k,j}i_{k,j}(i_{k,j}-1)\right\} \end{aligned}$$

has a finite solution in the open domain $\chi ^*_{\sharp }$ if and only if $i_{k,j}(i_{k,j}-1)=0,\forall k,j$. By a similar argument, the solution of $\max _{\varvec{\lambda }^*> 0}\left\{ \sum _{k=1}^K \lambda ^*_k\left( \sum _{j=1}^Ji_{k,j}-1\right) \right\}$ and $\max _{\varvec{\epsilon }^*> 0}\left\{ \sum _{n=1}^N\epsilon ^*_n\right. \left. \left( \sum _{k=1}^K \sum _{j=1}^Ji_{k,j}A^k_{n,j}-1\right) \right\}$ leads to the last Eq. (54). This shows that the KKT point $(\overline{\varvec{\epsilon }}^*,\overline{\varvec{\lambda }}^*, \overline{\varvec{\rho }}^*)$ maximizes $\mathrm {f}^d(\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)$ over $\chi ^*_{\sharp }$ if and only if $\overline{\mathbf{i }}$ is the global minimizer of $\mathrm {f}(\mathbf i )$ over $\mathcal {I}_f$. This completes the proof.

1.3 Proof of Theorem 5.1

Using sub-gradient method with projection defined by (39) ensures the positive solution of KKT Eq. (38) which implies that the corresponding $i_{k,j}$ is binary integer. However, respecting the positivity constraint on $\varvec{\lambda }^*$, Eq. (37) can not ensure that a single sub-channel pattern is allocated to each user but $1+\sigma ^{\varvec{\lambda }^*}_k$ number of patterns will be allocated to each user $k$. Similarly, ensuring that $\varvec{\epsilon }^*>0$, Eq. (36) means that a sub-channel can be allocated to more than one users.

In the following, we discuss that we can find another approximate problem for which the above KKT equations not only provide binary integer solution but also ensure that a user will be assigned with a single sub-channel pattern and a sub-channel will be allocated to a single user. To this end, we proceed as follows. The KKT Eq. (38) can be written as

$$\begin{aligned} U_{k,j} - \lambda ^*_k -\sum _{n=1}^N\epsilon ^*_n A^k_{n,j}= \pm \,\, \rho ^*_{k,j}, \quad \forall k,j \end{aligned}$$

(55)

We introduce $KJ$ new variables $\theta _{k,j}$’s defined as follows

$$\begin{aligned} \theta _{k,j}= \left\{ \begin{array}{lll} \{1,0\} &{} \mathrm {if} U_{k,j} - \lambda ^*_k -\sum _{n=1}^N\epsilon ^*_n A^k_{n,j}= - \rho ^*_{k,j} \\ \{-1,0\} &{} \mathrm{ if} U_{k,j} - \lambda ^*_k -\sum _{n=1}^N\epsilon ^*_n A^k_{n,j}= + \rho ^*_{k,j} \end{array} \right. \end{aligned}$$

(56)

From the above definition of $\theta _{k,j}$, equations (55) can be written as

$$\begin{aligned} U_{k,j} -2\theta _{k,j}\rho ^*_{k,j}- \lambda ^*_k -\sum _{n=1}^N\epsilon ^*_n A^k_{n,j}= \pm \,\, \rho ^*_{k,j}, \quad \forall k,j \end{aligned}$$

(57)

Let $\widetilde{U}_{k,j}=U_{k,j} - 2\theta _{k,j}\rho ^*_{k,j}$, then the above equations take the form:

$$\begin{aligned} \widetilde{U}_{k,j}- \lambda ^*_k -\sum _{n=1}^N\epsilon ^*_n A^k_{n,j}= \pm \,\, \rho ^*_{k,j}, \quad \forall k,j \end{aligned}$$

(58)

Although the utilities are changed from $U_{k,j}$ to $\widetilde{U}_{k,j}=U_{k,j} - 2\theta _{k,j}\rho ^*_{k,j}$, the solution of the above equations provide integer solution to $i_{k,j}$’s. We now apply this change in utilities to the Eqs. (36–37). The KKT equations (37) can be written as

$$\begin{aligned} \sum _{j=1}^J\left\{ \frac{1}{2\rho ^*_{k,j}}\left( U_{k,j} - 2\theta _{k,j}\rho ^*_{k,j} + 2\theta _{k,j}\rho ^*_{k,j} + \rho ^*_{k,j} - \lambda ^*_k -\!\sum _{n=1}^N\epsilon ^*_n A^k_{n,j}\right) \right\} \!=\!1+\sigma ^{\varvec{\lambda }^*}_k, \quad \forall k\nonumber \\ \end{aligned}$$

(59)

Replacing $\widetilde{U}_{k,j}$ for $U_{k,j} - 2\theta _{k,j}\rho ^*_{k,j}$, the above equations become:

$$\begin{aligned} \sum _{j=1}^J\left\{ \frac{1}{2\rho ^*_{k,j}}\left( \widetilde{U}_{k,j}+ \rho ^*_{k,j} - \lambda ^*_k -\sum _{n=1}^N\epsilon ^*_n A^k_{n,j}\right) \right\} +\sum _{j=1}^J\theta _{k,j} =1+\sigma ^{\varvec{\lambda }^*}_k, \quad \forall k \end{aligned}$$

(60)

If there exist $\theta _{k,j}$’s such that $\sum _{j=1}^J\theta _{k,j}=\sigma ^{\varvec{\lambda }^*}_k$, then we have

$$\begin{aligned} \sum _{j=1}^J\left\{ \frac{1}{2\rho ^*_{k,j}}\left( \widetilde{U}_{k,j}+ \rho ^*_{k,j} - \lambda ^*_k -\sum _{n=1}^N\epsilon ^*_n A^k_{n,j}\right) \right\} =1, \quad \forall k \end{aligned}$$

(61)

This implies that there exist another problem with a different set of utilities for which the above solution ensures that a single pattern will be allocated to each user. By using a similar procedure for the KKT equations (36), we get

$$\begin{aligned} \sum _{k=1}^K\sum _{j=1}^J\left\{ \frac{1}{2\rho ^*_{k,j}}\left( \widetilde{U}_{k,j} + \rho ^*_{k,j} - \lambda ^*_k -\sum _{n=1}^N\epsilon ^*_n A^k_{n,j}\right) A^k_{n,j}\right\} =1, \forall n \end{aligned}$$

(62)

which enures that a sub-channel will be allocated to a single user at most when $\sum _{k=1}^K\sum _{j=1}^J\theta _{k,j}\mathbf {A}^k_{n,j}= \sigma ^{\varvec{\epsilon }^*}_n$, and the utilities are changed from $U_{k,j}$ to $\widetilde{U}_{k,j}=U_{k,j} - 2\theta _{k,j}\rho ^*_{k,j}$.

The above analysis shows that the solution of the problem $\mathcal {P}1$, namely $(\overline{\varvec{\epsilon }}^*,\overline{\varvec{\lambda }}^*, \overline{\varvec{\rho }}^*)$ that lies in the positive cone, is the solution of the above KKT Eqs. (57,61,62). Moreover, the KTT Eqs. (58,61,62) give the stationary point of a slightly modified problem $\tilde{\mathrm {f}}^d(\varvec{\epsilon }^*,\varvec{\lambda }^*, \varvec{\rho }^*)$ which is the canonical dual of a slightly modified primal problem with utilities $\widetilde{U}_{k,j}=U_{k,j} - 2\theta _{k,j}\rho ^*_{k,j}$. Since the solution $(\overline{\varvec{\epsilon }}^*,\overline{\varvec{\lambda }}^*, \overline{\varvec{\rho }}^*)$ is positive, according to Theorems 4.1 and 4.2, the proposed sub-gradient based solution proposed in Table 1 optimally solves a corresponding primal problem with utilities $\widetilde{U}_{k,j}$’s and an objective function $\tilde{\mathrm {f}}(\mathbf i )$. Note also that the canonical dual $\tilde{\mathrm {f}}^d(\varvec{\epsilon }^*,\varvec{\lambda }^*, \varvec{\rho }^*)$ is concave (since the KKT solution is in the positive cone). However, how far the solution of the modified problem will be from that of the primal problem (5) depends upon the values of $\rho _{k,j}^*$’s.

1.4 Proof of Corollary 5.1

If $\rho _{k,j}^*<<U_{k,j},\forall k,j$, then $\widetilde{U}_{k,j}\approx U_{k,j},\forall k,j$, $\tilde{\mathrm {f}}(\mathbf i )\approx \mathrm {f}(\mathbf i )$, and

$$\begin{aligned} \max _{(\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)} \tilde{\mathrm {f}}^d \approx \max _{(\varvec{\epsilon }^*,\varvec{\lambda }^*,\varvec{\rho }^*)} \mathrm {f}^d \end{aligned}$$

(63)

For $\rho _{k,j}^*<<U_{k,j},\forall k,j$, the solution of the Eqs. (57,61,62) is very close to that of Eqs. (29,30, 31). Furthermore, the solution of (58,61,62) is the optimal solution of the corresponding primal problem with utilities $\widetilde{U}_{k,j}$ (which is very close to the optimal solution of the primal problem with utilities $U_{k,j}$). Consequently, the dual canonical problem obtained using the sub-gradient based algorithm (Table 1) will provide solution to the primal problem which is very close to the optimal solution. This completes the proof.