Finding Near-Optimal Regularization Parameter for Indoor Device-free Localization

Abstract

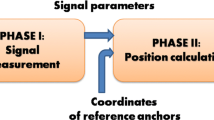
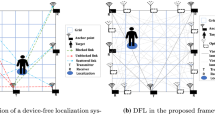
Device-free Localization (DfL) systems offer real-time indoor localization of people without any electronic devices attached on their bodies. The human body influences the radio wave propagation between wireless links and changes the Received Signal Strength (RSS). Wireless Sensor Networks (WSNs) nodes easily measure these RSS changes and appropriate Radio Tomographic Imaging (RTI) algorithms can then process the RSS data and allow human localization. This paper investigates how to choose near-optimal regularization parameter during the regularization process for indoor DfL and describes an experimental indoor DfL setup realized with a Sun SPOT based WSN. The work elaborates on the numerical calculation of the near-optimal regularization parameter by usage of the trade-off curve criterion. The calculated parameter enables conclusive RTI image with sufficient localization precision for eHealth or other ambient-assisted-living applications where the error tolerance is at a scale of several tens of centimeters. The value for the regularization parameter matches the empirical derived value obtained in the authors’previous work.

Appendix: Singular Value Decomposition, SVD and Trade-off Curve, Curvature of the Logarithmic Trade-off Curve

1.1 Singular Value Decomposition

This “Appendix” gives analytical equations derived by the trade-off curve analysis when Tikhonov regularization is employed. For common engineering problems, it is reasonable to consider that the solution is stable (does not experience severe and sudden deviations), so the assumption that ${{\varvec{P}}}$ equals identity matrix is acceptable. Since not any a priori estimate is known about the true solution, the ${{\varvec{x}}}_{0}$ vector is set to zero.

Singular value decomposition technique breaks down the $L{\times }P$ weighting matrix ${{\varvec{A}}}$ (L is the number of the links; P is the number of the pixels) onto singular vectors. When $L < P$, SVD operation results in

$$\begin{aligned} {{\varvec{A}}} = \sum _{i=1}^L {{\varvec{u}}}_{i}\sigma _{i}{{\varvec{v}}}_{i}^T, \end{aligned}$$

(10)

where ${{\varvec{u}}}_{i}$ and ${{\varvec{v}}}_{i}$ are singular vectors, and $\sigma _{i}$ are singular values with property

$$\begin{aligned} \sigma _{1}\ge \sigma _{2}\ge \cdots \ge \sigma _{L}\ge 0. \end{aligned}$$

The singular vectors ${{\varvec{u}}}_{i}$ and ${{\varvec{v}}}_{i}$ are orthogonal and unit (they are orthonormal), i.e., ${{\varvec{u}}}_{i}^T{{\varvec{u}}}_{j} = {{\varvec{v}}}_{i}^T{{\varvec{v}}}_{j} = \varvec{ \delta }_{ij}$.

The entries of the singular vectors ${{\varvec{u}}}_{i}$ and ${{\varvec{v}}}_{i}$ have property to alter between positive and negative, whereas the singular values $\sigma _{i}$ monotonically decrease to 0. Thus, if the SVD delivers larger singular values, the singular vectors experience less oscillations, and vice versa.

The least squares method is the most convenient solution for the minimization problem (7), which yields to

$$\begin{aligned} {{\varvec{x}}}_{\lambda } = \min _{{\varvec{x}}}\left\| \left( \frac{{{\varvec{A}}}}{\lambda {{\varvec{P}}}}\right) {{\varvec{x}}}-\left( \frac{{{\varvec{y}}}}{\lambda {{\varvec{P}}} {{\varvec{x}}}_{0}}\right) \right\| _{2}. \end{aligned}$$

(11)

Appling SVD to (11) gives

$$\begin{aligned} {{\varvec{x}}}_{\lambda }=\sum _{i=1}^Lf_{i}{\frac{{{\varvec{u}}}_{i}^T{{\varvec{y}}}}{\sigma _{i}}}{{\varvec{v}}}_{i}, \end{aligned}$$

(12)

where $f_{1}, f_{2},\ldots\, ,f_{L}$ are the Tikhonov filter coefficients, defined as

$$\begin{aligned} f_{i}=\frac{\sigma _{i}^2}{\sigma _{i}^2+\lambda }\,\cong\,{\left\{ \begin{array}{ll} 1, &\quad \sigma _{i}\gg \lambda \\ \sigma _{i}^2/\lambda ^2, &\quad \sigma _{i}\ll \lambda .\\ \end{array}\right. } \end{aligned}$$

(13)

For the straightforward solution ($\lambda = 0$), all coefficients $f_{i}$ become 1. When the regularization is employed ($\lambda > 0$), the filter coefficients suppress the influence of small singular values on the regularized solution ${{\varvec{x}}}_{\lambda }$.

The residual solution is given by

$$\begin{aligned} {{\varvec{y}}}-{{\varvec{Ax}}}_{\lambda }=\sum _{i=1}^L\left( 1-f_{i}\right) {{\varvec{u}}}_{i}^T{{\varvec{y}}}{{\varvec{u}}}_{i}+{{\varvec{y}}}_{0}, \end{aligned}$$

(14)

where the vector ${{\varvec{y}}}_{0}={{\varvec{y}}}-\sum _{i=1}^L{{\varvec{u}}}_{i}{{\varvec{u}}}_{i}^T{{\varvec{y}}}$ is part of ${{\varvec{y}}}$ which is not affected by the filter coefficients. Contrary to the previous case of regularized solution, the filter coefficients suppress the influence of larger singular values on the residual solution.

Regarding (12) and (14), the squares of the solution and residual norms are:

$$\begin{aligned} \left\| {{\varvec{x}}}_{\lambda }\right\| _{2}^{2}= & \sum _{i=1}^L\left( f_{i}\frac{{{\varvec{u}}}_{i}^T{{\varvec{y}}}}{\sigma _{i}}\right) ^2 \end{aligned}$$

(15)

$$\begin{aligned} \left\| {{\varvec{Ax}}}_{\lambda }-{{\varvec{y}}}\right\| _{2}^{2}= & \sum _{i=1}^L\left( \left( 1-f_{i}\right) {{\varvec{u}}}_{i}^T{{\varvec{y}}} \right) ^2. \end{aligned}$$

(16)

Equations (15) and (16), supported by (13), reveal the influence of $\lambda$ to the quality of the final regularized solution, and help to understand the rationale of the trade-off curve criterion.

1.2 SVD and Trade-off Curve

In reality, errors (donated as vector ${{\varvec{e}}}$) inevitably influence any measurement process, so the gathered data ${{\varvec{y}}}$ are

$$\begin{aligned} {{\varvec{y}}}=\bar{{{\varvec{y}}}}+{{\varvec{e}}}, \quad \bar{{{\varvec{y}}}}={{\varvec{A}}}\bar{{{\varvec{x}}}} \end{aligned}$$

(17)

where $\bar{{{\varvec{y}}}}$ are exact undisturbed measurements and $\bar{{{\varvec{x}}}}={{\varvec{A}}}^T\bar{{{\varvec{y}}}}$ is the exact solution.

Then, the regularized solution is

$$\begin{aligned} {{\varvec{x}}}_{\lambda }=\bar{{{\varvec{x}}}}_{\lambda }+{{\varvec{e}}}_{\lambda }^e, \end{aligned}$$

(18)

where $\bar{{{\varvec{x}}}}_{\lambda }=\left( {{\varvec{A}}}^{T}{{\varvec{A}}}+\lambda ^2{{\varvec{I}}}\right) ^{-1}{{\varvec{A}}}^{T}\bar{{{\varvec{y}}}}$ is part that corresponds to the exact undisturbed measurements, and ${{\varvec{x}}}_{\lambda }^e=\left( {{\varvec{A}}}^{T}{{\varvec{A}}}+\lambda ^2{{\varvec{I}}}\right) ^{-1}{{\varvec{A}}}^{T}{{\varvec{e}}}$ is part that corresponds to the pure errors.

It is assumed that for $\bar{{{\varvec{y}}}}$ applies the discrete Picard condition which states that the singular values $\sigma _{i}$ decline slower than $\left| {{\varvec{u}}}_{i}^T\bar{{{\varvec{y}}}}\right|$. A consequence of this assumption is that exact solution coefficients $\left| {{\varvec{v}}}_{i}^T\bar{{{\varvec{x}}}}\right| =\left| {{\varvec{u}}}_{i}^T\bar{{{\varvec{y}}}}/\sigma _{i}\right|$ also decline, which ensures that the exact solution has moderate and limited norm. This is essential characteristic of the realistic inverse problems which guarantees that the regularized solution would be a good approximation and it make sense to search for near-optimal $\lambda$.

Let k be the number of filter coefficients closer to 1 (e.g. greater than 0.5). Equation (13) defines that for the k-th singular value holds that $\sigma _{k}\cong \lambda$. Boundary number k divides the singular values on “big ones” and “small ones”, so it is very important for specifying the $\lambda$. By the nature of the number k and knowing that $\left| {{\varvec{v}}}_{i}^T\bar{{{\varvec{x}}}}\right|$ decline, follows that, for not too large $\lambda$, the sum in (15) mainly consists of the first k terms. Thus, the square of a solution norm of the exact undisturbed measurements $\bar{{{\varvec{y}}}}$ is

$$\begin{aligned} \left\| \bar{{{\varvec{x}}}}_{\lambda }\right\| _{2}^{2}\,\cong\, \sum _{i=1}^k\left( {{\varvec{v}}}_{i}^T\bar{{{\varvec{x}}}}\right) ^2\,\cong\, \sum _{i=1}^L\left( {{\varvec{v}}}_{i}^T\bar{{{\varvec{x}}}}\right) ^2=\left\| \bar{{{\varvec{x}}}}\right\| _{2}^2, \end{aligned}$$

(19)

as long as $\lambda$ is small enough. For (19), as $\lambda$ tends to infinity, k tends to zero, thus, $\left\| \bar{{{\varvec{x}}}}_{\lambda }\right\| _{2}$ also tends to zero. Contrary, as $\lambda$ tends to zero, $\left\| \bar{{{\varvec{x}}}}_{\lambda }\right\| _{2}$ tends to $\left\| \bar{{{\varvec{x}}}}\right\| _{2}$.

The square of a residual norm of the exact undisturbed measurements $\bar{{{\varvec{y}}}}$ is

$$\begin{aligned} \left\| {{\varvec{A}}}\bar{{{\varvec{x}}}}_{\lambda }-\bar{{{\varvec{y}}}}\right\| _{2}^2\,\cong\, \sum _{i=k}^L\left( {{\varvec{u}}}_{i}^T\bar{{{\varvec{y}}}}\right) ^2. \end{aligned}$$

(20)

For (20), as $\lambda$ tends to infinity, the residual norm tends to $\left\| \bar{{{\varvec{y}}}}\right\| _{2}$. Contrary, for small $\lambda$, the residual norm fades out.

The conclusion about the trade-off curve for the exact undisturbed measurements $\bar{{{\varvec{y}}}}$ is that it is mainly a line at $\left\| \bar{{{\varvec{x}}}}_{\lambda }\right\| _{2}\,\cong\, \left\| \bar{{{\varvec{x}}}}\right\| _{2}$, and for large values of $\lambda$, $\left\| \bar{{{\varvec{x}}}}_{\lambda }\right\| _{2}$ drops towards zero.

Below follows an analogous overview about the trade-off curve for the pure errors ${{\varvec{e}}}$. The errors that disturbance the measurements are random variables and they are not correlated each other. This means that coefficients ${{\varvec{u}}}_{i}^T{{\varvec{e}}}$ do not rely upon i,

$$\begin{aligned} \epsilon \left( \left( {{\varvec{u}}}_{i}^T{{\varvec{y}}}\right) ^2\right) =\texttt {E}, \qquad i=1,2,\ldots\, ,L, \end{aligned}$$

(21)

i.e. errors do not obey the discrete Picard condition. Thus, the square of a solution norm of the errors is

$$\begin{aligned} \left\| {{\varvec{x}}}_{\lambda }^e\right\| _{2}^2\,\cong\,& \sum _{i=1}^L \left( \frac{\sigma _{i} \texttt {E}}{\sigma _{i}^2+\lambda ^2}\right) ^2 \,\cong\,\sum _{i=1}^k\left( \frac{\texttt {E}}{\sigma _{i}}\right) ^2+ \sum _{i=k+1}^L\left( \frac{\sigma _{i} \texttt {E}}{\lambda ^2}\right) ^2\nonumber \\=\, & \texttt {E}^2\left( \sum _{i=1}^k\sigma _{i}^{-2}+ \lambda ^{-4}\sum _{i=k+1}^L\sigma _{i}^2\right) . \end{aligned}$$

(22)

Here, $\sum _{i=1}^k\sigma _{i}^{-2}$ is roughly equal to $\sigma _{k}^{-2}\,\cong\, \lambda ^{-2}$ whereas $\sum _{i=k+1}^L\sigma _{i}^2$ is roughly equal to $\sigma _{k+1}^2\,\cong\, \lambda ^2$, which gives

$$\begin{aligned} \left\| {{\varvec{x}}}_{\lambda }^e\right\| _{2}\,\cong\, \frac{c_{\lambda } \texttt {E}}{\lambda }, \end{aligned}$$

(23)

where $c_{\lambda }$ is certain value that decline with $\lambda$. For (23), as $\lambda$ tends to infinity, solution norm tends to zero. Contrary, as $\lambda$ tends to zero, solution norm tends to $\left\| {{\varvec{A}}}^T{{\varvec{e}}}\right\| _{2}\,\cong\, \texttt {E}\left\| {{\varvec{A}}}^T\right\| _{\texttt {F}}$. (F stands for the Frobenius norm or the HilbertSchmidt norm.)

Further, the square of a residual norm of the errors is

$$\begin{aligned} \left\| {{\varvec{Ax}}}_{\lambda }^e-{{\varvec{e}}}\right\| _{2}^2\,\cong\, \sum _{i=k}^P\texttt {E}^2=\texttt {E}^2\left( P-k\right) . \end{aligned}$$

(24)

For (24), as $\lambda$ tends to infinity, k tends to zero, thus residual norm tends to $\texttt {E}\sqrt{P}\,\cong\, \left\| {{\varvec{e}}}\right\| _{2}$. Contrary, for small $\lambda$, residual norm fades out.

The conclusion about the trade-off curve for the pure errors ${{\varvec{e}}}$ is that it is mainly a line at $\left\| {{\varvec{Ax}}}_{\lambda }^e-{{\varvec{e}}}\right\| _{2}\,\cong\, \left\| {{\varvec{e}}}\right\| _{2}$, and for small values of $\lambda$, $\left\| {{\varvec{A}}}\bar{{{\varvec{x}}}}_{\lambda }-\bar{{{\varvec{y}}}}\right\| _{2}$ drops towards zero.

Eventually, the over-all trade-off curve which combines the exact undisturbed measurements $\bar{{{\varvec{y}}}}$ and pure errors ${{\varvec{e}}}$, formally donated as $\bar{{{\varvec{y}}}}+{{\varvec{e}}}$, can be considered. In the region where $\lambda$ is small, ${{\varvec{u}}}_{i}^T{{\varvec{e}}}$ terms prevail, so the over-all trade-off curve matches the pure errors trade-off curve. Here, ${{\varvec{x}}}_{\lambda }$ matches ${{\varvec{x}}}_{\lambda }^e$. Otherwise, in the region where $\lambda$ is large, ${{\varvec{u}}}_{i}^T\bar{{{\varvec{y}}}}$ terms prevail, so the over-all trade-off curve matches the exact undisturbed measurements trade-off curve. Here, ${{\varvec{x}}}_{\lambda }$ matches $\bar{{{\varvec{x}}}}_{\lambda }$. The over-all trade-off curve is in fact transition from one line to another. The point where the curve has greatest curvature is a turning point after which it is impossible to achieve additional error suppressing, and the only effect left would be meaningless solution suppressing. So, this turning point is a good indicator to a near-optimal $\lambda$. To make curvature more distinctive, the curve is plotted in logarithmic scale.

1.3 Curvature of the Logarithmic Trade-off Curve

Let quantities $\eta$ and $\rho$ are defined as

$$\begin{aligned} \eta =\left\| {{\varvec{x}}}_{\lambda }\right\| _{2}^2\quad \rho =\left\| {{\varvec{Ax}}}_{\lambda }-{{\varvec{y}}}\right\| _{2}^2, \end{aligned}$$

(25)

and successively

$$\begin{aligned} {\hat{\eta }}=\log \eta \quad {\hat{\rho }}=\log \rho \end{aligned}$$

(26)

The trade-off curve is a diagram of ${\hat{\eta }}/2=\log \left\| {{\varvec{x}}}_{\lambda }\right\| _{2}$ against ${\hat{\rho }}/2=\log \left\| {{\varvec{Ax}}}_{\lambda }-{{\varvec{y}}}\right\| _{2}$, where ${\hat{\eta }}$ and ${\hat{\rho }}$ depend on $\lambda$. Let ${\hat{\eta }}'$, ${\hat{\rho }}'$, ${\hat{\eta }}''$, and ${\hat{\rho }}''$ represent the first and second order derivative functions of ${\hat{\eta }}$ and ${\hat{\rho }}$ with respect to $\lambda$. Regarding this, the curvature $\kappa$ of the parametrically given plane curve, as a function of $\lambda$, is

$$\begin{aligned} \kappa =2\frac{{\hat{\rho }}'{\hat{\eta }}''-{\hat{\rho }}''{\hat{\eta }}'}{\left( \left( {\hat{\rho }}'\right) ^2+\left( {\hat{\eta }}'\right) ^2\right) ^{3/2}}, \end{aligned}$$

(27)

and then, the objective is to find more explicit expression about it, suitable for numerical calculations.

The first order derivative functions of ${\hat{\eta }}$ and ${\hat{\rho }}$ are

$$\begin{aligned} {\hat{\eta }}'=\frac{\eta '}{\eta }\quad \texttt {and}\quad {\hat{\rho }}'=\frac{\rho '}{\rho }. \end{aligned}$$

(28)

Equation (13) gives the dependence of $f_{i}$ on $\sigma _{i}$ and $\lambda$, and it allows to derivate the next two equations:

$$\begin{aligned} \frac{df_{i}^2}{d\lambda }=-\frac{4}{\lambda }\left( 1-f_{i}\right) f_{i}^2\quad \texttt {and}\quad \frac{d\left( 1-f_{i}\right) ^2}{d\lambda }=\frac{4}{\lambda }\left( 1-f_{i}\right) ^2f_{i}. \end{aligned}$$

(29)

Considering (15), (16), (25), and using (29), follows that the first order derivative functions of $\eta$ and $\rho$ are

$$\begin{aligned} \eta '=-\frac{4}{\lambda }\sum _{i=1}^L\left( 1-f_{i}\right) f_{i}^2\frac{\beta _{i}^2}{\sigma _{i}^2}\quad \texttt {and}\quad \rho '=\frac{4}{\lambda }\sum _{i=1}^L\left( 1-f_{i}\right) ^2f_{i}\beta _{i}^2 \end{aligned}$$

(30)

where $\beta _{i}={{\varvec{u}}}_{i}^T{{\varvec{y}}}$.

Relation (13) can be reformulated as

$$\begin{aligned} \frac{f_{i}}{\sigma _{i}}=\frac{1}{\sigma _{i}^2+\lambda ^2}=\frac{1-f_{i}}{\lambda ^2}, \end{aligned}$$

(31)

which in turn gives an important conclusion

$$\begin{aligned} \rho '=-\lambda ^2\eta '. \end{aligned}$$

(32)

The second order derivative functions of ${\hat{\eta }}$ and ${\hat{\rho }}$ are

$$\begin{aligned} {\hat{\eta }}''=\frac{d}{d\lambda }\frac{\eta '}{\eta }=\frac{\eta ''\eta -\left( \eta '\right) ^2}{\eta ^2}\quad \texttt {and}\quad {\hat{\rho ''}}=\frac{d}{d\lambda }\frac{\rho '}{\rho }=\frac{\rho ''\rho -\left( \rho '\right) ^2}{\rho ^2}. \end{aligned}$$

(33)

Respecting (32), the second order derivative function of $\rho$ is

$$\begin{aligned} \rho ''=\frac{d}{d\lambda }\left( -\lambda ^2\eta '\right) =-2\lambda \eta '-\lambda ^2\eta ''. \end{aligned}$$

(34)

With substituting (28) and (33) into (27) and then exploiting (32) and (34), the expression for $\kappa$ gets transformed into

$$\begin{aligned} \kappa =2\frac{\eta \rho }{\eta '}\frac{\lambda ^2\eta '\rho +2\lambda \eta \rho +\lambda ^4\eta \eta '}{\left( \lambda ^2\eta ^2+\rho ^2\right) ^{3/2}}, \end{aligned}$$

(35)

where $\eta '$ is given by (30).