Effects of CEE and Feedback Error on Performance for AF-ORS with PSA-CE Schemes Over Quasi-Static Rayleigh Fading Channels

Abstract

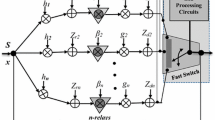
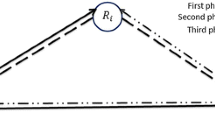
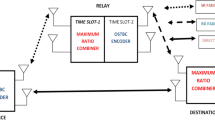
In this paper, we propose the analytical approach for amplify-and-forward (AF) opportunistic relaying schemes (ORS). When operation of AF-ORS consists of relay selection and data transmission phases based on pilot symbol assisted-channel estimation (PSA-CE) methods over quasi-static Rayleigh fading channels, we show that the relay selection phase can be implemented by pilots symbols transmission for source-relay and relay-destination. Moreover, the feedback method for the selected relay index is proposed to have a simple fashion. Then, we investigate the effects of both a channel estimation error and an estimated noise variance, which are obtained by PSA-CE methods, on the received signal-to-noise ratio (SNR). The average SNR loss is also derived in terms with the number of pilots in PSA-CE methods. Moreover, the average symbol error rate, the outage probability, and the normalized channel capacity of the ORS are derived in approximated closed-form expressions for an arbitrary link SNR when the channel state information in the source-relay-destination link is estimated based on transmitted pilots symbols. As the number of pilot symbols, the derived analytical approach is verified, and by comparing it with simulation results, the accuracy is demonstrated. In addition, it is verified that the effect of the feedback error can be neglected for PAS-CE methods over quasi-static fading channels.

Appendices

Appendix 1: Approximated Value of S–R Link’s Estimated Noise Variance

By using the estimated channel coefficient $\hat{h}_{i}$ of (2) and the known pilot symbols $\left\{ s^p|_{p=1}^{N_P} \right\}$, the estimated noise variance for the pilot symbol transmission can be written as Eq. (3) and $y_{i}^p - {\hat{h}_{i}} s^p$ can be presented as

$$\begin{aligned} \begin{aligned} y_{i}^p - {\hat{h}_{i}} s^p&= h_{i} \sqrt{E_i} s^p + n_{i}^p - {\hat{h}_{i}} s^p = \left[ \hat{h}_{i} - e_{i} \right] s^p + n_{i}^p - {\hat{h}_{i}} s^p \\&= - e_{i} s^p + n_{i}^p = - \frac{1}{N_P}\sum _{k=1, k \ne p}^{N_P} {s^{k}}^* s^p n_{i}^k + \frac{N_P -1}{N_P} n_{i}^p \end{aligned} \end{aligned}$$

(53)

with $\hat{h}_{i} = \frac{1}{N_P}\sum _{p=1}^{N_P} {s^{p}}^* y_{i}^p = h_{i} \sqrt{E_i} + e_{i}$ and $e_{i} = \frac{1}{N_P}\sum _{p=1}^{N_P} {s^{p}}^* n_{i}^p$. Note that (53) has $N_P$ independent AWGN terms $\left\{ n_{i}^{p}|_{p=1}^{N_P} \right\}$. Therefore, it leads to

$$\begin{aligned} \begin{aligned} \sigma _{P,i}^{2} = E\left[ \left| y_{i}^p - {\hat{h}_{i}} s^p \right| ^2 \right]&= E\left[ \left| - e_{i} s^p + n_{i}^p \right| ^2 \right] \\&= \frac{N_P-1}{N_P^2} \sigma ^2 + \frac{(N_P-1)^2}{N_P^2} \sigma ^2 = \frac{N_P-1}{N_P} \sigma ^2 \end{aligned} \end{aligned}$$

(54)

with $E\left[ n_{i}^p \right] =0$ and $E\left[ |n_{i}^p|^2 \right] =\sigma ^2$ for $p\in \{1,2,\ldots ,N_P\}$. Note that $\sigma _{P,i}^{2}$ of (54) is used for the approximated value of ${\hat{\sigma }}_{P,i}^{2}$ in (3).

Appendix 2: Approximated Value of R–D Link’s Estimated Noise Variance

From (5), (6), and (7), the channel estimation error of the ith indirect link can be represented as

$$\begin{aligned} \begin{aligned} e_{L+i}&= \frac{1}{N_P}\sum _{p=1}^{N_P} {s^{p}}^* {n_{L+i}^p}^{'} \\&= \frac{1}{N_P}\sum _{p=1}^{N_P} {s^{p}}^* \left[ \frac{h_{L+i}\sqrt{E_{L+i}^{}}}{|\hat{h}_{i}|}(-e_{i}s^p+n_{i}^p)+n_{L+i}^p \right] \\&= \frac{h_{L+i}\sqrt{E_{L+i}^{}}}{|\hat{h}_{i}|} \left[ -e_{i} \frac{1}{N_P} \sum _{p=1}^{N_P} {s^{p}}^* s^p + \frac{1}{N_P} \sum _{p=1}^{N_P} {s^{p}}^* n_{i}^p \right] + \frac{1}{N_P}\sum _{p=1}^{N_P} {s^{p}}^* n_{L+i}^p \\&= \frac{1}{N_P}\sum _{p=1}^{N_P} {s^{p}}^* n_{L+i}^p \end{aligned} \end{aligned}$$

(55)

with $\frac{1}{N_P} \sum _{p=1}^{N_P} |s^p|^2 = 1$ and $e_{i} = \frac{1}{N_P}\sum _{p=1}^{N_P} {s^{p}}^* n_{i}^p$. In $e_{L+i}=\frac{1}{N_P}\sum _{p=1}^{N_P} {s^{p}}^* n_{L+i}^p$, the CEE term related with S–R link (i.e., $e_{i}$) is eliminated and then, $e_{L+i}$ is only related with R–D link’s noise terms $\left\{ n_{L+i}^p|_{p=1}^{N_P} \right\}$. Therefore, we can easily obtain $E[e_{L+i} ]=0$ and $E[|e_{L+i}|^2]=\sigma ^2 / N_P$.

From (5), (6), and (7), we can obtain

$$\begin{aligned} \begin{aligned} {n_{L+i}^{p}}{'}&=\frac{h_{L+i}\sqrt{E_{L+i}^{}}}{|\hat{h}_{i}|}(-e_{i}s^p+n_{i}^p)+n_{L+i}^p\\&=\frac{\hat{h}_{L+i} - e_{L+i}}{\hat{h}_{i}}(-e_{i}s^p+n_{i}^p)+n_{L+i}^p \end{aligned} \end{aligned}$$

and then, $y_{L+i}^p$ is represented as

$$\begin{aligned} \begin{aligned} y_{L+i}^p&= h_{L+i} G_i y_{i}^p + n_{L+i}^p \\&=h_{L+i}^{'}s^p + {n_{L+i}^{p}}{'} \\&= \left( \hat{h}_{L+i} - e_{L+i}\right) s^p + \frac{\hat{h}_{L+i} - e_{L+i}}{|\hat{h}_{i}|} \left( - e_{i}s^p + n_{i}^p \right) + n_{L+i}^p. \end{aligned} \end{aligned}$$

(56)

with $y_{i}^p = h_{i} \sqrt{E_i} s^p + n_{i}^p$, $G_{i} = \frac{\sqrt{E_{L+i}^{}}}{|\hat{h}_{i}|}$, $\hat{h}_{i} = h_{i} \sqrt{E_i} + e_{i}$, $\hat{h}_{L+i} = h_{L+i}^{'} + e_{L+i}$, $e_{i} = \frac{1}{N_P}\sum _{p=1}^{N_P} {s^{p}}^* n_{i}^p$, and $e_{L+i} = \frac{1}{N_P}\sum _{p=1}^{N_P} {s^{p}}^* n_{L+i}^p$. From (56), $y_{L+i}^p - {\hat{h}_{L+i}} s^p$ in (8) can be expressed as

$$\begin{aligned} \begin{aligned} y_{L+i}^p - {\hat{h}_{L+i}} s^p&= \left[ \hat{h}_{L+i} - e_{L+i} \right] s^p + {n_{L+i}^{p}}{'} - {\hat{h}_{L+i}} s^p \\&= - e_{L+i} s^p + {n_{L+i}^{p}}{'} \\&= \left( - e_{L+i} s^p + n_{L+i}^p \right) + \frac{\hat{h}_{L+i} - e_{L+i}}{\hat{h}_{i}} \left( -e_{i}s^p+n_{i}^p \right) \end{aligned} \end{aligned}$$

(57)

where both $\left( - e_{L+i} s^p + n_{L+i}^p \right)$ and $\left( -e_{i}s^p+n_{i}^p \right)$ are independent and have $N_P$ independent AWGN terms of $\left\{ n_{L+i}^{p}|_{p=1}^{N_P} \right\}$ and $\left\{ n_{i}^{p}|_{p=1}^{N_P} \right\}$, respectively. Similar with (54), we can obtain

$$\begin{aligned} \begin{aligned} E\left[ \left| - e_{L+i} s^p + n_{L+i}^p \right| ^2 \right] = \frac{N_P-1}{N_P} \sigma ^2. \end{aligned} \end{aligned}$$

(58)

Consequently, for the given $\hat{h}_{i}$ and $\hat{h}_{L+i}$, it leads to

$$\begin{aligned} \begin{aligned} \sigma _{P,L+i}^2&= E\left[ \left| y_{L+i}^p - {\hat{h}_{L+i}} s^p \right| ^2 \right] \\&= E\left[ \left| - e_{L+i} s^p + {n_{L+i}^{p}}{'} \right| ^2 \right] \\&= \left( 1+\frac{ |\hat{h}_{L+i} |^2 + {\sigma ^2}/{N_P} }{|\hat{h_{i}}|^2}\right) \frac{N_P-1}{N_P} \sigma ^2 \end{aligned} \end{aligned}$$

(59)

with

$$\begin{aligned} \begin{aligned} E\left[ | \hat{h}_{L+i} - e_{L+i} |^2 \right] = |\hat{h}_{L+i}|^2 + E\left[ |e_{L+i}|^2 \right] = |\hat{h}_{L+i}|^2 + \frac{\sigma ^2}{N_P}. \end{aligned} \end{aligned}$$

Note that $\sigma _{P,L+i}^{2}$ of (59) is used for the approximated value of ${\hat{\sigma }}_{P,i}^{2}$ in (8).

Appendix 3: Derivation of ${\bar{\gamma }}_{\text {AF}_i}$

By letting $z=\frac{xy}{x+y}$, (36) can be rewritten as

$$\begin{aligned} \begin{aligned} {\bar{\gamma }}_{\text {AF}_i}&= \int _{0}^{\infty } z \int _{z}^{\infty } \frac{y^2}{(y-z)^2} \frac{1}{{\bar{\gamma }}_{ i}} e^{ -\frac{yz/(y-z)}{{\bar{\gamma }}_{i}} } \frac{1}{{\bar{\gamma }}_{L+i}} e^{ -\frac{y }{{\bar{\gamma }}_{L+i}} } dy dz \\&= \int _{0}^{\infty } z f_{z} (z) dz. \end{aligned} \end{aligned}$$

(60)

Note that the lower limit of the integral related with y comes to the fact that the random variable of y is always greater than or equal to z (since $x=yz/(y-z)$ must to be greater than or equal to 0, it is easy to see $y \ge z$) [10, 32]. Furthermore, the inner integral term in (60) can be regarded as the PDF of z and expressed as

$$\begin{aligned} \begin{aligned} f_{z} (z)&= \frac{1}{{\bar{\gamma }}_{i}{\bar{\gamma }}_{L+i}} \int _{z}^{\infty } \frac{y^2}{(y-z)^2} e^{ -\frac{yz}{{\bar{\gamma }}_{i}(y-z)} } e^{ -\frac{y}{{\bar{\gamma }}_{L+i}} } dy \\&= \frac{1}{{\bar{\gamma }}_{i}{\bar{\gamma }}_{L+i}} \int _{0}^{1} \frac{z}{t^2(1-t)^2} \exp \left( -\frac{z}{{\bar{\gamma }}_{i}(1-t)} -\frac{z}{{\bar{\gamma }}_{L+i} t} \right) dt \end{aligned} \end{aligned}$$

(61)

with $t=z/y$. Then, changing the order if the integrals of z and t, we can have

$$\begin{aligned} \begin{aligned} {\bar{\gamma }}_{\text {AF}_i}&= \frac{1}{{\bar{\gamma }}_{i}{\bar{\gamma }}_{L+i}} \int _{0}^{1} \frac{1}{t^2(1-t)^2} \left[ \int _{0}^{\infty } z^2 \exp \left( -\left( \frac{1}{{\bar{\gamma }}_{i}(1-t)} +\frac{1}{{\bar{\gamma }}_{L+i} t} \right) z \right) dz \right] dt \\&= \frac{1}{{\bar{\gamma }}_{i}{\bar{\gamma }}_{L+i}} \int _{0}^{1} \frac{2}{t^2(1-t)^2 A^3} dt \\&= 2\left( {\bar{\gamma }}_{i}{\bar{\gamma }}_{L+i}\right) ^2 \int _{0}^{1} \frac{t(1-t)}{ (a+bt)^3 } dt \end{aligned} \end{aligned}$$

(62)

with $\int _{0}^{\infty } z^2 e^{-Az} dz = 2A^{-3}$, ${A}^{-1} = \frac{ {\bar{\gamma }}_{i}{\bar{\gamma }}_{L+i}t(1-t) }{{\bar{\gamma }}_{i} + ({\bar{\gamma }}_{L+i}-{\bar{\gamma }}_{i})t}$, $a={\bar{\gamma }}_{i}$, and $b={\bar{\gamma }}_{L+i}-{\bar{\gamma }}_{i}$. Finally, it produces

$$\begin{aligned} \begin{aligned} \int _{0}^{1} \frac{t(1-t)}{ (a+bt)^3 } dt = {\left\{ \begin{array}{ll} \frac{(2a+b)}{2a(a+b)b^2} + \frac{1}{b^3} \ln \frac{a}{a+b} & \quad {\text {if}}\,\, b \ne 0 \\ \frac{1}{6a^3} & \quad {\text {else}} \end{array}\right. } \end{aligned} \end{aligned}$$

(63)

and from (62) and (63), we can obtain ${\bar{\gamma }}_{\text {AF}_i}$ as (37).