Iterative Self-Interference Mitigation in Full-Duplex Wireless Communications

Abstract

This paper considers a full-duplex wireless communication system in which detection of the desired signal is hindered not only by the self-interference (SI), but also phase noise, in-phase and quadrature-phase imbalance and power amplifier’s nonlinearity distortion. An iterative algorithm is proposed in which the processes of SI cancellation and detection of the desired signal aid each other in each iteration. In each iteration, the SI cancellation process performs widely linear estimation of the SI channel and compensates for physical impairments to improve the detection performance of the desired signal. The detected desired signal is in turn removed from the received signal to improve SI channel estimation and SI cancellation in the next iteration. Simulation results show that the proposed algorithm significantly outperforms existing algorithms in SI cancellation and detection of the desired signal.

Appendices

Appendices

1.1 Derivation of Eq. (2)

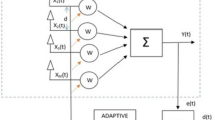
Refering to Fig. 1, after DAC, the signal w(t) is up-converted to a carrier frequency $f_c$ with quadrature mixers. In the perfect matching case between the I and Q branches, the output of the LO would be

$$\begin{aligned} z_p(t)=\sqrt{2}w_I(t)\cos {\left( 2\pi f_c t\right) }-\sqrt{2}w_Q(t)\sin {\left( 2\pi f_c t\right) } \end{aligned}$$

(29)

However, the LO is not ideal in practice which results in phase noise and IQ imbalance impairments. Denoting by $\alpha _T$, $\theta _T$ and $\phi _T(t)$ the gain, phase imbalance related to the IQ imbalance impairment and phase offset related to the phase noise impairment, respectively. In practice, $\alpha _T$ and $\theta _T$ are static paremeters, while $\phi _T(t)$ is changing in time. Thus, the output of the LO can be represented as

$$\begin{aligned} \begin{aligned} z_p(t)=&\sqrt{2}(1+\alpha _T)w_I(t)\cos {\left( 2\pi f_c t+\frac{\theta _T}{2}+\phi _T(t)\right) }\\&-\sqrt{2}(1-\alpha _T)w_Q(t)\sin {\left( 2\pi f_c t-\frac{\theta _T}{2}+\phi _T(t)\right) }\\ \end{aligned} \end{aligned}$$

(30)

The expression in (30) can be expanded as in (31)

$$\begin{aligned} \begin{aligned} z_p(t)=&\sqrt{2}(1+\alpha _T)w_I(t)\left( \frac{{{\mathrm {e}}}^{j\left( 2\pi f_ct+\frac{\theta _T}{2}+\phi _T(t)\right) }+{{\mathrm {e}}}^{-j\left( 2\pi f_ct+\frac{\theta _T}{2}+\phi _T(t)\right) }}{2}\right) \\&-\sqrt{2}(1-\alpha _T)w_Q(t)\left( \frac{{{\mathrm {e}}}^{j\left( 2\pi f_ct-\frac{\theta _T}{2}+\phi _T(t)\right) }-{{\mathrm {e}}}^{-j\left( 2\pi f_ct-\frac{\theta _T}{2}+\phi _T(t)\right) }}{2j}\right) \\ =&\sqrt{2}{{\mathrm {e}}}^{j(2\pi f_ct+\phi _T(t))}\left( (1+\alpha _T)w_I(t)\frac{{{\mathrm {e}}}^{j\frac{\theta _T }{2}}}{2}-(1-\alpha _T)w_Q(t)\frac{{{\mathrm {e}}}^{-j\frac{\theta _T}{2}}}{2j}\right) \\&+\sqrt{2}{{\mathrm {e}}}^{-j(2\pi f_ct+\phi _T(t))}\left( (1+\alpha _T)w_I(t)\frac{{{\mathrm {e}}}^{-j\frac{\theta _T}{2}}}{2}+(1-\alpha _T)w_Q(t)\frac{{{\mathrm {e}}}^{j\frac{\theta _T}{2}}}{2j}\right) \\ =&\frac{1}{\sqrt{2}}{{\mathrm {e}}}^{j(2\pi f_ct+\phi _T(t))}\underbrace{\left( (1+\alpha _T)w_I(t){{\mathrm {e}}}^{j\frac{\theta _T }{2}}+j(1-\alpha _T)w_Q(t){{\mathrm {e}}}^{-j\frac{\theta _T}{2}}\right) }_{I_1}\\&+\frac{1}{\sqrt{2}}{{\mathrm {e}}}^{-j(2\pi f_ct+\phi _T(t))}\underbrace{\left( (1+\alpha _T)w_I(t){{\mathrm {e}}}^{-j\frac{\theta _T}{2}}-j(1-\alpha _T)w_Q(t){{\mathrm {e}}}^{j\frac{\theta _T}{2}}\right) }_{I_2}\\ \end{aligned} \end{aligned}$$

(31)

The term $I_1$ can be rewritten as

$$\begin{aligned} \begin{aligned} I_1=&(1+\alpha _T)w_I(t){{\mathrm {e}}}^{j\frac{\theta _T }{2}}+j(1-\alpha _T)w_Q(t){{\mathrm {e}}}^{-j\frac{\theta _T}{2}}\\& =\left( 1+\alpha _T\right) \frac{w(t)+w^*(t)}{2}\left( \cos \frac{\theta _T}{2}+j\sin \frac{\theta _T}{2}\right) \\&+ j\left( 1-\alpha _T\right) \frac{w(t)-w^*(t)}{2j}\left( \cos \frac{\theta _T}{2}-j\sin \frac{\theta _T}{2}\right) \\ &=\left( \cos \frac{\theta _T}{2}+j\alpha _T\sin \frac{\theta _T}{2}\right) w(t)\\&+\left( \alpha _T\cos \frac{\theta _T}{2}+j\sin \frac{\theta _T}{2}\right) w^*(t) \end{aligned} \end{aligned}$$

(32)

Define

$$\begin{aligned} \begin{aligned} \xi _T&=\cos \frac{\theta _T}{2}+j\alpha _T\sin \frac{\theta _T}{2}\\ \eta _T&=\alpha _T\cos \frac{\theta _T}{2}+j\sin \frac{\theta _T}{2} \end{aligned} \end{aligned}$$

(33)

Then

$$\begin{aligned} I_1=\xi _T w(t) + \eta _T w^{*}(t). \end{aligned}$$

(34)

A similar expression can be obtained for $I_2$ and it is simple to show that

$$\begin{aligned} I_2 = I_1^* \end{aligned}$$

(35)

Finally,

$$\begin{aligned} \begin{aligned} z_p(t) =&\frac{1}{\sqrt{2}}{{\mathrm {e}}}^{j2\pi f_ct}\left[ {{\mathrm {e}}}^{j\phi _T(t)}\left( \xi _T w(t) + \eta _T w^{*}(t)\right) \right] \\&+\frac{1}{\sqrt{2}}{{\mathrm {e}}}^{-j2\pi f_ct}\left[ {{\mathrm {e}}}^{j\phi _T(t)}\left( \xi _T w(t) + \eta _T w^{*}(t)\right) \right] ^{*}\\ =&\sqrt{2}\mathfrak {R}\left\{ {{\mathrm {e}}}^{j\phi _T(t)}\left( \xi _T w(t) + \eta _T w^{*}(t)\right) {{\mathrm {e}}}^{j2\pi f_ct}\right\} \\ =&\sqrt{2}\mathfrak {R}\left\{ z(t){{\mathrm {e}}}^{j2\pi f_c t}\right\} \end{aligned} \end{aligned}$$

(36)

The above expression means that the complex baseband equivalent signal of $z_p(t)$ is $z(t)={{\mathrm {e}}}^{j\phi _T(t)}\left( \xi _T w(t) + \eta _T w^{*}(t)\right)$.

1.2 Derivation of Eq. (16)

From (1), (2), and (8) one obtains

$$\begin{aligned} \begin{aligned} u(t) =\,&\alpha {\mathrm {e}}^{j\phi _T(t)}\left( \xi _T w(t)+\eta _Tw^*(t)\right) + d(t)\\ {\mathop {=}\limits ^{(1)}}\,&\alpha {\mathrm {e}}^{j\phi _T(t)}\left( \xi _T \sum \limits _{l=0}^{N-1}x(l)q(t-lT_s)\right. \\&\quad +\left. \eta _T \sum \limits _{l=0}^{N-1}x^*(l)q(t-lT_s)\right) + d(t)\\ \end{aligned} \end{aligned}$$

(37)

Thus

$$\begin{aligned} \begin{aligned} u(kT_s) =\,&u(t)\biggr |_{t=kT_s}\\ =\,&\alpha {\mathrm {e}}^{j\phi _T(kT_s)}\left( \xi _T \sum \limits _{l=0}^{N-1}x(l)q(kT_s-lT_s)\right. \\&\quad +\left. \eta _T \sum \limits _{l=0}^{N-1}x^*(l)q(kT_s-lT_s)\right) + d(kT_s)\\ \end{aligned} \end{aligned}$$

(38)

Dropping $T_s$ in (38) results in

$$\begin{aligned} \begin{aligned} u(k)&=\alpha {\mathrm {e}}^{j\phi _T(k)}\left( \xi _T \sum \limits _{l=0}^{N-1}x(l){\tilde{q}}(k-l)+\eta _T \sum \limits _{l=0}^{N-1}x^*(l)\tilde{q}(k-l)\right) + d(k)\\ \end{aligned} \end{aligned}$$

(39)

in which $\tilde{q}(n)$ is obtained by downsampling q(n) with factor F, $n = 0,\ldots ,M-1$.

From (39), $y_1(k)$ is written as (40)

$$\begin{aligned} \begin{aligned} y_1(k)=\,&h(k)*\left( \alpha {\mathrm {e}}^{j\phi _T(k)}\left( \xi _T \sum \limits _{l=0}^{N-1}x(l)\tilde{q}(k-l)+\eta _T \sum \limits _{l=0}^{N-1}x^*(l)\tilde{q}(k-l)\right) + d(k)\right) \\ =\,&\alpha \xi _T h(k)*\left( {\mathrm {e}}^{j\phi _T(k)} \sum \limits _{l=0}^{N-1}x(l)\tilde{q}(k-l)\right) \\&+\alpha \eta _T h(k)*\left( {\mathrm {e}}^{j\phi _T(k)}\sum \limits _{l=0}^{N-1}x^*(l)\tilde{q}(k-l)\right) + h(k)*d(k)\\ =\,&\alpha \xi _T \sum \limits _{i=0}^{N-1}\left( {\mathrm {e}}^{j\phi _T(i)} \sum \limits _{l=0}^{N-1}x(l)\tilde{q}(i-l)\right) h(k-i)\\&+\alpha \eta _T \sum \limits _{i=0}^{N-1}\left( {\mathrm {e}}^{j\phi _T(i)}\sum \limits _{l=0}^{N-1}x^*(l)\tilde{q}(i-l)\right) h(k-i) + h(k)*d(k)\\ \end{aligned} \end{aligned}$$

(40)

With the definition of matrices ${\mathbf {Q}}$, ${\mathbf {H}}$ and ${\mathbf {P}}_T$ in Sect. 2, (40) is rewritten compactly as

$$\begin{aligned} {\mathbf {y}}_1 = \alpha \xi _T {\mathbf {H}}{\mathbf {P}}_T{\mathbf {Q}}{\mathbf {x}} + \alpha \eta _T {\mathbf {H}}{\mathbf {P}}_T{\mathbf {Q}}{\mathbf {x}}^{*} \end{aligned}$$

(41)

where ${\mathbf {y}}_1 = \begin{bmatrix} y_1(0)&y_1(1)&\cdots&y_1(N-1) \end{bmatrix}^T$. Similarly, $y_2(k)$ can be compactly written as ${\mathbf {y}}_2 = {\mathbf {G}}{\mathbf {Q}}{\mathbf {c}}$, where ${\mathbf {G}}$ and ${\mathbf {c}}$ are defined as in Sect. 2.