Performance Analysis of Satellite-Terrestrial Network of Weibull Fading Channel

Abstract

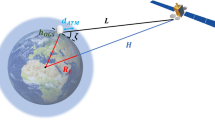
Unlike Rayleigh or Nakagami-m fading which has been widely studied in hybrid satellite-terrestrial relay network, the multi-branch Weibull fading which can be an alternative has been less studied due to its high intractability. In the proposed satellite-terrestrial Weibull system, by applying multi-branch optimal transmitting beamforming/receiving combination strategy, an upper bound of signal to noise (SNR) based outage probability (OP) is analyzed compared with the exact OP. Besides, two different methods are used to calculate the intractable Ergodic Capacity. Moreover, the closed-form expressions of the average symbol error rate (ASER) and Effective Capacity are hard to derive. Hence, simplified theoretical results of ASER and Effective Capacity are presented via the proposed upper bound of SNR scheme. Finally, various parameters are verified to illustrate the performance of the proposed model and demonstrate the effectiveness of our method.

Appendices

Appendix A

As is depicted in Eq. (7), $I_1$ is derived as

$$\begin{aligned} {I_1} = \int _0^\infty {\frac{{{{\left( {x + {r_{th}} + 1} \right) }^p}{{\left( {x + {r_{th}}} \right) }^{\varPhi - 1}}}}{{{x^p}}}\exp \left( { - \frac{{\left( {\beta - \delta } \right) {r_{th}}\left( {{r_{th}} + 1} \right) }}{{{c_{sr}}{{{{\bar{\gamma }}} }_s}x}} - \varPsi x} \right) } dx, \end{aligned}$$

(43)

With the help of polynomial expansion Eq.(1.111) in [20], then we make use of the transformation of Meijer’s G-function in Eq.(07.34.03.0046.01) in [22] and Eq. (10) in [19], the integral operation can be solved by Eq. (3.1) in [21]. The closed form of $I_1$ is shown as:

$$\begin{aligned} \begin{array}{l} {I_1} = \sum \limits _{l = 0}^p {\left( {\begin{array}{*{20}{c}} p\\ l \end{array}} \right) \int _0^\infty {{x^{ - p}}{{\left( {x + {r_{th}}} \right) }^{l + \varPhi - 1}}\exp \left( { - \frac{{\left( {\beta - \delta } \right) {r_{th}}\left( {{r_{th}} + 1} \right) }}{{{c_{sr}}{{{{\bar{\gamma }}} }_s}x}}} \right) } \exp \left( { - \varPsi x} \right) dx} \\ \quad = \sum \limits _{l = 0}^p {\left( {\begin{array}{*{20}{c}} p\\ l \end{array}} \right) \frac{{{b^{a - 1}}{r_{th}}^{l + \varPhi - 1}}}{{\varGamma \left( { - c} \right) }}} {\varPsi ^{ - 1}}\mathop G\nolimits _{1,[1:1],0,[0:1]}^{1,1,1,0,1} \left( {\begin{array}{*{20}{c}} {\frac{1}{{b\varPsi }}}\\ {\frac{1}{{{r_{th}}\varPsi }}} \end{array}\left| {\begin{array}{*{20}{c}} 0\\ {1 - a, - c}\\ - \\ { - ,0} \end{array}} \right. } \right) \end{array}. \end{aligned}$$

(44)

where b denotes ${{\left[ {\left( {\beta - \delta } \right) {r_{th}}\left( {{r_{th}} + 1} \right) } \right] } \big / {\left( {{c_{sr}}{{{{\bar{\gamma }}} }_s}} \right) }}$, a represents $1-p$, c is $l + \varPhi - 1$.

Finally, by substituting Eq. (44) into Eq. (11) and with several mathematical simplification, we get the expression of Outage Probability given in Eq. (12).

Appendix B

By substituting Eq. (24) into Eq. (23), ${{{\bar{C}}}_3}$ can be transformed as

$$\begin{aligned} {{{{\bar{C}}}}_3} &= - \sum \limits _{{k_1} = 0}^{{m_s} - 1} { \cdots \sum \limits _{{k_M} = 0}^{{m_s} - 1} {\frac{{\varXi \left( M \right) \varLambda !{\varPsi ^\varPhi }}}{{c_{sr}^\varLambda {{\bar{\gamma }}} _s^\varLambda }}} } \underbrace{\int _0^\infty {\frac{{{E_1}\left( { - s} \right) }}{{{{\left( {s + \varPsi } \right) }^\varPhi }{{\left( {\frac{{\beta - \delta }}{{{c_{sr}}{{{{\bar{\gamma }}} }_s}}} + s} \right) }^{\varLambda + 1}}}}ds} }_{{I_2}}\\ &\quad - \sum \limits _{{k_1} = 0}^{{m_s} - 1} { \cdots \sum \limits _{{k_M} = 0}^{{m_s} - 1} {\frac{{\varXi \left( M \right) \varGamma \left( \varLambda \right) {\varPsi ^\varPhi }\varPhi }}{{c_{sr}^\varLambda {{\bar{\gamma }}} _s^\varLambda }}} } \underbrace{\int _0^\infty {\frac{{{E_1}\left( { - s} \right) }}{{{{\left( {\frac{{\beta - \delta }}{{{c_{sr}}{{{{\bar{\gamma }}} }_s}}} + s} \right) }^\varLambda }{{\left( {s + \varPsi } \right) }^{\varPhi + 1}}}}ds} }_{{I_3}} , \end{aligned}$$

(45)

With the aid of Eq. (10) in [19] and Eq. (3.1) in [21], we can obtain the results of $I_2$, $I_3$ given as follows:

$$\begin{aligned}&\begin{array}{l} {I_2} = \frac{{{\varPsi ^{ - \varPhi }}{{\left( {\frac{{\beta - \delta }}{{{{{{\bar{\gamma }}} }_s}}}} \right) }^{ - \varLambda - 1}}}}{{\varGamma \left( \varPhi \right) \varGamma \left( {\varLambda + 1} \right) }}\int _0^\infty {\mathop G\nolimits _{1,1}^{1,1} \left( {\frac{s}{\varPsi }\left| {\begin{array}{*{20}{c}} {1 - \varPhi }\\ 0 \end{array}} \right. } \right) \mathop G\nolimits _{1,1}^{1,1} \left( {\frac{{{c_{sr}}{{{{\bar{\gamma }}} }_s}s}}{{\beta - \delta }}\left| {\begin{array}{*{20}{c}} { - \varLambda }\\ 0 \end{array}} \right. } \right) \mathop G\nolimits _{1,2}^{2,0} \left( {s\left| {\begin{array}{*{20}{c}} 1\\ {0,0} \end{array}} \right. } \right) ds} \\ \quad = \frac{{{\varPsi ^{ - \varPhi }}{{\left( {\frac{{\beta - \delta }}{{{c_{sr}}{{{{\bar{\gamma }}} }_s}}}} \right) }^{ - \varLambda - 1}}}}{{\varGamma \left( \varPhi \right) \varGamma \left( {\varLambda + 1} \right) }}\mathop G\nolimits _{2,[1,1],1,[1,1]}^{2,1,1,1,1} \left( {\begin{array}{*{20}{c}} {\frac{1}{\varPsi }}\\ {\frac{{{c_{sr}}{{{{\bar{\gamma }}} }_s}}}{{\beta - \delta }}} \end{array}\left| {\begin{array}{*{20}{c}} {0,0}\\ {\varPhi ;1 + \varLambda }\\ 2\\ {0;0} \end{array}} \right. } \right) \end{array}, \end{aligned}$$

(46)

$$\begin{aligned}&\begin{array}{l} {I_3} = \frac{{{{\left( {\frac{{\beta - \delta }}{{{c_{sr}}{{{{\bar{\gamma }}} }_s}}}} \right) }^{ - \varLambda }}{\varPsi ^{ - \varPhi - 1}}}}{{\varGamma \left( \varLambda \right) \varGamma \left( {\varPhi + 1} \right) }}\int _0^\infty {\mathop G\nolimits _{1,1}^{1,1} \left( {\frac{s}{\varPsi }\left| {\begin{array}{*{20}{c}} { - \varPhi }\\ 0 \end{array}} \right. } \right) \mathop G\nolimits _{1,1}^{1,1} \left( {\frac{{{c_{sr}}{{{{\bar{\gamma }}} }_s}s}}{{\beta - \delta }}\left| {\begin{array}{*{20}{c}} {1 - \varLambda }\\ 0 \end{array}} \right. } \right) \mathop G\nolimits _{1,2}^{2,0} \left( {s\left| {\begin{array}{*{20}{c}} 1\\ {0,0} \end{array}} \right. } \right) ds} \\ \quad = \frac{{{{\left( {\frac{{\beta - \delta }}{{{c_{sr}}{{{{\bar{\gamma }}} }_s}}}} \right) }^{ - \varLambda }}{\varPsi ^{ - \varPhi - 1}}}}{{\varGamma \left( \varLambda \right) \varGamma \left( {\varPhi + 1} \right) }}\mathop G\nolimits _{2,[1,1],1,[1,1]}^{2,1,1,1,1} \left( {\begin{array}{*{20}{c}} {\frac{1}{\varPsi }}\\ {\frac{{{c_{sr}}{{{{\bar{\gamma }}} }_s}}}{{\beta - \delta }}} \end{array}\left| {\begin{array}{*{20}{c}} {0,0}\\ {1 + \varPhi ;\varLambda }\\ 2\\ {0;0} \end{array}} \right. } \right) \end{array}. \end{aligned}$$

(47)

Finally, by substituting the calculation results into Eq. (45) and with several mathematical manipulations, the last term of ${{\bar{C}}}$ is shown as Eq. (24).

Appendix C

As is shown in Eq. (38), we can know that MGF is needed to calculate the Effective Capacity. However, the third term in Eq. (32) cannot be used for calculating directly.Herein, we provide an alternative method based on the approximate instead. Substituting Eq. (13) into Eq. (31), where $\exp \left[ { - \left( {s + \frac{{\beta - \delta }}{{{{{{\bar{\gamma }}} }_s}}}} \right) x} \right]$ can be approximated by $\sum \limits _{l = 0}^L {\frac{{{{\left[ { - \left( {s + \frac{{\beta - \delta }}{{{{{{\bar{\gamma }}} }_s}}}} \right) } \right] }^l}}}{{l!}}} {x^l}$ at the time ${{{\bar{\gamma }}} _s}$ goes to infinity, thus the novel MGF can be given as

$$\begin{aligned} {M_r}\left( s \right) &= 1 - s\sum \limits _{{i_1}, \cdots ,{i_M},p} {{\varphi _{{i_1}, \cdots ,{i_M},p}}\frac{{\varGamma \left( {p + 1} \right) }}{{{{\left( {\frac{{\beta - \delta }}{{{c_{sr}}{{{{\bar{\gamma }}} }_s}}} + s} \right) }^{p + 1}}}}} \\ &\quad - s\sum \limits _{{i_1}, \cdots ,{i_M},p} {\frac{{{\varphi _{{i_1}, \cdots ,{i_M},p}}}}{{\varGamma \left( \varPhi \right) }}\sum \limits _{l = 0}^L {\frac{{{{\left( { - \frac{{\beta - \delta }}{{{c_{sr}}{{{{\bar{\gamma }}} }_s}}}} \right) }^l}}}{{l!}}} } {s^{ - p - l - 1}}\mathop G\nolimits _{2,2}^{1,2} \left( {\frac{\varPsi }{s}\left| {\begin{array}{*{20}{c}} { - p - l,1}\\ {\varPhi ,0} \end{array}} \right. } \right) . \end{aligned}$$

(48)

where $\sum \limits _{{i_1}, \cdots ,{i_M},p} {{\varphi _{{i_1}, \cdots ,{i_M},p}}} = \sum \limits _{{i_1} = 0}^{{m_s} - 1} { \cdots \sum \limits _{{i_M} = 0}^{{m_s} - 1} {\frac{{\varXi \left( M \right) }}{{c_{sr}^\varLambda {{\bar{\gamma }}} _s^\varLambda }}\sum \limits _{p = 0}^{\varLambda - 1} {\frac{{\varGamma \left( \varLambda \right) }}{{p!}}} {{\left( {\frac{{\beta - \delta }}{{{c_{sr}}{{{{\bar{\gamma }}} }_s}}}} \right) }^{ - \left( {\varLambda - p} \right) }}} }$.