Skip to main content
SpringerLink
Log in

Codimension-two bifurcations analysis and tracking control on a discrete epidemic model

  • Published:
Journal of Systems Science and Complexity Aims and scope Submit manuscript

Abstract

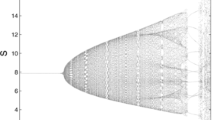
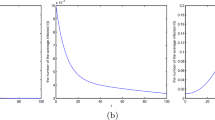
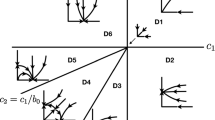
In this paper, the dynamic behaviors of a discrete epidemic model with a nonlinear incidence rate obtained by Euler method are discussed, which can exhibit the periodic motions and chaotic behaviors under the suitable system parameter conditions. Codimension-two bifurcations of the discrete epidemic model, associated with 1:1 strong resonance, 1:2 strong resonance, 1:3 strong resonance and 1:4 strong resonance, are analyzed by using the bifurcation theorem and the normal form method of maps. Moreover, in order to eliminate the chaotic behavior of the discrete epidemic model, a tracking controller is designed such that the disease disappears gradually. Finally, numerical simulations are obtained by the phase portraits, the maximum Lyapunov exponents diagrams for two different varying parameters in 3-dimension space, the bifurcation diagrams, the computations of Lyapunov exponents and the dynamic response. They not only illustrate the validity of the proposed results, but also display the interesting and complex dynamical behaviors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. Satsuma, R. Willox, A. Ramani, et al., Extending the SIR epidemic model, Physica A, 2004, 336(3–4): 369–375.

    Article  Google Scholar 

  2. M. E. Alexander and S. M. Moghadas, Periodicity in an epidemic model with a generalized nonlinear incidence, Mathematical Biosciences, 2004, 189(1): 75–96.

    Article  MATH  MathSciNet  Google Scholar 

  3. H. L. Liu, J. Y. Yu, and G. T. Zhu, Global asymptotic stable eradication for the SIV epidemic model with impulsive vaccination and infection-age, Journal of Systems Science & Complexity, 2006, 19(3): 393–402.

    Article  MATH  MathSciNet  Google Scholar 

  4. C. C. Chavez and A. A. Yakubu, Dispersal, disease and life-history evolution, Mathematical Biosciences, 2001, 173(1): 35–53.

    Article  MATH  MathSciNet  Google Scholar 

  5. Y. F. Li and J. G. Cui, The effect of constant and pulse vaccination on SIS epidemic models incorporating media coverage, Communications in Nonlinear Science and Numerical Simulation, 2009, 14(5): 2353–2365.

    Article  MATH  MathSciNet  Google Scholar 

  6. Z. Mukandavire, W. Garira, and J. M. Tchuenche, Modelling effects of public health educational campaigns on HIV/AIDS transmission dynamics, Applied Mathematical Modelling, 2009, 33(4): 2084–2095.

    Article  MATH  MathSciNet  Google Scholar 

  7. A. D’Innocenzo, F. Paladini, and L. Renna, A numerical investigation of discrete oscillating epidemic models, Physica A, 2006, 364(1): 497–512.

    Article  Google Scholar 

  8. S. J. Gao, L. S. Chen, and L. H. Sun, Dynamic complexities in a seasonal prevention epidemic model with birth pulses, Chaos, Solitons and Fractals, 2005, 26(4): 1171–1181.

    Article  MATH  MathSciNet  Google Scholar 

  9. A. Ramani, A. S. Carstea, R. Willox, and B. Grammaticos, Oscillating epidemics: A discrete-time model, Physica A, 2004, 333(1): 278–292.

    Article  MathSciNet  Google Scholar 

  10. V. Mendez and J. Fort, Dynamical evolution of discrete epidemic models, Physica A, 2000, 284(1–4): 309–317.

    Article  MathSciNet  Google Scholar 

  11. G. Z. Zeng, L. S. Chen, and H. Sun, Complexity of an SIR epidemic dynamics model with impulsive vaccination control, Chaos, Solitons and Fractals, 2005, 26(2): 495–505.

    Article  MATH  MathSciNet  Google Scholar 

  12. Y. N. Xiao, On an SIS epidemic model with stage structure, Journal of Systems Science & Complexity, 2003, 16(2): 275–288.

    MATH  Google Scholar 

  13. G. Seo and M. Kot, A comparison of two predator prey models with Holling’s type I functional response, Mathematical Biosciences, 2008, 212(3): 161–179.

    Article  MATH  MathSciNet  Google Scholar 

  14. G. W. Luo, Y. L. Zhang, and J. H. Xie, Bifurcation sequences of vibroimpact systems near a 1:2 strong resonance point, Nonlinear Analysis: Real World Applications, 2009, 10(1): 1–15.

    Article  MATH  MathSciNet  Google Scholar 

  15. E. Kaslik and St. Balint, Bifurcation analysis for a two-dimensional delayed discrete-time Hopfield neural network, Chaos, Solitons and Fractals, 2007, 34(4): 1245–1253.

    Article  MATH  MathSciNet  Google Scholar 

  16. A. Algaba, E. Gamero, and A. J. Rodrguez, A bifurcation analysis of a simple electronic circuit, Communications in Nonlinear Science and Numerical Simulation, 2005, 10(2): 169–178.

    Article  MATH  MathSciNet  Google Scholar 

  17. M. S. Peng, Z. H. Jiang, X. X. Jiang, et al., Multistability and complex dynamics in a simple discrete economic model, Chaos Solitons and Fractals, 2009, 41(2): 671–687.

    Article  MATH  MathSciNet  Google Scholar 

  18. S. G. Ruan and W. D. Wang, Dynamical behavior of an epidemic model with a nonlinear incidence rate, Journal of Differential Equations, 2003, 188(1): 135–163.

    Article  MATH  MathSciNet  Google Scholar 

  19. H. Broer, R. Roussarie, and C. Simo, Invariant circles in the Bogdanov-Takens bifurcation for diffeomorphisms, Ergodic Theory and Dynamical Systems, 1996, 16: 1147–1172.

    Article  MATH  MathSciNet  Google Scholar 

  20. Y. Kuznetsov, Elements of Applied Bifurcation Theory, Springer-Verlag, New York, 1998.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Systems Science, Northeastern University, Shenyang, 110004, China

    Na Yi & Qingling Zhang

  2. School of Sciences, Liaoning Shihua University, Fushun, 113001, China

    Na Yi

  3. School of Management, Shenyang University of Technology, Shenyang, 110870, China

    Peng Liu

  4. Department of Mathematics, The Hong Kong Polytechnic University, Hong Kong, China

    Yanping LIN

Authors
  1. Na Yi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qingling Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Peng Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yanping LIN
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qingling Zhang.

Additional information

This research is supported by the National Natural Science Foundation of China under Grant Nos. 60974004 and 71001074, and the Science Research Foundation of Department of Education of Liaoning Province of China under Grant No. W2010302.

This paper was recommended for publication by Editor Jinhu LÜ.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yi, N., Zhang, Q., Liu, P. et al. Codimension-two bifurcations analysis and tracking control on a discrete epidemic model. J Syst Sci Complex 24, 1033–1056 (2011). https://doi.org/10.1007/s11424-011-9041-0

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11424-011-9041-0

Key words

Search

Navigation