Skip to main content
SpringerLink
Log in

Orthogonalized lattice enumeration for solving SVP

  • Research Paper
  • Published:
Science China Information Sciences Aims and scope Submit manuscript

Abstract

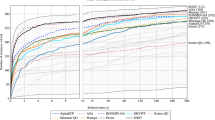
The orthogonalized integer representation was independently proposed by Ding et al. using genetic algorithm and Fukase et al. using sampling technique to solve shortest vector problem (SVP). Their results are promising. In this paper, we consider sparse orthogonalized integer representations for shortest vectors and propose a new enumeration method, called orthognalized enumeration, by integrating such a representation. Furthermore, we present a mixed BKZ method, called MBKZ, by alternately applying orthognalized enumeration and other existing enumeration methods. Compared to the existing ones, our methods have greater efficiency and achieve exponential speedups both in theory and in practice for solving SVP. Implementations of our algorithms have been tested to be effective in solving challenging lattice problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ajtai M, Kumar R, Sivakumar D. A sieve algorithm for the shortest lattice vector problem. In: Proceedings of the 33rd Annual ACM Symposium on Theory of Computing, Hersonissos, 2001. 601–610

    MATH  Google Scholar 

  2. Kannan R. Improved algorithms for integer programming and related lattice problems. In: Proceedings of the 15th Annual ACM Symposium on Theory of Computing. New York: ACM, 1983. 193–206

    Google Scholar 

  3. Nguyen P Q, Vidick T. Sieve algorithms for the shortest vector problem are practical. J Math Cryptol, 2008, 2: 181–207

    Article  MathSciNet  MATH  Google Scholar 

  4. Pujol X, Stehlé D. Solving the Shortest Lattice Vector Problem in Time 22.465n. IACR Cryptology ePrint Archive, Report 2009/605. http://perso.ens-lyon.fr/damien.stehle/downloads/2465.pdf

    Google Scholar 

  5. Wang X, Liu M, Tian C, et al. Improved Nguyen-Vidick heuristic sieve algorithm for shortest vector problem. In: Proceedings of the 6th ACM Symposium on Information, Computer and Communications Security, Hong Kong, 2011. 1–9

    Google Scholar 

  6. Micciancio D, Voulgaris P. A deterministic single exponential time algorithm for most lattice problems based on Voronoi cell computations. SIAM J Comput, 2013, 42: 1364–1391

    Article  MathSciNet  MATH  Google Scholar 

  7. Aggarwal D, Dadush D, Regev O, et al. Solving the shortest vector problem in 2n time using discrete Gaussian sampling. In: Proceedings of the 47th Annual ACM Symposium on Theory of Computing, Portland, 2015. 733–742

    MATH  Google Scholar 

  8. Lenstra A K, Lenstra H W, Lovász L. Factoring polynomials with rational coefficients. Math Ann, 1982, 261: 515–534

    Article  MathSciNet  MATH  Google Scholar 

  9. Schnorr C P, Euchner M. Lattice basis reduction: improved practical algorithms and solving subset sum problems. Math Program, 1994, 66: 181–199

    Article  MathSciNet  MATH  Google Scholar 

  10. Helfrich B. Algorithms to construct Minkowski reduced and Hermite reduced lattice bases. Theor Comput Sci, 1985, 41: 125–139

    Article  MathSciNet  MATH  Google Scholar 

  11. Hanrot G, Stehlé D. Improved analysis of Kannan’s shortest lattice vector algorithm. In: Proceedings of the 27th Annual International Cryptology Conference, Santa Barbara, 2007. 170–186

    MATH  Google Scholar 

  12. Fincke U, Pohst M. A procedure for determining algebraic integers of given norm. In: Proceedings of the European Computer Algebra Conference on Computer Algebra. Berlin: Springer, 1983. 194–202

    Google Scholar 

  13. Gama N, Nguyen P Q, Regev O. Lattice enumeration using extreme pruning. In: Proceedings of Annual International Conference on the Theory and Applications of Cryptographic Techniques, Monaco and Nice, 2010. 257–278

    MATH  Google Scholar 

  14. Shoup V. Number theory c++ library (ntl). http://www.shoup.net/ntl/

  15. Lindner R, Peikert C. Better key sizes (and attacks) for LWE-based encryption. In: Proceedings of Cryptographers’ Track at the RSA Conference, San Francisco, 2011. 319–339

    MATH  Google Scholar 

  16. Micciancio D, Regev O. Lattice-based cryptography. In: Post-Quantum Cryptography. Berlin: Springer, 2009. 147–191

    Chapter  Google Scholar 

  17. Rückert M, Schneider M. Estimating the Security of Lattice-based Cryptosystems. IACR Cryptology ePrint Archive, Report 2010/137. https://pdfs.semanticscholar.org/72de/2153c2f5fbe5769a739dfe7a4eb7cc9271de.pdf

    Google Scholar 

  18. Schnorr C P, Hörner H H. Attacking the Chor-Rivest cryptosystem by improved lattice reduction. In: Proceedings of the 14th Annual International Conference on Theory and Application of Cryptographic Techniques, Saint-Malo, 1995. 1–12

    MATH  Google Scholar 

  19. Haque M, Rahman M O, Pieprzyk J. Analysing progressive-BKZ lattice reduction algorithm. In: Proceedings of the 1st National Conference on Intelligent Computing and Information Technology, Chittagong, 2013. 73–80

    Google Scholar 

  20. Kuo P C, Schneider M, Dagdelen Ö, et al. Extreme enumeration on GPU and in clouds. In: Proceedings of the 13th International Workshop on Cryptographic Hardware and Embedded Systems, Nara, 2011. 176–191

    Google Scholar 

  21. Chen Y M, Nguyen P Q. BKZ 2.0: better lattice security estimates. In: Proceedings of International Conference on the Theory and Application of Cryptology and Information Security, Seoul, 2011. 1–20

    MATH  Google Scholar 

  22. Aono Y, Wang Y T, Hayashi T, et al. Improved progressive BKZ algorithms and their precise cost estimation by sharp simulator. In: Proceedings of Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, 2016. 789–819

    MATH  Google Scholar 

  23. Micciancio D, Walter M. Practical, predictable lattice basis reduction. In: Proceedings of Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, 2016. 820–849

    MATH  Google Scholar 

  24. Schnorr C P. Lattice reduction by random sampling and birthday methods. In: Proceedings of the 20th Annual Symposium on Theoretical Aspects of Computer Science. Berlin: Springer, 2003. 145–156

    Google Scholar 

  25. Ding D, Zhu G Z, Wang X Y. A genetic algorithm for searching the shortest lattice vector of SVP challenge. In: Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, 2015, 823–830

    Google Scholar 

  26. Fukase M, Kashiwabara K. An accelerated algorithm for solving SVP based on statistical analysis. J Inf Process, 2015, 23: 67–80

    Google Scholar 

  27. Holland J H. Adaptation in Natural and Artificial Systems. Ann Arbor: The University of Michigan Press, 1975

    Google Scholar 

  28. Booker L B, Goldberg D E, Holland J H. Classifier systems and genetic algorithms. Artif Intell, 1989, 40: 235–282

    Article  Google Scholar 

  29. Eiben A E, Aarts E H, Van Hee K M. Global convergence of genetic algorithms: a Markov chain analysis. In: Proceedings of International Conference on Parallel Problem Solving from Nature, Dortmund, 1990. 4–12

    Google Scholar 

  30. Goldberg D E, Holland J H. Genetic algorithms and machine learning. Mach Learn, 1988, 3: 95–99

    Article  Google Scholar 

  31. Schneider M, Gama N. SVP CHALLENGE. http://www.latticechallenge.org/svp-challenge/

  32. Aono Y, Wang Y, Hayashi T, et al. Progressive BKZ library. http://www2.nict.go.jp/security/pbkzcode/index.html

Download references

Acknowledgements

This work was supported by National Basic Research Program of China (973 Program) (Grant No. 2013CB834205), and National Natural Science Foundation of China (Grant No. 61133013). The authors would like to thank the anonymous reviewers for thorough and useful comments which have helped to improve the presentation of the paper.

Author information

Authors and Affiliations

  1. Department of Computer Science and Technology, Tsinghua University, Beijing, 100084, China

    Zhongxiang Zheng & Yang Yu

  2. Institute for Advanced Study, Tsinghua University, Beijing, 100084, China

    Xiaoyun Wang

  3. Key Laboratory of Cryptologic Technology and Information Security, Ministry of Education, Shandong Universtiy, Jinan, 250100, China

    Xiaoyun Wang

  4. Department of Electrical Engineering and Computer Sciences, University of Wisconsin, Milwaukee, WI, 53201, USA

    Guangwu Xu

Authors
  1. Zhongxiang Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaoyun Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guangwu Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yang Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaoyun Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zheng, Z., Wang, X., Xu, G. et al. Orthogonalized lattice enumeration for solving SVP. Sci. China Inf. Sci. 61, 032115 (2018). https://doi.org/10.1007/s11432-017-9307-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11432-017-9307-0

Keywords

Search

Navigation