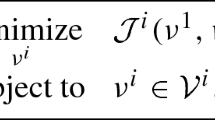Abstract
This paper yields sufficient conditions for existence of open loop Nash equilibria in certain types of nonlinear differential games satisfying certain monotonicity and/or convexity conditions.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
\(\tilde{U} _{i}\) has the weak\(^{*}\) topology. The weak\(^{*}\) topology on the unit ball in the dual of \(C(U)\) related to the scalar product \( \int _{U}\gamma (u)w(du), \gamma (.)\) continuous, can be metrizised, so this measurability is actually a metric measurability.
It is a consequence of the assumptions in the Theorem that \(\tilde{W}^{i}(\hat{w})\) (by standard existence theorems) and \(W_{*}\) are nonempty.
Without owns control dependence, to obtain this conclusion, we would have to assume instead of (9) that, in an obvious notation, \( N^{i}(t,x,w)=\{(\int f^{(i)}(t,x,u^{i},u^{-i})w(du^{-i})+\gamma _{i},\int g(t,x,u^{i},u^{-i})w(du^{-i}):u^{i}\in U_{i},\;\gamma _{i}\le 0\}\) is convex for all \(w=w^{-i}, t,x.\)
Using Remark 2, note that \(p_{0}^{i}\ne 0\) need only hold for \(u\in \tilde{W}(\hat{u}),\hat{u}\in W_{*},\) as \(W^{i}(\hat{w})\) is convex (see the proof below).
This assumption can be weakened, see next footnote.
Because \(W^{i}(\hat{u})\) is convex, by Remark 2, we can operate with a weaker assumption, namely that \(x_{0,\hat{u}^{2}}(T)\ge x_{T}\Rightarrow \) \(x_{0,\hat{u}^{2}}^{1}(T)>x_{T}^{1}\) and \(x_{\hat{u}^{1},0}(T)\ge x_{T}\Rightarrow x_{\hat{u}^{1},0}^{2}(T)>x_{T}^{2}\). If \(\ g^{i}\ge 0\) for \(\ x^{1},x^{2}\ge 0,\) \(g^{1}(0,x^{2}),g^{2}(x^{1},0)\le 0\) for all \( x^{1},x^{2},\) and \(x_{T}^{i}<x_{0}^{i},\) then \(x_{0,\hat{u}^{2}}(T)\ge x_{T}\) automatically implies \(x_{0,\hat{u}^{2}}^{1}(T)>x_{T\ }^{1}\).
Note that if \(0\in \tilde{W}^{1}(\hat{u}),\hat{u}\in W_{*},\) then \( x_{0,\hat{u}^{2}}^{1}(T)\ge x_{T}^{1}\) and \(x_{0,\hat{u}^{2}}^{2}(T)\ge x_{ \hat{u}^{1},\hat{u}^{2}}^{2}(T)\ge x_{T}^{2}.\)
[\(e(d)\)] equals [sup \(_{f\in B_{||.||^{*}}(\bar{f}(.,.),d)}\vert D\dot{x}_{f}(.)-D\dot{x}_{\bar{f}}(.)|],\) which in [10] is small by the continuity of \(x \rightarrow \bar{f}_{x}.\) When this continuity is uniform in \(x,\) uniformly in \(c\) (for \(\bar{f}=f(.,.,\tilde{u} (.),c))\), then [\(e(d)\)] is small uniformly in \(c.\) For more details, see Lemma 5.
References
Aubin, J.P., Ekeland, I.: Applied Nonlinear Analysis. Wiley, New York (1984)
Azevedo-Perdicoúlis T-P., Jank G.: Existence and uniqueness for disturbed open-loop Nash equilibria for affine-quadratic differential games. In: Advances in dynamic games, pp 25–39. Ann. Internat. Soc. Dynam. Games 11, Birkhäuser/Springer, New York (2011)
Buckdahn, R., Cardaliaguet, P., Rainer, C.: Nash equilibrium payoffs for nonzero-sum stochastic differential games. SIAM J. Control Optim. 43, 624–642 (2004)
Cardaliaguet, P., Plaskacz, S.: Existence and uniqueness of a Nash equilibrium feedback for a simple nonzero-sum differential game. Int. J. Game Theory 32, 33–71 (2003)
Davis, M.H.A.: Markov Models and Optimization. Chapman and Hall, London (1993)
Dieudonné, J.: Foundations of Modern Analysis. Academic Press, New York (1960)
Friedman, J.W.: Game Theory with Applications to Economics. Oxford University Press, New York (1986)
Nikol’skii, M.S.: On the existence of Nash equilibrium points for linear differential games in programmed strategies (Russian), Problems in dynamic control No1 222–229, Mosk. Gos Univ. im. Lomonosova, Fak. Vychisl. Mat. Kibern, Moscow (2005)
Scalzo, R.C., Williams, S.A.: On the existence of a Nash equilibrium point of N-person differential games. Appl. Math. Optim. 2(3), 271–278 (1976)
Seierstad, A.: A local attainability property for control systems defined by nonlinear ordinary differential equations in a Banach space. J. Differ. Equ. 8, 475–487 (1970)
Seierstad, A.: An extension to Banach space of Pontryagin’s maximum principle. J. Optim. Theory Appl. 17, 293–335 (1975)
Tolwinski, A., Haurie, A., Leitmann, G.: Cooperative equilibria in differential games. J. Math. Anal. Appl. 119, 182–202 (1986)
Author information
Authors and Affiliations
Corresponding author
Additional information
I am very grateful for comments received from two referees. It made it possible to improve the exposition and remove errors.
Rights and permissions
About this article
Cite this article
Seierstad, A. Existence of open loop Nash equilibria in certain types of nonlinear differential games. Optim Lett 8, 247–258 (2014). https://doi.org/10.1007/s11590-012-0565-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11590-012-0565-6