Skip to main content
SpringerLink
Log in

A least-squares approach for discretizable distance geometry problems with inexact distances

  • Original Paper
  • Published:
Optimization Letters Aims and scope Submit manuscript

Abstract

A branch-and-prune (BP) algorithm is presented for the discretizable distance geometry problem in \(\mathbb {R}^K\) with inexact distances. The algorithm consists in a sequential buildup procedure where possible positions for each new point to be localized are computed by using distances to at least K previously placed reference points and solving a system of quadratic equations. Such a system is solved in a least-squares sense, by finding the best positive semidefinite rank K approximation for an induced Gram matrix. When only K references are available, a second candidate position is obtained by reflecting the least-squares solution through the hyperplane defined by the reference points. This leads to a search tree which is explored by BP, where infeasible branches are pruned on the basis of Schoenberg’s theorem. In order to study the influence of the noise level, numerical results on some instances with distances perturbed by a small additive noise are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

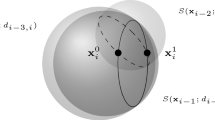
  1. As detailed in [19], the squared volume of the simplex defined by \(\{v_{i-K}, \dots , v_{i-1} \}\) is directly proportional to the absolute value of \(CM(\{v_{i-K}, \dots , v_{i-1} \})\).

  2. This sort of matrix is also known in the literature as nonnegative hollow matrix [1].

  3. In fact, if the problem is only to determine whether D is an EDM, without obtaining a realization, it is enough to obtain the smallest eigenvalue of G, e.g., by the inverse shifted power method.

  4. Recall the Frobenius norm of a matrix A is given by \(\Vert A \Vert _F^2 = \sum _{i} \sum _{j} a_{ij}^2 = \text {trace}(A^T A)\).

References

  1. Al-Homidan, S., Wolkowicz, H.: Approximate and exact completion problems for Euclidean distance matrices using semidefinite programming. Linear Algebra Appl. 406, 109–141 (2005)

    Article  MathSciNet  Google Scholar 

  2. Anderson, B.D.O., Shames, I., Mao, G., Fidan, B.: Formal theory of noisy sensor network localization SIAM. J. Discrete Math. 24, 684–698 (2010)

    MathSciNet  MATH  Google Scholar 

  3. Borg, I., Groenen, P.J.F.: Modern Multidimensional Scaling: Theory and Applications, 2nd edn. Springer Series in Statistics. Springer, New York (2005)

  4. Cassioli, A., Gunluk, O., Lavor, C., Liberti, L.: Discretization vertex orders in distance geometry. Discrete Appl. Math. 197, 27–41 (2015)

    Article  MathSciNet  Google Scholar 

  5. Drusvyatskiy, D., Krislock, N., Cheung Voronin, Y.-L., Wolkowicz, H.: Noisy Euclidean distance realization: robust facial reduction and the Pareto frontier. SIAM J. Optim. 27(4), 2301–2331 (2017)

    Article  MathSciNet  Google Scholar 

  6. Dokmanic, I., Parhizkar, R., Ranieri, J., Vetterli, M.: Euclidean distance matrices: essential theory, algorithms, and applications. IEEE Signal Process. Mag. 32(6), 12–30 (2015)

    Article  Google Scholar 

  7. Dong, Q., Wu, Z.: A linear-time algorithm for solving the molecular distance geometry problem with exact inter-atomic distances. J. Glob. Optim. 22, 365–375 (2002)

    Article  MathSciNet  Google Scholar 

  8. Dong, Q., Wu, Z.: A geometric build-up algorithm for solving the molecular distance geometry problem with sparse distance data. J. Glob. Optim. 26(3), 321–333 (2003)

    Article  MathSciNet  Google Scholar 

  9. Eckart, C., Young, G.: The approximation of one matrix by another of lower rank. Psychometrika 1, 211–218 (1936)

    Article  Google Scholar 

  10. Gonçalves, D.S., Mucherino, A.: Discretization orders and efficient computation of cartesian coordinates for distance geometry. Optim. Lett. 8, 2111–2125 (2014)

    Article  MathSciNet  Google Scholar 

  11. Gonçalves, D.S., Mucherino, A.: Optimal partial discretization orders for discretizable distance geometry. Int. Trans. Oper. Res. 23, 947–967 (2016)

    Article  MathSciNet  Google Scholar 

  12. Gonçalves, D.S., Mucherino, A., Lavor, C., Liberti, L.: Recent advances on the interval distance geometry problem. J. Glob. Optim. 69, 525–545 (2017)

    Article  MathSciNet  Google Scholar 

  13. Krislock, N., Wolkowicz, H.: Explicit sensor network localization using semidefinite representations and facial reductions. SIAM J. Optim. 20, 2679–2708 (2010)

    Article  MathSciNet  Google Scholar 

  14. Lavor, C., Lee, J., John, A.L.S., Liberti, L., Mucherino, A., Sviridenko, M.: Discretization orders for distance geometry problems. Optim. Lett. 6, 783–796 (2012)

    Article  MathSciNet  Google Scholar 

  15. Lavor, C., Liberti, L., Maculan, N., Mucherino, A.: The discretizable molecular distance geometry problem. Comput. Optim. Appl. 52, 115–146 (2012)

    Article  MathSciNet  Google Scholar 

  16. Lavor, C., Liberti, L., Mucherino, A.: The interval branch-and-prune algorithm for the discretizable molecular distance geometry problem with inexact distances. J. Glob. Optim. 56, 855–871 (2013)

    Article  MathSciNet  Google Scholar 

  17. Liberti, L., Lavor, C., Maculan, N.: A branch-and-prune algorithm for the molecular distance geometry problem. Int. Trans. Oper. Res. 15, 1–17 (2008)

    Article  MathSciNet  Google Scholar 

  18. Liberti, L., Masson, B., Lee, J., Lavor, C., Mucherino, A.: On the number of realizations of certain Henneberg graphs arising in protein conformation. Discrete Appl. Math. 165, 213–232 (2014)

    Article  MathSciNet  Google Scholar 

  19. Liberti, L., Lavor, C., Maculan, N., Mucherino, A.: Euclidean distance geometry and applications. SIAM Rev. 56, 3–69 (2014)

    Article  MathSciNet  Google Scholar 

  20. Luo, X., Wu, Z.: Least-squares approximations in geometric buildup for solving distance geometry problems. J. Optim. Theory Appl. 149, 580–598 (2011)

    Article  MathSciNet  Google Scholar 

  21. Mathar, R.: The best Euclidean fit to a given distance matrix in prescribed dimensions. Linear Algebra Appl. 67, 1–6 (1985)

    Article  MathSciNet  Google Scholar 

  22. Mucherino, A., Lavor, C., Liberti, L.: The discretizable distance geometry problem. Optim. Lett. 6, 1671–1686 (2012)

    Article  MathSciNet  Google Scholar 

  23. Mucherino, A., Liberti, L., Lavor, C.: MD-jeep: an implementation of a branch and prune algorithm for distance geometry problems, lectures notes in computer science 6327. In: Fukuda, K. et al. (eds.) Proceedings of the 3rd International Congress on Mathematical Software (ICMS10), Kobe, Japan, pp. 186–197 (2010)

  24. Saxe, J.B.: Embeddability of weighted graphs in \(k\)-space is strongly NP-hard. In: Proceedings of 17th Allerton Conference in Communications, Control and Computing, pp. 480–489. Monticello, IL (1979)

  25. Schoenberg, I.: Remarks to Maurice Fréchet’s article “Sur la définition axiomatique d’une classe d’espaces distanciés vectoriellement applicable sur l’espace de Hilbert”. Ann. Math. 36, 724–732 (1935)

    Article  MathSciNet  Google Scholar 

  26. Schönemann, P.H.: A generalized solution of the orthogonal procrustes problem. Psychometrika 31, 1–10 (1966)

    Article  MathSciNet  Google Scholar 

  27. Sit, A., Wu, Z., Yuan, Y.: A geometric buildup algorithm for the solution of the distance geometry problem using least-squares approximation. Bull. Math. Biol. 71, 1914–1933 (2009)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

I would like to thank Prof. Nathan Krislock for helping with SNLSDPClique package. I am grateful to the anonymous reviewers for their comments and suggestions that helped to improve this work. I also thank the Brazilian research agency CNPq for financial support.

Author information

Authors and Affiliations

  1. Universidade Federal de Santa Catarina, Florianópolis, Brazil

    Douglas S. Gonçalves

Authors
  1. Douglas S. Gonçalves
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Douglas S. Gonçalves.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gonçalves, D.S. A least-squares approach for discretizable distance geometry problems with inexact distances. Optim Lett 14, 423–437 (2020). https://doi.org/10.1007/s11590-017-1225-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11590-017-1225-7

Keywords

Search

Navigation