1 Introduction

Repetitive control (RC) or repetitive controller is a popular topic in control theory[1–10]. By the use of frequency-domain methods, the theories and applications in linear time-invariant (LTI) systems have developed very well[1–5]. On the other hand, compared with RC in LTI systems, RC in nonlinear systems has received limited research effort[6]. Currently, there exist two major approaches to design RCs for nonlinear systems[6]. One approach, namely the linearization approach, is to transform a nonlinear system into a linear system subject to a weak nonlinear term, then apply existing frequency-domain methods to the transformed linear system. The other major approach, namely the adaptive-control-like approach[7–10], is to convert a tracking problem for nonlinear systems into a rejection problem for nonlinear error dynamics, then apply existing adaptive-control-like design methods to the derived error dynamics. As mentioned above, the structures of RCs obtained for the linear and nonlinear systems are similar or the same, but the ways to obtain these RCs are different. For LTI systems, error dynamics are not required, whereas, for nonlinear systems, they are often required by using the adaptive-control-like approach. The requirement of error dynamics is also a key step in the general tracking design. However, this will not only restrict the development of RC but also fail to represent the special feature and importance of RC. For nonminimum phase nonlinear systems, it is difficult and computationally expensive to derive the error dynamics, especially when the internal dynamics are subject to an unknown disturbance. Because of this, we suppose that few RCs work on nonminimum phase nonlinear systems.

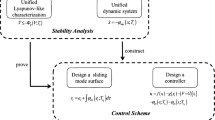
In this paper, we attempt to solve the rotational position tracking problem (RC problem) for a nonminimum phase nonlinear benchmark system called translational oscillator with a rotational actuator (TORA) and also known as rotational-translational actuator (RTAC)[11, 12]. It is pointed out that such RC problem is difficult to handle by both the linearization approach and the adaptive-control-like approach, because TORA is not globally feedback linearizable due to the weak, sinusoid-type nonlinear interaction between the translational oscillations and the rotational motion, and is also a nonminimum phase nonlinear system. For such purpose, we propose a new RC design under a recently developed additive-state-decomposition-based tracking control framework[13]. The key idea is to decompose the RC problem into two well-solved control problems by the additive state decompositionFootnote 1: an RC for an LTI system and a state feedback stabilizing control for a nonlinear system. Since the nonminimum phase RC problem is only confined to the LTI system, existing RC methods can be applied directly and the resulting closed-loop system can be analyzed in the frequency domain. On the other hand, the state feedback stabilization is considered for the decomposed nonlinear system. This implies that the nonminimum phase behavior is avoided. This is an important feature because nonminimum phase behavior will restrict the application of basic nonlinear controllers. Finally, one can combine the RC with the stabilizing controller to achieve the original control goal. The design processes of the linearization approach, the adaptive-control-like approach and the additive-state-decomposition-based approach are different, shown in Fig. 1.

Fig. 1
figure 1

Three RC design approaches

Full size image

This paper focuses on an RC problem, which is different from our previous work[14]. In the previous research, the external signals are generated by finite-dimensional exosystems, whereas the considered external signals here are generated by infinite-dimensional exosystems (any periodic signal can be generated by an infinite exosystems). To make the RC system robust, we propose for the considered nonlinear system a detailed filtered RC design. As a result, uniform ultimate boundness of tracking error instead of asymptotic stability is guaranteed. Therefore, most of the design procedures and proofs here are different from those in [14].

2 TORA benchmark problem

The translational oscillator with a rotating actuator system or rotational-translational actuator, has been widely used as a benchmark problem to test novel nonlinear control schemes[11]. After normalization and transformation, the TORA plant is simplified by the state-space representation as[12]

$$\matrix{{{{\dot x}_1} = {x_2}} \hfill \cr{{{\dot x}_2} = - {x_1} + \varepsilon \sin {x_3} + {d_2}} \hfill \cr{{{\dot x}_3} = {x_4}} \hfill \cr{{{\dot x}_4} = \tau} \hfill \cr{x(0) = {x_0}} \hfill \cr}$$
(1)

where 0 < ε < 1, τ ∈ R is the dimensionless control torque and d2 ∈ R is an unknown disturbance.

Two assumptions are made as follows:

  • Assumption 1. The disturbance d2 is a T-periodic signal, satisfying d2 (t) = d2 (t − T), t ≥ 0.

  • Assumption 2. All states \(x = {\left[ {{x_1}\quad {x_2}\quad {x_3}\quad {x_4}} \right]^{\rm{T}}} \in {{\bf{R}}^4}\) are measurable.

    Under Assumptions 1 and 2, the objective is to design controller τ such that the output y(t) = x3 (t) → r (t) as t → ∞, meanwhile keeping other states bounded, where \(r(t) \in (- {\pi \over 2},{\pi \over 2})\) is a T-periodic reference and its derivative is bounded.

  • Remark 1. The TORA is not globally feedback linearizable due to the weak, sinusoid-type nonlinear interaction ε sin x3 in (1). The internal dynamics of (1) are

    $$\matrix{{{{\dot x}_1} = {x_2}} \hfill \cr{{{\dot x}_2} = - {x_1}.} \hfill \cr}$$

    Since the internal dynamics are unstable (or say marginally stable), the considered problem is a tracking problem for a nonminimum phase nonlinear system.

  • Remark 2. In [15–19], the assumption on the disturbance is

    $$\left[ {\begin{array}{*{20}c} {\dot w_1 } \\ {\dot w_2 } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & \omega \\ { - \omega } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {w_1 } \\ {w_2 } \\ \end{array} } \right], d_2 = w_1 $$

    where ω > 0. In such case, d2 is a special periodic signal in the form of sin(ωt + φ), where φ ≥ 0. By contrast, the considered disturbance in Assumption 1, generated by an infinite-dimensional exosystem d2 (t)= d2 (t − T), is more general. The T-periodic disturbance may be generated from the vibration of other rotary mechanisms connected to the TORA plant.

3 Additive state decomposition of TORA benchmark

3.1 Additive state decomposition

In order to make the paper self-contained, the additive state decomposition[13] is recalled here briefly. Consider the following “original” system:

$$\matrix{{\dot x = f(t,x)} \hfill \cr{x(0) = {x_0}} \hfill \cr{y = h(t,x)} \hfill \cr}$$
(2)

where x ∈ Rn and y ∈ Rm. Two systems, denoted by the primary system and (derived) secondary system are defined as

$$\matrix{{{{\dot x}_p} = {f_p}(t,{x_p},{x_s})} \hfill \cr{{x_p}(0) = {x_p},0} \hfill \cr{{y_p} = {h_p}(t,{x_p})} \hfill \cr}$$
(3)

and

$$\matrix{{{{\dot x}_s} = f(t,{x_p} + {x_s}) - {f_p}(t,{x_p},{x_s})} \hfill \cr{{x_s}(0) = {x_0},{x_{p,0}}} \hfill \cr{{y_s} = h(t,{x_p} + {x_s}) - {h_p}(t,{x_p})} \hfill \cr}$$
(4)

where x s ≜ x − x p and y s ≜ y − y p . The secondary system (4) is determined by the original system (2) and the primary system (3). From the definition, we have

$$x(t) = {x_p}(t) + {x_s}(t),y(t) = {y_p}(t) + {y_s}(t),t \geq 0.$$
(5)

3.2 Additive state decomposition of TORA benchmark

The controller τ in (1) is designed as

$$\tau = {K^{\rm{T}}}x + u$$

where K ∈ R4 and u ∈ R will be specified later. Then, system (1) becomes

$$\matrix{{\dot x\left({{A_0} + B{K^{\rm{T}}}} \right)x + Bu + \phi (y) + d} \hfill \cr{y = {C^{\rm{T}}}x,\quad x(0) = {x_0}} \hfill \cr}$$
(6)

where

$$A_0 = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ { - 1} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right],B = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 1 \\ \end{array} } \right],C = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ 0 \\ \end{array} } \right],\varphi (y) = \left[ {\begin{array}{*{20}c} 0 \\ {\varepsilon \sin y} \\ 0 \\ 0 \\ \end{array} } \right],d = \left[ {\begin{array}{*{20}c} 0 \\ {d_2 } \\ 0 \\ 0 \\ \end{array} } \right].$$

By taking (6) as the “original” system, the primary system is chosen to be an LTI system including all external signals as

$$\matrix{{{{\dot x}_p} = A{x_p} + B{u_p} + {d_p}} \hfill \cr{{y_p} = {C^{\rm{T}}}{x_p}} \hfill \cr{{x_p}(0) = {x_0}} \hfill \cr}$$
(7)

where A = A0 + εD (C + aB)T + BKT, d p = ϕ (r) − εD (r + aṙ) + d and \(D = {\left[ {0\quad 1\quad 0\quad 0} \right]^{\rm{T}}}\). Then, according to (4), the secondary system is derived from the original system (6) and the primary system (7) as

$$\matrix{{{{\dot x}_s} = \left({{A_0} + B{K^{\rm{T}}}} \right){x_s} + (\phi ({y_p} + {y_s}) - \phi (r)) -} \hfill \cr{\quad \quad \varepsilon D\left({{{(C + aB)}^{\rm{T}}}{x_p} - (r + a\dot r)} \right) + B{u_s}} \hfill \cr{{y_s} = {C^{\rm{T}}}{x_s},\quad {x_s}(0) = 0} \hfill \cr}$$
(8)

where u s = u − u p . So, it follows

$$\matrix{{x = {x_p} + {x_s}} \hfill \cr{y = {y_p} + {y_s}} \hfill \cr{u = {u_p} + {u_s}.} \hfill \cr}$$
(9)

As shown in Fig. 2, the TORA benchmark (6) is decomposed into two systems by the additive state decomposition: an LTI “primary” system (7), leaving the secondary system (8) subject to the nonlinear term ϕ (·). The nonminimum phase RC task is only assigned to the LTI system (7). On the other hand, the task of handling nonlinearity is only assigned to the secondary system (8), where nonminimum phase behavior is avoided. More concretely, design an RC u p to drive y p → r in (7), and design u s to drive y s ultimately bounded with respect to y p − r, namely y s → 0 as y p − r. If so, then y = y p + y s → r by designing u = u p +u s . Obviously, the two tasks are easier than the original one. Therefore, the original tracking problem is simplified by the additive state decomposition.

  • Remark 3. For a class of nonminimum phase systems with measurable nonlinearities and unknown disturbances, readers can find a rule to use the additive state decomposition[13]. However, besides the rule, a term εD (C + aB)T x p − εD (r + aṙ) is introduced additionally into (7) and (8). Note that (C + aB)T x p = y p + aẏ p , so the additional term \(\varepsilon D = \left({{{(C + aB)}^{\rm{T}}}{x_p} - (r + a\dot r)} \right)\) in (8) will vanish as y p → r and ẏ p → ṙ. Thanks to the additional term, the pair \(\left({{A_0} + \varepsilon D{{(C + aB)}^{\rm{T}}},B} \right)\) is controllable, whereas the pair (A0, B) is uncontrollable. Therefore, there always exists a gain K such that the matrix A is a stable matrix.

  • Remark 4. The primary system (7) does not contain the state x s , namely it is independent of the secondary system (8). On the other hand, the secondary system (8) depends on the output of primary system (7). If y p has tracked r, namely y p = r, then the primary system (7) and the secondary system (8) are decoupled. According to these, the two controllers can be designed separately.

Fig. 2
figure 2

Additive state decomposition of TORA

Full size image

4 An additive-state-decomposition approach

So far, we have decomposed the transformed system into two subsystems in charge of corresponding subtasks. In this section, we are going to investigate controller design with respect to the two component subtasks respectively.

4.1 Filtered repetitive controller design for primary system

Define a filtered tracking error as

$${e_p} = {\tilde y_p} + a{\dot \tilde y_p}$$
(10)

where \({\tilde y_p} = {y_p} - r\) and a > 0. It is easy to see that both \({\tilde y_p}\) and \({\dot \tilde y_p}\) can be viewed as outputs of a stable system with e p as input, which means that \({\tilde y_p}\) and \({\dot \tilde y_p}\) are bounded if e p is bounded. In addition, \({\tilde y_p}(t) \to 0\) and \({\dot \tilde y_p}(t) \to 0\) as long as e p (t) → 0. Inspired by the design in [8], the filtered RC u p is designed as

$$\matrix{{\epsilon\dot \xi (t) = - \xi (t) + (1 - {\epsilon^2})\xi (t - T) + {L_1}{e_p}(t)} \hfill \cr{{u_p}(\xi ,{x_p},r) = L_2^{\rm{T}}{x_p}(t) + {L_3}\xi (t)} \hfill \cr{\xi (s) = 0,s \in [ - T,0]} \hfill \cr}$$
(11)

where L1, L3 ∈ R and L2 ∈ R4 will be specified later. With the relation (11), one has

$${e_p}(s) = {1 \over {{L_1}}}p(s)\xi (s)$$

where p (s)= ∊s + 1 − (1 − ∊2) e−sT. Then, the closed-loop system corresponding to the primary system (7) and (11) gives

(12)

The transfer function from d a to e p is

$$e_p (s) = \frac{1} {{L_1 }}p(s)\xi (s) = \underbrace {\frac{1} {{L_1 }}C_a^T \left( {sE - A_a - A_{a - T^{e^{ - sT} } } } \right) - ^1 p(s)}_{G(s)}d_a (s)$$
(13)

where \({C_a} = {\left[ {1\quad 0\quad 0\quad 0\quad 0} \right]^{\rm{T}}}\) The relation (13) can be rewritten as

$${e_p}(s) = \underbrace {{1 \over {{L_1}}}C_a^{\rm{T}}{{\left({sE - {A_a} - {A_{a, - T}}{{\rm{e}}^{- sT}}} \right)}^{- 1}}}_{{\rm{New}}\;{\rm{transfer}}\;{\rm{function}}}\underbrace {p(s){d_a}(s)}_{{\rm{New}}\;{\rm{input}}}.$$

Since d a is a T-periodic signal, ℒ−1 (p(s) d a (s)) will be with a small ultimate bound, where ℒ−1 (·) denotes the inverse Laplace transform. Especially, p (s) = 1 − e−sT and ℒ−1 (p(s) d a (s)) → 0if ∊ =0 According to this, only the stability of G (s) (or (12) without the external signal d a ) needs to be considered. An easy parameter choice rule is given in Theorem 1 to ensure the stable G (s).

  • Theorem 1. Suppose that the parameters in (11) are chosen as

    $$\matrix{{{L_1} = {\kappa _1}} \hfill \cr{{L_2} = H - K} \hfill \cr{{L_3} = - {2 \over a}{\kappa _1}} \hfill \cr}$$
    (14)

    where \(0 < \varepsilon < 1,{\kappa _1} > 0,{\kappa _2} > 2\) and \(H = - {1 \over a}{\left[ {0\quad \varepsilon \quad \kappa \quad 1 + {\kappa _2}} \right]^{\rm{T}}}\) Then, 1) without external signal d a , (12) is exponentially stable for any 0 < ∊ < 1; 2) in (12), ∥x p ∥ and ∥ξ∥ are bounded on [0, ∞) and there exists δ > 0 such thatFootnote 2 \({\left\| {{{\tilde y}_p}} \right\|_a} \le \delta\) and \({\left\| {{{\dot \tilde y}_p}} \right\|_a} \le \delta\).

  • Proof. See Appendix A. □

  • Remark 5. Since the closed-loop system (12) is an LTI system, various frequency domain methods are applicable, such as the bode plot, to analyze the tracking (rejection) accuracy. This will be shown in the following numerical simulation. It should be pointed out that other RCs can be also designed for the primary system (7).

4.2 Stabilizing controller design for secondary system

Since \({\left\| {{{\tilde y}_p}} \right\|_a} \le \delta\) and \({\left\| {{{\dot \tilde y}_p}} \right\|_a} \le \delta\), it is expected that the ultimate bound of ∥x s ∥ can be adjusted by δ. For example, there exists γ > 0, such that ∥x s ∥ a ≤ γδ. If so, we have ∥y − r∥ a ≤ (1 + γ) δ.

The secondary system (8) can be rewritten as

$$\matrix{{{{\dot x}_{1,s}} = {x_{2,s}}} \hfill \cr{{{\dot x}_{2,s}} = - {x_{1,s}} + \varepsilon \sin ({x_{3,s}} + r) - \varepsilon \sin r + g} \hfill \cr{{{\dot x}_{3,s}} = {x_{4,s}}} \hfill \cr{{{\dot x}_{4,s}} = {K^{\rm{T}}}{x_s} + {u_s}} \hfill \cr{{x_s}(0) = 0} \hfill \cr}$$
(15)

where g = ϕ(y p + x3, s) − ϕ(r + x3, s) − εD (C + aB)T x p + εD (r + aṙ). The following constructive procedure is also given in [14]. However, in order to make the paper self-contained, the design is recalled here briefly. Since \({\left\| {{{\tilde y}_p}} \right\|_a} \le \delta\), the proof is different from that in [14]. The controller design procedure starts from the marginally stable (x1, s, x2, s)-subsystem.

  • Step 1. Consider the (x1, s, x2, s)-subsystem of (16) with x3, s viewed as the virtual control input. The derivative of the quadratic function \({V_1} = x_{1,s}^2 + x_{2,s}^2\) is

    $${\dot V_1} = 2\varepsilon {x_{2,s}}[\sin ({x_{3,s}} + r) - \sin r] + 2{x_{2,s}}g.$$
    (16)

    Then, the following “certainty equivalence” (CE) based virtual controller is introduced as

    $${x_{3,s}} = - b\arctan {x_{2,s}} + x_{3,s}^{\prime}$$
    (17)

    where b ∊ R. Since

    $$\matrix{{\varepsilon \sin ({x_{3,s}} + r) - \varepsilon \sin r =} \hfill \cr{\quad \quad \varepsilon \sin (- b\arctan {x_{2,s}} + x_{3,s}^{\prime} + r) - \varepsilon \sin r =} \hfill \cr{\quad \quad \varepsilon \sin (- b\arctan {x_{2,s}} + r) - \varepsilon \sin r +} \hfill \cr{\quad \quad \varepsilon \sin (- b\arctan {x_{2,s}} + x_{3,s}^{\prime} + r) -} \hfill \cr{\sin (- b\arctan {x_{2,s}} + r)] =} \hfill \cr{2\varepsilon \sin \left({{{- b\arctan {x_{2,s}}} \over 2}} \right)\cos \left({{{- b\arctan {x_{2,s}} + 2r} \over 2}} \right)} \hfill \cr{\varepsilon [\sin (- b\arctan {x_{2,s}} + x_{3,s}^{\prime} + r) -} \hfill \cr{\;\sin (- b\arctan {x_{2,s}} + r)} \hfill \cr}$$

    the (x1, s, x2, s)-subsystem of (16) becomes

    $$\matrix{{{{\dot x}_{1,s}} = {x_{2,s}}} \hfill \cr{{{\dot x}_{2,s}} = - {x_{1,s}} + {g^{\prime}} +} \hfill \cr{\quad \;2\varepsilon \sin \left({{{- b\arctan {x_{2,s}}} \over 2}} \right)\cos \left({{{- b\arctan {x_{2,s}} + 2r} \over 2}} \right)} \hfill \cr}$$
    (18)

    where

    $$\matrix{{{g^{\prime}} = \varepsilon \sin (- b\arctan {x_{2,s}} + r + x_{3,s}^{\prime}) -} \hfill \cr{\quad \varepsilon \sin (- b\arctan {x_{2,s}} + r) + g.} \hfill \cr}$$
    (19)

    In order to ensure \(\cos \left({{{- b\arctan {x_{2,s}} + 2r} \over 2}} \right) > 0\), the parameter b has to satisfy \(0 < b < {\min _t}2\left({1 - {{2|r(t)|} \over \pi}} \right)\). Since \(r(t) \in (- {\pi \over 2}, - {\pi \over 2}),b\), b always exists. If \(x_{3,s}^\prime \equiv 0\) and g = 0, then \(g \equiv 0\) g ≡0, then \({\dot V_1} \le 0\) (see Appendix B).

  • Step 2. The backstepping design is applied to the \((x_{3,s}^\prime ,{x_{4,s}})\)-subsystem such that a nonlinear controller u s drives \(x_{3,s}^\prime\) to the origin. With the aid of (16) and (18), the time derivative of the new variable \(x_{3,s}^\prime\) is

    $$\dot x_{3,s}^{\prime} = {x_{4,s}} + \psi + b{1 \over {1 + x_{2,s}^2}}g$$
    (20)

    where \(\psi = b{1 \over {1 + x_{2,s}^2}}[ - {x_{1,s}} + \varepsilon \sin ({x_{3,s}} + r) - \varepsilon \sin r]\). A new variable \(x_{4,s}^\prime\) is defined as

    $$x_{4,s}^{\prime} = x_{3,s}^{\prime} + {x_{4,s}} + \psi .$$
    (21)

    Then, (21) becomes

    $$\dot x_{3,s}^{\prime} = - x_{3,s}^{\prime} + x_{4,s}^{\prime} + b{1 \over {1 + x_{2,s}^2}}g.$$

    By the definition (22), the time derivative of the new variable \(x_{3,s}^\prime\) is

    $$\matrix{{\dot x_{4,s}^{\prime} = \dot x_{3,s}^{\prime} + {{\dot x}_{4,s}} + \dot \psi =} \hfill \cr{\quad \;\; - x_{3,s}^{\prime} + x_{4,s}^{\prime} + b{1 \over {1 + x_{2,s}^2}}g + {K^{\rm{T}}}{x_s} + {u_s} + \dot \psi .} \hfill \cr}$$

    Therefore, u s for the secondary system (16) is designed as

    $${u_s}({x_p},{x_s},r) = x_{3,s}^{\prime} - 2x_{4,s}^{\prime} - {K^{\rm{T}}}{x_s} - \dot \psi .$$
    (22)

    Then, the \((x_{3,s}^\prime ,x_{4,s}^\prime)\)-subsystem becomes

    $$\matrix{{\dot x_{3,s}^{\prime} = - x_{3,s}^{\prime} + x_{4,s}^{\prime} + b{1 \over {1 + x_{2,s}^2}}g} \hfill \cr{\dot x_{4,s}^{\prime} = - x_{4,s}^{\prime} + b{1 \over {1 + x_{2,s}^2}}g.} \hfill \cr}$$
    (23)

    We are now ready to state the theorem for the secondary system (8).

  • Theorem 2. Suppose \({\left\| {{{\tilde y}_p}} \right\|_a} \le \delta\) and \({\left\| {{{\dot \tilde y}_p}} \right\|_a} \le \delta\), where δ is sufficiently small. The controller u s for the secondary system (16) is designed as (23), where \(0 < b < {\min _t}2\left({{{1 - 2|r(t)|} \over \pi}} \right)\). Then, there exists γ > 0 such that ∥x s ∥ a ≤ γδ and ∥x s ∥ is bounded on [0, ∞).

  • Proof. See Appendix B. □

  • Remark 6. As shown above, the controller design for the secondary system is somewhat complex. However, without the additive state decomposition, the controller design for the original tracking problem will be more complex. The additive state decomposition in fact makes the design more clear.

4.3 Controller synthesis for original system

It should be noticed that the controller design above is based on the condition that x p and x s are known a prior. A problem arises that the states x p and x s cannot be measured directly except for x = x p + x s . Taking this into account, the following observer is proposed to estimate the states x p and x s . Unlike the traditional concept of observers, the proposed observer can estimate the states of the primary system and the secondary system directly, not asymptotically or exponentially. This can be explained that, unlike a real system, either the primary system or the secondary system is in fact virtual whose initial values can be assigned freely by designers.

An observer based on the secondary system (8) can estimate x s , which is stated in Theorem 3.

  • Theorem 3. Suppose matrix A to be stable. Then, the observer

    $$\matrix{{{{\dot \hat x}_s} = A{{\hat x}_s} + \phi (y) - \phi (r) -} \hfill \cr{\varepsilon D{{(C + aB)}^{\rm{T}}}x + \varepsilon D(r + a\dot r) + B{u_s}} \hfill \cr{{{\hat x}_p} = x - {{\hat x}_s}} \hfill \cr{{{\hat x}_s}(0) = 0} \hfill \cr}$$
    (24)

    satisfies

    $${\hat x_p} \equiv {x_p}\;{\rm{and}}\;{\hat x_s} \equiv {x_s}.$$

  • Proof. With the aid of the relation x p = x − x s , the secondary system (8) can also be written as

    $$\matrix{{{{\dot x}_s} = A{x_s} + \phi (y) - \phi (r) -} \hfill \cr{\quad \varepsilon D{{(C + aB)}^{\rm{T}}}x + \varepsilon D(r + a\dot r) + B{u_s}} \hfill \cr}$$
    (25)

    where x s 0) = 0. Subtracting (26) from (25) results in

    $$\matrix{{{{\dot \tilde x}_s} = A{{\tilde x}_s}} \hfill \cr{{{\tilde x}_s}(0) = 0} \hfill \cr}$$
    (26)

    where \({\tilde x_s} = {\hat x_s} - {x_s}\). Then, \({\hat x_p} \equiv {x_p}\) and \({\hat x_s} \equiv {x_s}\). □

  • Remark 7. The measurement x and parameters may be inaccurate. In this case, it is expected that small uncertainties lead \({\hat x_p}\) close to x p (or \({\hat x_s}\) close to x s ). From (27), a stable matrix A can guarantee a small \({\tilde x_s}\) in the presence of small uncertainties.

  • Theorem 4. Suppose that the conditions of Theorems 1–3 hold. If the controller τ in system (1) is designed as

    $$\matrix{{\epsilon \dot \xi (t) = - \xi (t) + (1 - {\epsilon ^2})\xi (t - T) +} \hfill \cr{\quad \quad {L_1}\left({{{(C + aB)}^{\rm{T}}}{{\hat x}_p} - r - a\dot r} \right)(t)} \hfill \cr{\;\;\tau (t) = {K^{\rm{T}}}x(t) + {u_p}(\xi ,{{\hat x}_p},r) + {u_s}({{\hat x}_p},{{\hat x}_s},r)} \hfill \cr}$$
    (27)

    where ξ (s) = 0, s ∈ [−T, 0], \({\hat x_p}\) and \({\hat x_s}\) are given by (25), u p (·) is defined as in (11), and u s (·) is defined as in (23). Then, 1) ∥x∥ and ∥ξ∥ are bounded on [0, ∞) and 2) there exists ρ > 0 such that ∥y − r∥ a ≤ ρδ, where \({\left\| {{{\tilde y}_p}} \right\|_a} \le \delta\) and \({\left\| {{{\dot \tilde y}_p}} \right\|_a} \le \delta\).

  • Proof. Note that the original system (1), the primary system (7) and the secondary system (8) have the relation: x = x p + x s and y = y p + y s . With the controller, for the primary system (7), ∥x p ∥, ∥ξ∥ are bounded on [0, ∞), \({\left\| {{{\tilde y}_p}} \right\|_a} \le \delta ,{\left\| {{{\dot \tilde y}_p}} \right\|_a} \le \delta\) by Theorem 1. On the other hand, for the secondary system (8), there exists γ > 0 such that ∥x s ∥ a ≤ γδ and ∥x s ∥ is bounded on [0, ∞) by Theorem 2. Theorem 3 ensures that \({\hat x_p} \equiv {x_p}\) and \({\hat x_s} \equiv {x_s}\). Therefore, 1) ∥x∥ and ∥ξ∥ are bounded on [0, ∞) and 2) there exists ρ > 0 such that ∥y − r∥ a ≤ ρδ, where \({\left\| {{{\tilde y}_p}} \right\|_a} \le \delta\) and \({\left\| {{{\dot \tilde y}_p}} \right\|_a} \le \delta\). □

The closed-loop control system is shown in Fig. 3, which includes the TORA plant (1), the controller (28) and the observer (25).

Fig. 3
figure 3

Closed-loop control system of TORA

Full size image

5 Numerical simulation

In the simulation, we set ε =0.2 and the initial value \({x_0} = {\left[ {0.1\quad 0\quad 0\quad 0} \right]^{\rm{T}}}\) in (1). The reference r is chosen to be \(r(t) = 0.5\sin (\sin {{2\pi} \over T}t)\), and the disturbance \({d_2}(t) = 0.1\cos ({{2\pi} \over T}t)\), where the period T = 3. The objective here is to design controller τ such that the output y (t) − r (t) is uniformly ultimately bounded with a small ultimate bound. Meanwhile, other states are bounded.

The parameters are chosen as a = 1 and \(K = {\left[ {0\quad - \varepsilon \quad - 1\quad - 2} \right]^{\rm{T}}}\). Then, A in (7) satisfies

$$\max {\mathop{\rm Re}\nolimits} (\lambda (A)) = - 0.01 < 0.$$

Furthermore, according to Theorem 1, the parameters of the controller (28) are chosen as ε = 0.01, L1 =2, L2 = 04 × 1 and L3 = −4. The parameter b is chosen as \(\epsilon = 0.01,{L_1} = 2,{L_2} = {0_{4 \times 1}}\).

In (13), let G (s) = [g1(s) g2(s) g3(s) g4(s) g5(s)]. With the chosen parameters above, |g i (jω)|, i = 1, 2, ⋯, 5, with respect to frequency ω are plotted in Fig. 4. As shown, all |g i (jω)| have comb shape with notches matching the frequencies of the considered periodic signals. This makes |g i (jω)| close to zero at \(\omega = k{{2\pi} \over T},k = 0,1, \cdots\), k = 0, 1, ⋯, in the low frequency band. Since low frequencies dominate d a (t), it is expected that e p is with a small ultimate bound.

Fig. 4
figure 4

Amplitude response of the transfer function of elements of G (s) in (13). In this example, the last two elements |g4 (jω)| and |g5 (jω)| are the same. Therefore, it seems that there are only four curves in the figure.

Full size image

The TORA plant (1) is driven by the controller (28) with the parameters above. The evolutions of all states of (1) are shown in Fig. 5. From the simulation, it can be seen that the proposed controller τ drives the tracking error y (t) − r (t) to be uniformly ultimately bounded with a small ultimate bound. Meanwhile, other states are bounded. In Fig. 6, the evolutions of state and control inputs of the decomposed systems are shown. Moreover, the final control input is also plotted. As shown, the ultimate bound of ∥x s ∥ is small and the control u = u p + u s is bounded.

Fig. 5
figure 5

Evolutions of all states

Full size image
Fig. 6
figure 6

Evolutions of all states and inputs of the primary system (7) and the secondary system (8)

Full size image

6 Conclusions

In this paper, the rotational position tracking problem for TORA was solved by the proposed additive-state-decomposition-based RC. The design relied on additive state decomposition, by which the considered RC problem was decomposed into an RC problem for a “primary” LTI system and a “secondary” state-feedback stabilization problem for a nonlinear system. For the LTI system, an easy RC design is given. Thanks to its linearity, the amplitude response is applied to show the tracking accuracy Fig. 4. On the other hand, the backstepping design is applied to the state-feedback stabilization problem. This makes RC design for TORA tractable and flexible. Future works on TORA include designing RC for translational displacement tracking problem and improving the robustness of the resulting closed-loop RC system.