Parameter estimation for coherently distributed noncircular sources under impulsive noise environments

Abstract

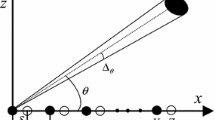
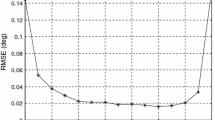
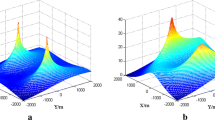
The signal source generates angular expansion in space due to scattering, reflection and other phenomena in a complex environment, which requires a distributed signal model for processing. This paper extends the method of joint angular estimation for coherently distributed (CD) sources consisting of noncircular signals to the impulsive noise scenario. In an actual wireless passive positioning environment, impulsive noise is very common. However, most algorithms only consider Gaussian noise environments and are not suitable for angle estimation in impulsive noise scenarios. This paper proposes the generalized complex correntropy (GCC) and shows that it can eliminate the effects of outliers in an impulsive noise environment. This is because the complex correntropy is an effective tool to analyze higher-order statistical moments in the impulsive noise environment. In order to improve the accuracy of the estimation, we construct a GCC matrix based on extended array output and apply the subspace techniques to extract the angle information of the CD noncircular sources. The simulation results show that the estimation performance of the proposed algorithms is better than the traditional algorithm applied to the noncircular CD sources.

Appendix: The Proof of the boundedness of GCC

Here, we can rewrite the GCC operator as:

$$ \begin{aligned} & V_{\text{GCC}} \left( {C_{1} ,C_{2} } \right) \\ & \quad = E\left[ {\frac{1}{{2\pi \Delta^{2} }}\exp \left( { - \frac{{\left( {C_{1} - C_{2} } \right)\left( {C_{1} - C_{2} } \right)^{*} }}{{2\Delta^{2} }}} \right)C_{1} C_{2}^{*} } \right] \end{aligned} $$

(B1)

Analysis of (B1) as follows

$$ \begin{aligned} & V_{GCC} \left( {C_{1} ,C_{2} } \right) \\ & \quad \le E\left[ {\left| {\frac{1}{{2\pi \Delta^{2} }}\exp \left( { - \frac{{\left( {C_{1} - C_{2} } \right)\left( {C_{1} - C_{2} } \right)^{*} }}{{2\Delta^{2} }}} \right)C_{1} C_{2}^{*} } \right|} \right] \\ & \quad \le E\left[ {\left| {C_{1} C_{2}^{*} } \right|} \right] \end{aligned} $$

(B2)

As mentioned above that let $C_{1}$ and $C_{2}$ be i.i.d. SαS complex random variables, under this assumption $C_{1}$ and $C_{2}^{*}$ must be also i.i.d. So we have

$$ V_{\text{GCC}} \left( {C_{1} ,C_{2} } \right) \le E\left[ {\left| {C_{1} C_{2}^{*} } \right|} \right] = E\left[ {\left| {C_{1} } \right|} \right]E\left[ {\left| {C_{2}^{*} } \right|} \right] $$

(B3)

From [10] we know that for the SαS random variable $X$ with the characteristic exponent $1 < \alpha \le 2$, there exists

$$ E\left[ {\left| X \right|^{p} } \right] = \frac{{2^{p + 1} \varGamma \left( {\frac{p + 1}{2}} \right)\varGamma \left( { - p/\alpha } \right)}}{{\alpha \sqrt \pi \varGamma \left( { - p/2} \right)}}\gamma^{{\frac{p}{\alpha }}} \quad {\text{for}}\;0 < p < \alpha $$

(B4)

$\varGamma \left( \cdot \right)$ is the gamma function defined by $\varGamma \left( x \right) = \int_{0}^{\infty } {t^{x - 1} e^{ - t} {\text{d}}t}$.

Obviously substituting $p$ with 1 in (B4) can get a finite value $E[|C_{1} |] \le + \infty$. So

$$ V_{\text{GCC}} \left( {C_{1} ,C_{2} } \right) \le + \infty $$

(B5)

which means that $V_{\text{GCC}}$ is bounded.