A Note on Modified Hermite Interpolation

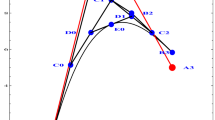
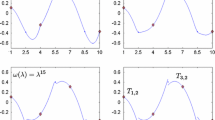
Abstract

We discuss the problem of fitting a smooth regular curve $\gamma {:}[0,T]{\rightarrow }\mathbb {E}^n$ based on reduced data$Q_m = \{q_i\}_{i = 0}^m$ in arbitrary Euclidean space $\mathbb {E}^n$. The respective interpolation knots ${\mathcal T} = \{t_i\}_{i = 0}^m$ satisfying $q_i = \gamma (t_i)$ are assumed to be unknown. In our setting the substitutes ${\mathcal T}_{\lambda }=\{{\hat{t}}_i\}_{i = 0}^m$ of ${{\mathcal {T}}}$ are selected according to the so-called exponential parameterization governed by $Q_m$ and $\lambda \in [0,1]$. A modified Hermite interpolant $\hat{\gamma }^H$ introduced in Kozera and Noakes (Fundam Inf 61(3–4):285–301, 2004) is used here to fit $(\hat{{\mathcal {T}}}_{\lambda },Q_m)$. The case of $\lambda = 1$ (i.e. for cumulative chords) for general class of admissible samplings yields a sharp quartic convergence order in estimating $\gamma {\in } C^4$ by ${\hat{\gamma }}^H$ [see Kozera (Stud Inf 25(4B–61):1–140, 2004) and Kozera and Noakes (Fundam Inf 61(3–4):285–301, 2004)]. As recently shown in Kozera and Wilkołazka (Math Comput Sci, 2018. https://doi.org/10.1007/s11786-018-0362-4) the remaining $\lambda \in [0,1)$ render a linear convergence order in ${\hat{\gamma }}^H\approx \gamma$ for any $Q_m$ sampled more-or-less uniformly. The related analysis relies on comparing the difference $\gamma -{\hat{\gamma }}^H\circ \phi ^H$ in which $\phi ^H$ forms a special mapping between [0, T] and $[0,{\hat{T}}]$ with ${\hat{T}} = {\hat{t}}_m$. In this paper: (a) several sufficient conditions enforcing $\phi ^H$ to yield a genuine reparameterization are first formulated and then analytically and symbolically simplified. The latter covers also the asymptotic case expressed in a simple form. Ultimately, the reformulated conditions can be algebraically verified and/or geometrically visualized, (b) additionally in Sect. 3, the sharpness of the asymptotics of $\gamma -{\hat{\gamma }}^H\circ \phi ^H$ [from Kozera and Wilkołazka (Math Comput Sci, 2018. https://doi.org/10.1007/s11786-018-0362-4)] is proved upon applying symbolic and analytic calculations in Mathematica.