Improved domain extender for the ideal cipher

Abstract

Domain extender for the ideal cipher was firstly studied by Coron et al. (TCC 2010). The construction given by them doubles the domain. To extend the domain by a factor of t > 2, recursively applying their extender requires using the cipher exponential times, i.e. $\mathcal {O}(t^{log_{2}3})$. In this paper, we describe an improved extender which extends the domain by a factor of t with $\mathcal {O}(t)$ calls to underlying small-block blockciphers. This extender is based on a (2t − 1)-round generalized Feistel structure, and is actually a generalization of the proposal of Coron et al. We show it to be indifferentiable from an ideal cipher with tn-bit blocks. Additionally, for expansion factor t we give an attack to show that indifferentiability cannot be achieved in (2t − 2)-round case. Compared with the recursively applying strategy, the time complexity of this extender is competitive in some practical applications.

Appendices

Appendix A: Deferred Pseudocode

We formally describe the other two approaches in this section.

1.1 A.1 Pseudocode for the recursive approach

Denote the construction obtained through recursively calling Ψ₃ by ${\Psi }_{3}^{t,E[n,n]}$ where t is the expansion factor. For simplicity, we assume t = 2^h where h is an integer,⁴ assume the key length of ${\Psi }_{3}^{t,E[n,n]}$ to be 0 (the case discussed in Introduction), and only present the code for the forward computation. The code is as follows. Note that in the code, the ideal ciphers built from E[n, n] are written as private procedures. Moreover, the strings 〈0〉 and 〈1〉 are 1-bit encodings of 0 and 1, the string 〈i n d e x〉 is a $\lceil log_{2}(t^{log_{2} 3})\rceil$-bit encoding of the integer index, while 〈i〉 is a ⌈l o g ₂(2t − 1)⌉-bit encoding of i.

1.2 A.2 the 2-step approach, and the Pseudocode

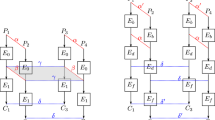
Denote the construction built through the 2-step approach by $LR_{14}^{E[n,n]}$. We also assume that the key length is 0. For t = 2l, we first build 14 length-preserving random oracles H : {0, 1}^ln → {0, 1}^ln. According to Section 5 of [8], for a fixed expansion factor t = 2l and 0 ≤ j ≤ 13, the constructions depicted in Fig. 6 give 14 such random oracles. Then the code is as follows (only include the code for the forward computation). In the code, the string 〈j⋅l + i〉 is n-bit encoding.

Fig. 6

Building length-preserving random oracle with large domain, from E[n, n]

Appendix B: Some deferred proofs

1.1 B.1 Proof for lemma 5

Wlog we consider the case of a query E[κ, t n].E n c, and the case of E[κ, t n].D e c is similar by symmetry. If E[κ, t n].E n c was made by S[t], then this was while executing the procedure F i l l i n g C h a i n, and clearly the equality holds right after the end of this procedure. Since S[t] never overwrites entries in E T, the equality holds at the end of the execution. On the other hand, if E[κ, t n].E n c(k,(x ₁,…, x _t )) was first made by $\overline {D}$, then since $\overline {D}$ is forced to call E(1,+,(x ₂,…, x _t , k), x ₁), S[t] will be triggered to call F i l l i n g C h a i n and add all the corresponding entries to E T, and the equality also holds.

1.2 B.2 Proof for Lemma 8

First, by Lemma 6 we know if $\overline {D}^{{\Sigma }_{2}(\tau (u))} = 1$, then for any $\overline {D}^{{\Sigma }_{1}(E[2n,n],S[t])}$ s.t. $ETFunc(\overline {D},{\Sigma }_{1}(E[2n,n],S[t]))=u$, $\overline {D}^{{\Sigma }_{1}(E[2n,n],S[t])}=\overline {D}^{{\Sigma }_{2}(\tau (u))} = 1$.

On the other hand, since $ETFunc(\overline {D},{\Sigma }_{1}(E[2n,n],S[t]))$ has a unique value for a fixed Σ₁-execution $\overline {D}^{{\Sigma }_{1}(E[2n,n],S[t])}$, we can partition the set of all good Σ₁ executions such that each subset corresponds to a unique $u=\mathbf {ET}\in \mathcal {T}$. Hence

$$\begin{array}{@{}rcl@{}} && Pr[ \overline{D}^{{\Sigma}_{1}(E[\kappa,tn],S[t])}\ is\ good \wedge \overline{D}^{{\Sigma}_{1}(E[\kappa,tn],S[t])} = 1] \\ &=& \sum\limits_{u\in \mathcal{T}} Pr[ ETFunc(\overline{D},{\Sigma}_{1}(E[2n,n],S[t]))=u \wedge \overline{D}^{{\Sigma}_{2}(\tau(u))} = 1] \\ &=& \sum\limits_{u\in \mathcal{T}\wedge \overline{D}^{{\Sigma}_{2}(\tau(u))} = 1} Pr[ ETFunc(\overline{D},{\Sigma}_{1}(E[2n,n],S[t]))=u] \end{array} $$

1.3 B.3 Proof for Lemma 9

To show the claim, we show that for any π ∈ R ₂:

• 1. there exists $u\in \tau (\mathcal {T})$ such that π ≅ u;

• 2. there exists at most one $u\in \tau (\mathcal {T})$ such that π ≅ u;

For the first claim, consider the Σ₁-execution $\overline {D}^{{\Sigma }_{1}}$ during which:

• 1. each time S[t] samples a random value, the value equals the corresponding value in π;

• 2. each time E[κ, n] samples a random value, the values equals the corresponding input/output value of G F S[t]^{E[(t − 1)n + κ, n](π)};

Clearly such random values are consistent, so that such a Σ₁-execution is good, and $\tau (ETFunc(\overline {D},{\Sigma }_{1}))\cong \pi$. Hence the first claim holds.

For the second claim, assume otherwise, i.e. $\exists u^{\prime }\in \tau (\mathcal {T})$ s.t. u ≠ u ^′, v ≅ u, and v ≅ u ^′. Let $v=({\pi ^{v}_{1}},\ldots ,\pi ^{v}_{2t-1})$, u = (π ₁,…, π _{2t − 1}), $u^{\prime }=(\pi ^{\prime }_{1},\ldots ,\pi ^{\prime }_{2t-1})$, and let the preimages of u and u ^′ be $\mathbf {ET}\in \mathcal {T}$ and $\mathbf {ET}^{\prime }\in \mathcal {T}$. Consider any two executions $\overline {D}^{{\Sigma }_{1}(E[\kappa ,tn],S[t])}$ and $\overline {D}^{{\Sigma }_{1}(E[\kappa ,tn],S[t])'}$ such that:

• 1. $ETFunc(\overline {D}, {\Sigma }_{1}(E[\kappa ,tn],S[t]))=\mathbf {ET}=(ET_{1},\ldots ,ET_{2t-1})$,

• 2. $ETFunc(\overline {D}, {\Sigma }_{1}(E[\kappa ,tn],S[t])')=\mathbf {ET}^{\prime }=(ET^{\prime }_{1},\ldots ,ET^{\prime }_{2t-1})$.

We show $Transcript(\overline {D},{\Sigma }_{1}(E[\kappa ,tn],S[t]))=Transcript(\overline {D},{\Sigma }_{1}(E[\kappa ,tn],S[t])')$ to show that the query-answer pairs generated in the two executions are exactly the same, so that E T = E T ^′ and u = u ^′. Assume that in the two executions, the answers for the first j − 1 queries equal correspondingly, and consider the j-th query-answer tuple q a _j and $qa_{j}^{\prime }$ in the two transcripts. Since both $\overline {D}$ and S[t] (excluding the procedure E ⁱⁿ) are deterministic, the procedure fields of q a _j and $qa^{\prime }_{j}$ are equal. We argue that the answer fields of them are the same. For the following cases:

• If the procedure field is E ⁱⁿ and the query is (i, δ, k, z), then the answers in the two executions are equal since they equal the corresponding values in E T and E T ^′, and $ET_{i}(\delta ,K,z)=\pi _{i}(\delta ,K,z)={\pi ^{v}_{i}}(\delta ,K,z)=\pi _{i}^{\prime }(\delta ,K,z)=ET_{i}^{\prime }(\delta ,K,z)$.

• If the procedure field is E n c or D e c, following the same line as in the proof of Lemma 6 we can show that the answers are the same.

Hence $Transcript(\overline {D},{\Sigma }_{1}(E[\kappa ,tn],S[t]))=Transcript(\overline {D},{\Sigma }_{1}(E[\kappa ,tn],S[t])')$, and u = E T = E T ^′ = u ^′, contradicting the assumption.

Then, with the two claims at hand, we have:

$$\begin{array}{@{}rcl@{}} \sum\limits_{v\in R_{2}\wedge \overline{D}^{{\Sigma}_{2}(v)} = 1} Pr_{\pi}[\pi=v] &=& \sum\limits_{v\in R_{2} \wedge\overline{D}^{{\Sigma}_{2}(v)} = 1\wedge \exists u\in\tau(\mathcal{T})\ s.t.\ v\cong u} Pr_{\pi}[\pi= v] \\ &=& \sum\limits_{u\in\tau(\mathcal{T}) \wedge\overline{D}^{{\Sigma}_{2}(u)} = 1 } \left[ \sum\limits_{v\in R_{2} \wedge v\cong u } Pr_{\pi}[\pi= v] \right] \\ &=& \sum\limits_{u\in\tau(\mathcal{T}) \wedge\overline{D}^{{\Sigma}_{2}(u)} = 1} Pr_{\pi}[\pi\cong u] \end{array} $$