Secure communication via an energy-harvesting untrusted relay with imperfect CSI

Abstract

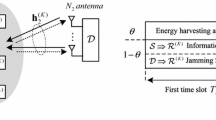
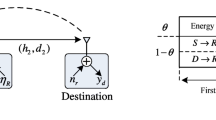
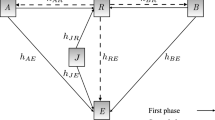
This paper studies the secure communication of an energy-harvesting system in which a source communicates with a destination via an amplify-and-forward (AF) untrusted relay. The relay uses the power-splitting policy to harvest energy from wireless signals. The source is equipped with multiple antennas and uses transmit antenna selection (TAS) and maximum ratio transmission (MRT) to enhance the harvested energy at the relay; for performance comparison, random antenna selection (RAS) is examined. The relay and destination are single-antenna nodes. To create a positive secrecy capacity, destination-assisted jamming is deployed. Because the use of multiple antennas can cause the imperfect channel state information (CSI), the channel between the source and the relay is examined in two cases: perfect CSI and imperfect CSI. To evaluate the secrecy performance, analytical expressions for the secrecy outage probability (SOP) and the average secrecy capacity (ASC) for the TAS, MRT, and RAS schemes are derived. Moreover, a high-power approximation for the SOP is presented. The accuracy of the analytical results is verified by Monte Carlo simulations. The results show the benefit of using multiple antennas in improving the secrecy performance. Specifically, MRT performs better than TAS, and both of them outperform RAS. Moreover, the results provide valuable insight into the effects of various system parameters, such as the channel correlation coefficient, energy-harvesting efficiency, secrecy rate threshold, power-splitting ratio, transmit powers, and locations of the relay, on the secrecy performance.

Appendices

Appendix A: Proof of Proposition 1

Let x ₁,…,x _N be N exponential RVs with a rate parameter λ, and the PDF and CDF of x _n , 1 ≤ n ≤ N, are respectively given by

$$\begin{array}{@{}rcl@{}} f(\lambda ;x) & =& \lambda e^{- \lambda x}, \end{array} $$

(33)

$$\begin{array}{@{}rcl@{}} F(\lambda ;x)& =& 1 - e^{- \lambda x}. \end{array} $$

(34)

Let us define Y = max{x ₁,…,x _N } and $Z={\sum }_{n=1}^{N} x_{n}$. The CDFs of Y and Z are respectively given by

$$\begin{array}{@{}rcl@{}} {F_{Y}}\left( {\lambda ,N;x} \right) &\,=\,& F{\left( {\lambda ;x} \right)^{N}} \,=\, 1 \,+\, \sum\limits_{n = 1}^{N} \binom{N}{n} {\left( { - 1} \right)^{n}}{e^{- n\lambda x}}, \end{array} $$

(35)

$$\begin{array}{@{}rcl@{}} {F_{Z}}\left( {\lambda ,N;x} \right) &=& 1 - {e^{- \lambda x}}\sum\limits_{n = 0}^{N - 1} {\frac{{{{\left( {\lambda x} \right)}^{n}}}}{{n!}}}. \end{array} $$

(36)

Next, we rewrite Eq. 12 as

$$ \text{SOP} \,=\, 1 - \int\limits_{{{\bar x}_{1}}}^{+ \infty} {\left( {1 \,-\, {F_{{X_{1}}}}\left( {{\lambda_{1}},N;\tfrac{{\beta - 1}}{{\zeta \left( {1 - \theta} \right){\rho_{s}}{\Xi} \left( {x;\beta} \right)}}} \right)} \right)} {f_{{X_{2}}}}\left( {{\lambda_{2}};x} \right)dx. $$

(37)

where ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ are the cumulative distribution function (CDF) of X ₁ and the probability density function (PDF) of X ₂, respectively.

1.1 A.1 Calculation for SOP_RAS

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 37 with F(λ ₁; x) and f(λ ₂; x), respectively, we obtain Eq. 13.

1.2 A.2 Calculation for SOP_TAS

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 37 with F _Y (λ ₁,N; x) and f(λ ₂; x), respectively, we obtain Eq. 14.

1.3 A.3 Calculation for SOP_MRT

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 37 with F _Z (λ ₁,N; x) and f(λ ₂; x), respectively, we obtain Eq. 15.

Finally, Proposition 1 is proved.

Appendix B: Proof of Proposition 2

1.1 B.1 Calculation for case of perfect CSI (ζ = 1)

In this case, we have $\mu =1, {\Xi } \left ({x;\beta } \right ) \approx \frac {x}{{x + \kappa } }$, and ${\bar x_{1}} \approx \sqrt {\frac {{\beta } }{{\eta \theta {\rho _{d}}}}}$. Therefore, Eq. 12 can be approximated as

$$ \text{SOP} = 1 - \Pr \left( {{X_{1}} > {{\bar x}_{3}}|{X_{2}} > {{\bar x}_{1}}} \right) \approx {F_{{X_{2}}}}\left( {{\lambda_{2}};{{\bar x}_{1}}} \right), $$

(38)

where ${\bar x_{3}} = \frac {{\left ({\beta - 1} \right )}}{{\left ({1 - \theta } \right ){\rho _{s}}}}\left ({1 + \frac {\kappa } {{{X_{2}}}}} \right )$, and the approximation in Eq. (38) is obtained due to the fact that $\mathop {\lim } \limits _{\left ({{\rho _{s}},{\rho _{d}}} \right ) \to \left ({\infty ,\infty } \right )} \frac {{{{\bar x}_{3}}}}{{{{\bar x}_{1}}}} = 0$.

Using the series representation of the exponential function given in [15, Eq. (1.211.1)], we can prove (16).

1.2 B.2 Calculation for case of perfect CSI (0 < ζ < 1)

In this case, we have $\mu \approx {\mu _{0}}: = \left ({1 - \zeta } \right )\left ({1 - \theta } \right )\tfrac {{{\rho _{s}}}}{{{\lambda _{1}}}}$ and ${\Xi } \left ({x;\beta } \right ) \approx \frac {1}{\mu } - \frac {\beta } {{\left ({1 - \theta } \right ){\rho _{d}}{X_{2}} + \mu } }$. Therefore, $\frac {1}{{\Xi \left ({x;\beta } \right )}}$ can be approximated by

$$ \frac{1}{{\Xi \left( {x;\beta} \right)}} \approx \mu \left( {1 + \frac{{\left( {1 - \zeta} \right)\omega \beta} }{{{\lambda_{1}}\left( {{X_{2}} - {{\bar x}_{2}}} \right)}}} \right). $$

(39)

Then, the asymptotic functions for the SOP are calculated by

$$\begin{array}{@{}rcl@{}} \text{SOP}^{\infty} &\,=\,& 1 \,-\, \Pr \left( {X_{1}} \!>\! \tfrac{{\bar x}_{2}}{{\omega \zeta} }\left( 1 \,+\, \tfrac{{\left( {1 - \zeta} \right)\omega \beta} }{{{\lambda_{1}}\left( {{X_{2}} - {{\bar x}_{2}}} \right)}} \right)|{X_{2}} \!>\! {{\bar x}_{2}} \right) \\ &\,=\,& 1 \,-\, \int\limits_{{\bar x}_{2}}^{\infty} \left( 1 \,-\, {F_{{X_{1}}}}\left( {{\lambda_{1}},N;\tfrac{{\bar x}_{2}}{{\omega \zeta} } \left( {1 \,+\, \tfrac{\left( {1 - \zeta} \right)\omega \beta} {{\lambda_{1}}\left( {x - {{\bar x}_{2}}} \right)}} \right)} \right) \right) {f_{{X_{2}}}}\left( {{\lambda_{2}};x} \right)dx. \\ \end{array} $$

(40)

Let us define $t=x-\bar x_{2}$, Eq. 40 can be rewritten as

$$ \text{SOP}^{\infty} \,=\, 1 - \int\limits_{0}^{\infty} \left( 1 \,-\, F_{{X_{1}}}\left( {{\lambda_{1}},N;\tfrac{{\bar x}_{2}}{\omega \zeta} \left( {1 \,+\, \tfrac{{\left( {1 - \zeta} \right)\omega \beta} }{{{\lambda_{1}}t}}} \right)} \right) \right) {f_{{X_{2}}}}\left( {{\lambda_{2}};t \,+\, {{\bar x}_{2}}} \right)dt. $$

(41)

1.2.1 B.2.1 Calculation for $\textup {SOP}_{\textup {RAS}}^{\infty }$

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and $f_{{X_{2}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 41 with F(λ ₁; x) and f(λ ₂; x), respectively, we have

$$ \text{SOP}^{\infty} = 1 - {\lambda_{2}}{e^{- \frac{{{\lambda_{1}}{{\bar x}_{2}}}}{{\omega \zeta} } - {\lambda_{2}}{{\bar x}_{2}}}}\int\limits_{0}^{\infty} {e^{- \frac{ {{\bar x}_{2}} \left( 1 - \zeta \right) \beta } {{\zeta} t} - {\lambda_{2}}t}} dt. $$

(42)

With the help of [15, Eq. (3.471.9)], Eq. 42 can be expressed as Eq. 17.

1.2.2 B.2.2 Calculation for $\textup {SOP}_{\textup {TAS}}^{\infty }$

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 41 with F _Y (λ ₁,N; x) and f(λ ₂; x), respectively, and using the same step in the calculation for SOPRAS∞, we obtain Eq. 18.

1.2.3 B.2.3 Calculation for $\textup {SOP}_{\textup {MRT}}^{\infty }$

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 41 with F _Z (λ ₁,N; x) and f(λ ₂; x), respectively, and using the same step in the calculation for SOPRAS∞, we obtain Eq. 19.

Finally, Proposition 2 is proved.

Appendix C: Proof of Proposition 3

1.1 C.1 Calculation for the RAS scheme

Using the PDFs of X ₁ and X ₂ for the RAS scheme given by f(λ ₁; x) and f(λ ₂; x), respectively, and [15, Eq.(4.352.1)], $\mathcal {J}_{1}$ and $\mathcal {J}_{2}$ for the RAS scheme are calculated as

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{1}^{{\text{RAS}}} &=& {\Psi} \left( 1 \right) - \ln \left( {{\lambda_{1}}} \right), \end{array} $$

(43)

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{2}^{{\text{RAS}}} &=& {\Psi} \left( 1 \right) - \ln \left( {{\lambda_{2}}} \right) \end{array} $$

(44)

Moreover, using the PDFs of X2 and [15, Eq.(4.337.1)], $\mathcal {J}_{3}$ for the RAS scheme is calculated as

$$ \mathcal{J}_{3}^{{\text{RAS}}} = \ln \left( \kappa \right) - {e^{\frac{{{\lambda_{2}}\kappa} }{\mu}}}Ei\left( { - \tfrac{{{\lambda_{2}}\kappa} }{\mu} } \right). $$

(45)

Substituting Eqs. 43, 44, and 45 into Eq. 22 yields (23).

1.2 C.2 Calculation for the TAS scheme

According to [18], the PDF of Y defined in Appendix A is given by

$$ {f_{Y}}\left( {\lambda ,N;x} \right) = Nf\left( {\lambda ;x} \right)F{\left( {\lambda ;x} \right)^{N-1}}. $$

(46)

Using the PDF of X ₁ for the TAS scheme given by f _Y (λ ₁,N; x) and [15, Eq.(4.352.1)], $\mathcal {J}_{1}$ for the TAS scheme is calculated as

$$ \mathcal{J}_{1}^{{\text{TAS}}} = N\sum\limits_{n = 0}^{N - 1} \binom{N-1}{n} \frac{{{{\left( { - 1} \right)}^{n}}}}{{{n + 1}}}\left( {\Psi \left( 1 \right) - \ln \left( {\left( {n + 1} \right){\lambda_{1}}} \right)} \right). $$

(47)

Using the fact that $N\sum \limits _{n = 0}^{N - 1} \binom {N-1}{n} \frac {{{{\left ({ - 1} \right )}^{n}}}}{{\left ({n + 1} \right )}} = 1$, we can rewrite Eq. 47 as

$$ \mathcal{J}_{1}^{{\text{TAS}}} = {\Psi} \left( 1 \right) - N\sum\limits_{n = 0}^{N - 1} \binom{N-1}{n} \frac{{{{\left( { - 1} \right)}^{n}}}}{{ {n + 1}} }\ln \left( {\left( {n + 1} \right){\lambda_{1}}} \right). $$

(48)

Because $\mathcal {J}_{2}$ and $\mathcal {J}_{3}$ for the TAS scheme are the same as for the RAS scheme, Eq. 24 is obtained by substituting Eqs. 44, 45 and 48 into Eq. 22.

1.3 C.3 Calculation for the MRT scheme

According to [8], the PDF of Z defined in Appendix A is given by

$$ {f_{Z}}\left( {\lambda ,N;x} \right) = \frac{{{\lambda^{N}}{x^{N - 1}}}}{{\Gamma \left( N \right)}}{e^{- \lambda x}}. $$

(49)

Using the PDF of X ₁ for the MRT scheme given by f _Z (λ ₁,N; x) and [15, Eq.(4.352.1)], $\mathcal {J}_{1}$ for the MRT scheme is calculated as

$$ \mathcal{J}_{1}^{{\text{MRT}}} = \psi \left( N \right) - \ln \left( {{\lambda_{1}}} \right). $$

(50)

Because $\mathcal {J}_{2}$ and $\mathcal {J}_{3}$ for the MRT scheme are the same as for the RAS scheme, Eq. 25 is obtained by substituting Eqs. 44, 45, and 50 into Eq. 22.

Appendix D: Proof of Proposition 4

From Eq. 7, the PDF of γ _r is calculated as

$$\begin{array}{@{}rcl@{}} {F_{{\gamma_{r}}}}\left( \gamma \right) &\,=\,& \Pr \left( {{\gamma_{r}} < \gamma} \right)\\ &\,=\,& \int\limits_{0}^{\infty} {{F_{{X_{1}}}}\left( {{\lambda_{1}},N;\tfrac{{\gamma \left( {\left( {1 - \theta} \right){\rho_{d}}x + \mu} \right)}}{{\zeta \left( {1 - \theta} \right){\rho_{s}}}}} \right)} {f_{{X_{2}}}}\left( {{\lambda_{2}};x} \right)dx.\\ \end{array} $$

(51)

1.1 D.1 Calculation for the RAS scheme

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 50 with F(λ ₁; x) and f(λ ₂; x), respectively, Eq. 50 can be expressed as

$$ {F_{{\gamma_{r}}}}\left( \gamma \right) = 1 - {\left( {\frac{{{\lambda_{1}}\gamma} }{{{\lambda_{2}}\zeta \omega} } + 1} \right)^{- 1}}{e^{- \frac{{{\lambda_{1}}\gamma \mu} }{{\zeta \left( {1 - \theta} \right){\rho_{s}}}}}}. $$

(52)

Substituting Eqs. 50 into Eq. 26, we have the following:

$$ \bar{\mathcal{C}}_{r} = \frac{1}{{\ln \left( 2 \right)}}\int\limits_{0}^{\infty} \left( \tfrac{\lambda_{1} \gamma}{\lambda_{2} \zeta \omega} + 1 \right)^{-1} \left( {1 + \gamma} \right)^{-1} {e^{- \frac{{{\lambda_{1}}\gamma \mu} }{{\zeta \left( {1 - \theta} \right){\rho_{s}}}}}}d\gamma. $$

(53)

In the case of λ ₁ ≠ λ ₂ ζ ω, $\left ({\tfrac {{{\lambda _{1} \gamma }}}{{{\lambda _{2}}\zeta \omega } } \,+\, 1} \right )^{-1} ({1 \,+\, \gamma } )^{-1}$ can be expressed as ${\left ({1 \,-\, \tfrac {{{\lambda _{1}}}}{{{\lambda _{2}}\zeta \omega } }} \right )^{- 1}}\left ({{{\left ({\gamma \,+\, 1} \right )}^{- 1}} \,-\, {{\left ({\gamma \,+\, {} \tfrac {{{\lambda _{2}}\zeta \omega } }{{{\lambda _{1}}}}} \right )}^{- 1}}} \right )$. Then, using [15, Eq.(3.383.10)], we obtain Eq. 27. In the case of λ ₁ = λ ₂ ζ ω, we obtain Eq. 28 with the help of [15, Eq. (3.353.2)].

1.2 D.2 Calculation for the TAS scheme

The result for the TAS scheme can be obtained by replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 50 with F _Y (λ ₁,N; x) and f(λ ₂; x), respectively, and using the same step as in Appendix D.1.

1.3 D.3 Calculation for the MRT scheme

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 50 with F _Z (λ ₁,N; x) and f(λ ₂; x), respectively, and using [15, Eq.(8.350.2)], Eq. 50 can be expressed as

$$\begin{array}{@{}rcl@{}} {F_{{\gamma_{r}}}}\left( \gamma \right) &\,=\, &1 \,-\, {\lambda_{2}}{e^{- \frac{{{\lambda_{1}}\mu \gamma} }{{\zeta \left( {1 - \theta} \right){\rho_{s}}}}}}\sum\limits_{n = 0}^{N - 1} {\frac{1}{{n!}}{{\left( {\frac{{{\lambda_{1}}\gamma} }{{\zeta \omega} }} \right)}^{n}}} \\ &&\!\times\! \sum\limits_{k = 0}^{n} \binom{n}{k} {\left( {\frac{\mu} {{\left( {1 \,-\, \theta} \right){\rho_{d}}}}} \right)^{n - k}}\frac{{\Gamma \left( {k \,+\, 1} \right)}}{{{{\left( {\frac{{{\lambda_{1}}\gamma} }{{\zeta \omega} } \,+\, {\lambda_{2}}} \right)}^{k + 1}}}}. \end{array} $$

(54)

Substituting Eq. 53 into Eq. 26, we have the following:

$$\begin{array}{@{}rcl@{}} \bar {\mathcal{C}}_{r} &= &\frac{{{\lambda_{2}}}}{{\ln \left( 2 \right)}}\sum\limits_{n = 0}^{N - 1} {\frac{1}{{n!}}{{\left( {\frac{{{\lambda_{1}}}}{{\zeta \omega} }} \right)}^{n}}} \sum\limits_{k = 0}^{n} \binom{n}{k} {\left( {\frac{\mu} {{\left( {1 - \theta} \right){\rho_{d}}}}} \right)^{n - k}} \\ &&\times {\Gamma} \left( {k + 1} \right)\int\limits_{0}^{\infty} {{\gamma^{n}}} \mathcal{I}\left( \gamma \right){e^{- \frac{{{\lambda_{1}}\mu \gamma} }{{\zeta \left( {1 - \theta} \right){\rho_{s}}}}}}d\gamma , \end{array} $$

(55)

where $\mathcal {I}\left (\gamma \right ) = {\left ({1 + \gamma } \right )^{- 1}}{\left ({\tfrac {{{\lambda _{1}}}}{{\zeta \omega } }\gamma + {\lambda _{2}}} \right )^{- k - 1}}$.

In the case of λ ₁≠λ ₂ ζ ω, $\mathcal {I}\left (\gamma \right )$ can be decomposed using partial fraction decomposition as follows.

$$ \mathcal{I}\left( \gamma \right) = \frac{{{A_{0}}}}{{\left( {1 + \gamma} \right)}} + \sum\limits_{i = 1}^{k + 1} {\frac{{{A_{i}}}}{{{{\left( {\frac{{{\lambda_{1}}}}{{\zeta \omega} }\gamma + {\lambda_{2}}} \right)}^{i}}}}}. $$

(56)

Substituting Eq. 55 into Eq. 54 and using [15, Eq.(3.383.10) and Eq.(9.211.4)], we obtain Eq. 31.

In the case of λ ₁ = λ ₂ ζ ω, $\mathcal {I}\left (\gamma \right ) = {\left ({\tfrac {{\zeta \omega } }{{{\lambda _{1}}}}} \right )^{k + 1}}{({\gamma + 1})^{- k - 2}}$. Then, with the help of [15, Eq. (9.211.4)], we obtain Eq. 32.