A decentralized coordination mechanism for integrated production–transportation–inventory problem in the supply chain using Lagrangian relaxation

Abstract

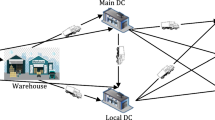
This paper is concerned with integrated production, inventory and transportation planning problems directly related to the supply chain management. We establish a Lagrangian based coordination mechanism within the context of the decentralized planning approach. In addition, we demonstrate that dual prices obtained by the described approach might provide enough accuracy in case of sudden changes, such as in a customer’s demand, and thus they could assist agents to find new solutions. Computational results show that the proposed mechanism is able to help organizations to facilitate collaboration, improve business agility and meet business goals.

Appendix

We consider the linear program

$$ \begin{gathered} ({\mathbf{P1}})\quad \min \quad {\mathbf{c}}^T {\mathbf{x}} + {\mathbf{d}}^T {\mathbf{y}} \hfill \\ {\text{s}} . {\text{t}} .\quad {\mathbf{Ax}} + {\mathbf{By}} \ge {\mathbf{b}} \hfill \\ {\mathbf{A}}_ 1{\mathbf{x}} \ge {\mathbf{b}}_ 1\hfill \\ {\mathbf{B}}_ 1{\mathbf{y}} \ge {\mathbf{b}}_ 2\hfill \\ {\mathbf{x}} \in X,\;{\mathbf{y}} \in Y \hfill \\ \end{gathered} $$

and rewrite it in the equivalent form

$$ \begin{gathered} ({\mathbf{P2}})\quad \min \quad {\mathbf{c}}^T {\mathbf{x}} + {\mathbf{d}}^T {\mathbf{y}} \hfill \\ {\text{s}} . {\text{t}} .\quad {\mathbf{Ax}} + {\mathbf{Bz}} \ge {\mathbf{b}} \hfill \\ {\mathbf{A}}_ 1{\mathbf{x}} \ge {\mathbf{b}}_ 1\hfill \\ {\mathbf{B}}_ 1{\mathbf{y}} \ge {\mathbf{b}}_ 2\hfill \\ {\mathbf{x}} \in X,\;{\mathbf{y}} \in Y,\;{\mathbf{z}} \in Y \hfill \\ - {\mathbf{y}} + {\mathbf{z}} = 0. \hfill \\ \end{gathered} $$

We will assume that X and Y are polytopes, i.e., closed and bounded polyhedra. Applying Lagrangian relaxation to the equality constraints, the problem separates into two Lagrangian subproblems:

$$ \begin{gathered} {\text{Val}}_1 ({\mathbf{v}})\quad \min \quad {\mathbf{c}}^T {\mathbf{x}} + {\mathbf{v}}^T {\mathbf{z}} \hfill \\ {\text{s}} . {\text{t}} .\quad {\mathbf{Ax}} + {\mathbf{Bz}} \ge {\mathbf{b}} \hfill \\ {\mathbf{A}}_ 1{\mathbf{x}} \ge {\mathbf{b}}_ 1\hfill \\ {\mathbf{x}} \in X,\;{\mathbf{z}} \in Y \hfill \\ \end{gathered} $$

and

$$ \begin{gathered} {\text{Val}}_2 ({\mathbf{v}})\quad \min \quad ({\mathbf{d}} - {\mathbf{v}})^T {\mathbf{y}} \hfill \\ {\text{s}} . {\text{t}} .\quad {\mathbf{By}} \ge {\mathbf{b}}_ 2\hfill \\ {\mathbf{y}} \in Y. \hfill \\ \end{gathered} $$

The Lagrangian dual problem is then ${\max _{\mathbf{v}} \min _{({\mathbf{x}},{\mathbf{z}},{\mathbf{y}})} L({\mathbf{x}},{\mathbf{z}},{\mathbf{y}},{\mathbf{v}})},$ where ${L({\mathbf{x}},{\mathbf{z}},{\mathbf{y}},{\mathbf{v}}) = {\text{val}}_1 ({\mathbf{v}}) + {\mathbf{val}}_2 ({\mathbf{v}})}.$ Suppose we solve it using the simple sub-gradient algorithm, that is, by creating a sequence ${\{ {\mathbf{v}}(k)\} ,}$ where ${{\mathbf{v}}(k + 1) = {\mathbf{v}}(k) + \alpha (k){\mathbf{g}}(k)},$ ${k \ge 1 ,\,{\mathbf{g}}(k) = {\mathbf{z}}(k) + {\mathbf{y}}(k)}$ with (x(k), z(k)) and y(k) being the subproblem solutions, and α(k) ≥ 0 satisfying α(k) → 0 and $\sum\nolimits_{k = 1}^\infty {\alpha (k) = \infty } .$ Then ${\{ {\mathbf{v}}(k)\} \to {\mathbf{v}}^* },$ where v ^* is an optimal dual solution.

Next we introduce the weights

$$ {\beta (N;k) = \frac{{\alpha (k)}}{{\sum\nolimits_{i = 1}^N {\alpha (i)} }}} $$

and define the weighted sequence, ${\{ {\mathbf{x}} (N ) ,{\mathbf{z}} (N ) ,{\mathbf{y}} (N )\} ,}$ where

$$ {{\mathbf{x}}(N) = \sum\limits_{k = 1}^N {\beta (N;k){\mathbf{x}}(k)} ,} $$

$$ {{\mathbf{z}}(N) = \sum\limits_{k = 1}^N {\beta (N;k){\mathbf{z}}(k),} } $$

$$ {{\mathbf{y}}(N) = \sum\limits_{k = 1}^N {\beta (N;k){\mathbf{y}}(k).} } $$

Clearly, by the convexity of X and Y and since, ${\sum\nolimits_{k = 1}^N {\beta (N;k)} = 1},\,\beta (N;k) \ge 0{\;\{ {\mathbf{x}}({N})\} \in {X}},\,\{ {\mathbf{z}} ({N})\} \in Y$ and $\left\{ {{\mathbf{y}} ({N})} \right\} \in Y.$ Hence, {x(N) z(N) y(N)} has an accumulation point $({\hat{\mathbf{x}}},{\hat{\mathbf{z}}},{\hat{\mathbf{y}}})$ X × Y × Y. Moreover, let g(N) be the subgradient at ${\{ {\mathbf{x}} ({N}),{\mathbf{z}} (N),{\mathbf{y}} ({N})\} },$ then ${{\mathbf{g}} (N )= \sum\limits_{k = 1}^N {\beta (N;k)} ({\mathbf{z}}(k) - {\mathbf{y}}(k))}$ by the definition of ${\{ {\mathbf{x}} ({N}),{\mathbf{z}} ({N}),{\mathbf{y}} ({N})\} .}$ Then, since, ${{\mathbf{v}}(k + 1) = {\mathbf{v}}(k) + \alpha (k){\mathbf{g}}(k),\,\;k \ge 1},$ we have ${\sum\nolimits_{k = 1}^N {\beta (N;k)} {\kern 1pt} {\mathbf{g}}(k) = \frac{{{\mathbf{v}}(k + 1) - {\mathbf{v}}(1)}}{{\sum\nolimits_{i = 1}^N {\alpha (i)} }}}$ which approaches 0 since $\left\{ {{\mathbf{v}}(k)} \right\} \to {\mathbf{v}}^*$ as $k \to \infty$ and ${\sum\nolimits_{i = 1}^N {\alpha (i)} \to \infty }$ as N → ∞. Thus, ${\{ {\mathbf{g}}(N)\} \to 0}$ and consequently the accumulation point of the sequence ${\{ {\mathbf{x}}(N),{\mathbf{z}}(N),{\mathbf{y}}(N)\} }$ solves P2 implying that $({\hat{\mathbf{x}}},{\hat{\mathbf{y}}})$ solves P1. This proves Proposition 2.