Pricing and quality competition for substitutable green products with a common retailer

Abstract

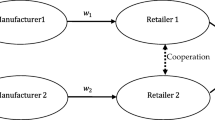
This study explores two competing manufacturers’ green investment decisions with different market sizes in selling price- and green-level-differentiated substitutable green products through a retailer. Five game structures are considered in examining the impacts of power structures on the optimal price and green level decisions and the corresponding equilibrium decisions. A two-way revenue-sharing contract is proposed from the perspective of improving the performance of each member. Numerical experiments are conducted to illustrate the results and gain managerial insights for green product manufacturing and selling in a competitive market. The results demonstrate that the two competing manufacturers need to cooperate rather than compete if cross-price elasticity or the difference between market potentials is too high. In this scenario, the equilibrium outcome can outperform the overall green supply chain’s performance compared to those achieved under the Bertrand or Nash game. The retailer also receives benefits. Due to a higher variation in market size and price sensitivity, the retailer may receive higher profits under the manufacturer’s leadership and vice versa. Therefore, the results contradict the common consensus. Although greening levels remain higher if the retailer dominates or the members have equal power, every member can receive suboptimal profits in these scenarios. It is found that a two-way revenue-sharing contract mechanism based on product market sizes can improve the overall green supply chain’s performance and allocate profit surplus arbitrarily.

Appendices

Appendix

A Optimal decision in scenario MB

The optimal solution for the retailer’s optimization problem defined in Eq. (1) is obtained by solving $\frac{\partial \varPi _{r}^{MB}}{\partial p_1^{MB}}=0$ and $\frac{\partial \varPi _{r}^{MB}}{\partial p_2^{MB}}=0$, simultaneously. After simplification, market prices are obtained as

• $p_1^{MB}=\frac{a+w_1^{MB}(1- \beta ^2)+a k \beta +\gamma \theta _1^{MB}-\beta \delta \theta _1^{MB}+\beta \gamma \theta _2^{MB}-\delta \theta _2^{MB}}{2(1- \beta ^2)}$

• $p_2^{MB}=\frac{w_2^{MB}(1- \beta ^2)+a (k+\beta )+\beta \gamma \theta _1^{MB}-\delta \theta _1^{MB}+\gamma \theta _2^{MB}-\beta \delta \theta _2^{MB}}{2(1- \beta ^2)}$

From the above expressions, one can find that wholesale prices do not directly affect the other products’ market prices, but the GLs make. To verify concavity, we computed the Hessian matrix for the retailer’s profit($H_r^{MB}$) as follows:

$$\begin{aligned} H_r^{MB} = \left| \begin{array}{cc}\frac{\partial ^2 \varPi _{r}^{MB}}{\partial {p_1^{MB}}^2} &{} \frac{\partial ^2 \varPi _{r}^{MB}}{\partial p_1^{MB}\partial p_2^{MB}} \\ \frac{\partial ^2 \varPi _{r}^{MB}}{\partial ^2 p_1^{MB}\partial p_2^{MB}} &{} \frac{\partial ^2 \varPi _{r}^{MB}}{\partial {p_2^{MB}}^2} \\ \end{array} \right| = \left| \begin{array}{cc}-2 &{} 2\beta \\ 2\beta &{} 2\\ \end{array} \right| =4(1-\beta ^2)>0 \end{aligned}$$

Therefore, the profit function for the retailer is concave. By substituting optimal responses in Eqs. (2) and (3), profit functions for manufacturers are obtained as follows:

• $\varPi _{m1}^{MB}=\frac{a w_1^{MB}-{w_1^{MB}}^2-2 \eta {\theta _1^{MB}}^2+w_1^{MB} (w_2^{MB} \beta +\gamma \theta _1^{MB}-\delta \theta _2^{MB}))}{2}$

• $\varPi _{m2}^{MB}=\frac{(a k+\gamma {\theta _2^{MB}}) w_2^{MB}-w_2^{MB} (w_2^{MB}-w_1^{MB} \beta +\delta \theta _1^{MB}) -2 \eta {\theta _2^{MB}}^2}{2}$

Therefore, optimal wholesale prices and GLs for the two manufacturers can be obtained by solving $\frac{\partial \varPi _{m1}^{MB}}{\partial w_1^{MB}} = 0$; $\frac{\partial \varPi _{m1}^{MB}}{\partial \theta _1^{MB}} = 0$; $\frac{\partial \varPi _{m2}^{MB}}{\partial w_2^{MB}} = 0$;$\frac{\partial \varPi _{m2}^{MB}}{\partial \theta _2^{MB}} = 0$, simultaneously. The simplified values of the solution are presented in Table  3.

Profit function for each manufacturer are also concave because the value of the determinant of the Hessian matrix($H_{mi}^{MB}$) is obtained as follows:

$$\begin{aligned} H_{mi}^{MB} = \left| \begin{array}{cc}\frac{\partial ^2 \varPi _{mi}^{MB}}{\partial {w_i^{MB}}^2} &{} \frac{\partial ^2 \varPi _{mi}^{MB}}{\partial w_i^{MB}\partial \theta _i^{MB}} \\ \frac{\partial ^2 \varPi _{mi}^{MB}}{\partial w_i^{MB}\partial \theta _i^{MB}} &{} \frac{\partial ^2\varPi _{mi}^{MB}}{\partial {\theta _i^{MB}}^2} \\ \end{array} \right| = \left| \begin{array}{cc}-1 &{} \frac{\gamma }{2} \\ \frac{\gamma }{2} &{} -2\eta \\ \end{array} \right| =\frac{8\eta -\gamma ^2}{4} \end{aligned}$$

Therefore, profit functions for each manufacturer are also concave if $8\eta >\gamma ^2$. Moreover, from the simplified values of profit functions presented in Table 3, one can find that the condition is necessary for each manufacturer to receive non-negative profits.

B Optimal decision in scenario RB

First, the two manufacturers’ decisions are derived by substituting $m_i^{RB}=p_i^{RB}-w_i^{RB}$ in Eqs. (2) and (3); these represent the per-unit profit margin for product i. Therefore, wholesale prices and GLs are obtained by solving $\frac{\partial \varPi _{m1}^{RB}}{\partial w_1^{RB}}=0$; $\frac{\partial \varPi _{m1}^{RB}}{\partial \theta _1^{RB}}=0$; $\frac{\partial \varPi _{m2}^{RB}}{\partial w_2^{RB}}=0$; and $\frac{\partial \varPi _{m2}^{RB}}{\partial \theta _2^{RB}}=0$, simultaneously. After simplification, wholesale prices and GLs are obtained as follows:

• $w_1^{RB}=\frac{2 \eta ((a-m_1^{RB}+m_2^{RB} \beta ) (4 \eta -\gamma ^2)+(a k-m_2^{RB}+m_1^{RB} \beta ) (2 \beta \eta -\gamma \delta ))}{\varDelta _{rb}}$

• $w_2^{RB}=\frac{2 \eta ((a k-m_2^{RB}+m_1^{RB} \beta )(4 \eta -\gamma ^2)+(a-m_1^{RB}+m_2^{RB} \beta ) (2 \beta \eta -\gamma \delta ))}{\varDelta _{rb}}$

• $\theta _1^{RB}=\frac{\gamma ((a-m_1^{RB}+m_2^{RB} \beta ) (4 \eta -\gamma ^2)+(a k-m_2^{RB}+m_1^{RB} \beta ) (2 \beta \eta -\gamma \delta ))}{\varDelta _{rb}}$

• $\theta _2^{RB}=\frac{\gamma ((a k-m_2^{RB}+m_1^{RB} \beta )(4 \eta -\gamma ^2)+(a-m_1^{RB}+m_2^{RB} \beta ) (2 \beta \eta -\gamma \delta ))}{\varDelta _{rb}}$

To verify the concavity of the profit function for each manufacturer, we compute the value of the determinant of the Hessian matrix ($H_{mi}^{RB}$) as follows:

$$\begin{aligned} H_{mi}^{RB} = \left[ \begin{array}{cc}\frac{\partial ^2 \varPi _{mi}^{RB}}{\partial {w_i^{RB}}^2} &{} \frac{\partial ^2\varPi _{mi}^{RB}}{\partial w_i^{RB}\partial \theta _i^{RB}} \\ \frac{\partial ^2\varPi _{mi}^{RB}}{\partial w_i^{RB}\partial \theta _i^{RB}} &{} \frac{\partial ^2\varPi _{mi}^{RB}}{\partial {\theta _i^{RB}}^2} \\ \end{array} \right] = \left| \begin{array}{cc}-2 &{} \gamma \\ \gamma &{} -2\eta \\ \end{array} \right| =4\eta -\gamma ^2 \end{aligned}$$

Therefore, the profit function for each manufacturer will be concave if $4\eta >\gamma ^2$. Having the information about the two manufacturers’ decisions, the common retailer would use them to maximize her profit. Using $w_1^{RB}$, $w_2^{RB}$, $\theta _1^{RB}$, and $\theta _2^{RB}$, the profit function of the common retailer is obtained as follows:

$$\begin{aligned}\varPi _r^{RB}&=\frac{2\eta {m_1}^{RB}((a-m_1^{RB}+m_2^{RB} \beta ) (4 \eta -\gamma ^2)+(a k-m_2^{RB}+m_1^{RB} \beta ) (2 \beta \eta -\gamma \delta ))}{\varDelta _{rb}}\\&\quad + \frac{2\eta {m_2}^{RB}((a k-m_2^{RB}+m_1^{RB} \beta )(4 \eta -\gamma ^2)+(a-m_1^{RB}+m_2^{RB} \beta ) (2 \beta \eta -\gamma \delta ))}{\varDelta _{rb}} \end{aligned}$$

Therefore, profit margins are obtained by solving $\frac{\partial \varPi _{r}^{RB}}{\partial m_1^{RB}}=0$ and $\frac{\partial \varPi _{r}^{RB}}{\partial m_2^{RB}}=0$, simultaneously. On simplification, $m_1^{RB}=\frac{a(1+ k \beta )}{2(1- \beta ^2)}$ and $m_2^{RB}=\frac{a (k+\beta )}{2(1- \beta ^2)}$ . Note that the value of the determinant of the Hessian matrix for the retailer’s profit function is obtained as:

$$\begin{aligned}&H_r^{RB} = \left| \begin{array}{cc} \frac{\partial ^2\varPi _r^{RB}}{\partial {{m_{1}^{RB}}^2}} &{} \frac{\partial ^2\varPi _r^{RB}}{\partial m_{1}^{RB}\partial m_2^{RB}} \\ \frac{\partial ^2\varPi _r^{RB}}{\partial {{m_{2}^{RB}}}\partial m_1^{RB}} &{} \frac{\partial ^2\varPi _r^{RB}}{\partial {m_{2}^{RB}}^{2}} \\ \end{array} \right| \\&H_r^{RB}= \left| \begin{array}{cc} \frac{-2 \gamma (2 \beta \delta -2 \gamma ) \eta -8X \eta ^2}{\varDelta _{rb}} &{} \frac{8 \beta \eta ^2-2 \gamma (2 \beta \gamma -2 \delta ) \eta }{\varDelta _{rb}} \\ \frac{8 \beta \eta ^2-2 \gamma (2 \beta \gamma -2 \delta ) \eta }{\varDelta _{rb}} &{} \frac{-2 \gamma (2 \beta \delta -2 \gamma ) \eta -8 X \eta ^2}{\varDelta _{rb}} \\ \end{array} \right| =\frac{16 (1-\beta ^2) \eta ^2}{\varDelta _{rb}}>0 \end{aligned}$$

Therefore, the profit function for the retailer in Scenario RB is concave.

C Optimal decision in scenario MC

The optimal solution of the retailer’s optimization problem defined in Eq. (4) is obtained by solving $\frac{\partial \varPi _{r}^{MC}}{\partial p_1^{MC}}=0$ and $\frac{\partial \varPi _{r}^{MC}}{\partial p_2^{MC}}=0$, simultaneously. After simplification, the retailer’s response is obtained as

• $p_1^{MC}=\frac{a+a k \beta +w_1^{MC}(1- \beta ^2)+(\gamma -\beta \delta ) \theta _1^{MC}+(\beta \gamma -\delta ) \theta _2^{MC}}{2(1- \beta ^2)}$

• $p_2^{MC}=\frac{w_2^{MC}(1-\beta ^2)+a (k+\beta )+(\beta \gamma -\delta ) \theta _1^{MC}+\gamma \theta _2^{MC}-\beta \delta \theta _2^{MC}}{2(1- \beta ^2)}$.

The value of the determinant of the Hessian matrix ($H_r^{MC}$) for the retailer’s profit function is obtained as follows:

$$\begin{aligned} H_r^{MC} = \left[ \begin{array}{cc}\frac{\partial ^2 \varPi _{r}^{MC}}{\partial {p_1^{MC}}^2} &{} \frac{\partial ^2\varPi _{r}^{MC}}{\partial p_1^{MC}\partial p_2^{MC}} \\ \frac{\partial ^2\varPi _{r}^{MC}}{\partial p_1^{MC}\partial p_2^{MC}} &{} \frac{\partial ^2\varPi _{r}^{MC}}{\partial {p_2^{MC}}^2} \\ \end{array} \right] = \left| \begin{array}{cc}-2 &{} 2\beta \\ 2\beta &{} -2\\ \end{array} \right| =2(1-\beta ^2)>0 \end{aligned}$$

Therefore, the profit function for the retailer is concave. By substituting optimal responses in Eq. (5), the total profit function for two manufacturers is obtained as

$$\begin{aligned}\varPi _{m}^{MC}&=\frac{a w_1^{MC}-{w_1^{MC}}^2+w_1^{MC} (w_2^{MC} \beta +\gamma \theta _1^{MC}-\delta \theta _2^{MC})-2 \eta {\theta _1^{MC}}^2}{2}\\&\quad +\frac{a k w_2^{MC}-w_2^{MC} (w_2^{MC}-w_1^{MC} \beta +\delta \theta _1^{MC})+w_2^{MC} \gamma \theta _2^{MC}-2 \eta {\theta _2^{MC}}^2}{2} \end{aligned}$$

By solving first-order conditions, $\frac{\partial \varPi _{m}^{MC}}{\partial w_1^{MC}} = 0$;$\frac{\partial \varPi _{m}^{MC}}{\partial \theta _1^{MC}} = 0$; $\frac{\partial \varPi _{m}^{MC}}{\partial w_2^{MC}} = 0$;$\frac{\partial \varPi _{m}^{MC}}{\partial \theta _2^{MC}} = 0$; simultaneously, we obtain responses for manufacturers, which are presented in Table 4. To verify concavity, the Hessian matrix for total profit function($H_m^{MC}$) is computed as follows:

$$\begin{aligned} H_m^{MC}=\left[ \begin{array}{cccc} \frac{\partial ^2\varPi _{m}^{MC}}{\partial {{w_{1}^{MC}}^2}} &{} \frac{\partial ^2\varPi _{m}^{MC}}{\partial w_{1}^{MC}\partial \theta _1^{MC}} &{} \frac{\partial ^2\varPi _{m}^{MC}}{\partial w_{1}^{MC}\partial w_{2}^{MC}} &{} \frac{\partial ^2\varPi _{m}^{MC}}{\partial w_{1}^{MC}\partial \theta _{2}^{MC}}\\ \frac{\partial ^2\varPi _{m}^{MC}}{\partial {{w_{1}^{MC}}}\partial \theta _1^{MC}} &{} \frac{\partial ^2\varPi _{m}^{MC}}{\partial {\theta _{1}^{MC}}^{2}} &{} \frac{\partial ^2\varPi _{m}^{MC}}{\theta _{1}^{MC}\partial w_{2}^{MC}}&{} \frac{\partial ^2\varPi _{m}^{MC}}{\theta _{1}^{MC} \partial \theta _{2}^{MC}}\\ \frac{\partial ^2\varPi _{m}^{MC}}{\partial { w_{1}^{MC}} \partial w_{2}^{MC}} &{} \frac{\partial ^2\varPi _{m}^{MC}}{\partial \theta _1^{MC}\partial w_{2}^{MC}} &{} \frac{\partial ^2\varPi _{m}^{MC}}{\partial {w_{2}^{MC}}^{2}}&{} \frac{\partial ^2\varPi _{m}^{MC}}{\partial w_{2}^{MC}\partial \theta _{2}^{MC}}\\ \frac{\partial ^2\varPi _{m}^{MC}}{\partial { w_{1}^{MC}} \theta _{2}^{MC}} &{} \frac{\partial ^2\varPi _{m}^{MC}}{\partial \theta _1^{MC}\theta _{2}^{MC}} &{} \frac{\partial ^2\varPi _{m}^{MC}}{\partial {w_{2}^{MC}} \partial \theta _{2}^{MC}}&{} \frac{\partial ^2\varPi _{m}^{MC}}{\partial {\theta _{2}^{MC}}^{2}}\\ \end{array} \right] = \left[ \begin{array}{ccccc}-1 &{} \frac{\gamma }{2} &{} \beta &{} \frac{-\delta }{2}\\ \frac{\gamma }{2} &{} -2\eta &{} \frac{-\delta }{2}&{} 0\\ \beta &{} \frac{-\delta }{2} &{}-1&{} \frac{\gamma }{2}\\ \frac{-\delta }{2}&{} 0&{} \frac{\gamma }{2}&{} -2\eta \\ \end{array} \right] \end{aligned}$$

The values of leading principal minors for the matrix ($H_m^{MC}$) are obtained as $|H_{m1}^{MC}|=-1$; $|H_{m2}^{MC}|=\frac{8\eta -\gamma ^2}{4}>0$;$|H_{m3}^{MC}|=\frac{-(8 (1 - \beta ^2) \eta -\gamma ^2 + 2 \beta \gamma \delta - \delta ^2 )}{4}<0$; and $|H_{m4}^{MC}|=\frac{\varDelta _{mc}}{16}$, respectively. Therefore, the combined profit function for two manufacturers is also concave if $\varDelta _{mc}>0$.

D Optimal decision in scenario RC

Similar to Scenario RB, we assume $m_i^{RC}=p_i^{RC}-w_i^{RC}$ represents profit margin for product i and substitute in Eqs. (4) and (5). Therefore, wholesale prices and green-degrees are obtained by solving $\frac{\partial \varPi _{m}^{RC}}{\partial w_1^{RC}}=0$; $\frac{\partial \varPi _{m}^{RC}}{\partial \theta _1^{RC}}=0$; $\frac{\partial \varPi _{m}^{RC}}{\partial w_2^{RC}}=0$, and $\frac{\partial \varPi _{m}^{RC}}{\partial \theta _2^{RC}}=0$ simultaneously. After simplification, wholesale price and GLs are obtained as follows:

• $w_1^{RC}=\frac{2\eta }{\varDelta _{rc}}\left[ 2 (2 (a+a k \beta -m_1^{RC} (1-\beta ^2)) \eta -(a k-m_2^{RC}+m_1^{RC} \beta ) \gamma \delta )\right.$

• $\left. - (a-m_1^{RC}+m_2^{RC} \beta ) (\gamma ^2+\delta ^2)\right]$

• $w_2^{RC}=\frac{2\eta }{\varDelta _{rc}}\left[ 4(a (k+\beta )-m_2^{RC} (1-\beta ^2))+2(a-m_1^{RC}+m_2^{RC} \beta ) \gamma \delta \right.$

• $\left. - (a k-m_2^{RC}+m_1^{RC} \beta ) (\gamma ^2+\delta ^2) \right]$

• $\theta _1^{RC}=\frac{1}{\varDelta _{rc}}\left[ 4 (a (1+k \beta ) \gamma -a (k+\beta ) \delta -(1-\beta ^2) (m_1^{RC} \gamma -m_2^{RC} \delta )) \eta \right.$

• $\left. -(\gamma ^2-\delta ^2) (m_2^{RC} \beta \gamma -m_1^{RC} \gamma \right.$

• $\left. -m_2^{RC} \delta +m_1^{RC} \beta \delta +a (\gamma +k \delta ))\right]$

• $\theta _2^{RC}=\frac{1}{\varDelta _{rc}}\left[ 4 (a (k+\beta ) \gamma -a (1+k \beta ) \delta -(1-\beta ^2) (m_2^{RC} \gamma -m_1^{RC} \delta )) \eta \right.$

• $\left. -(\gamma ^2-\delta ^2) ((a k-m_2^{RC}+m_1^{RC} \beta ) \gamma +(a-m_1^{RC}+m_2^{RC} \beta ) \delta )\right]$

To verify concavity, the Hessian matrix for combined profit function ($H_m^{RC}$) is computed as follows:

$$\begin{aligned} H_m^{RC} = \left[ \begin{array}{cccc} \frac{\partial ^2\varPi _{m}^{RC}}{\partial {{w_{1}^{RC}}^2}} &{} \frac{\partial ^2\varPi _{m}^{RC}}{\partial w_{1}^{RC}\partial \theta _1^{RC}} &{} \frac{\partial ^2\varPi _{m}^{RC}}{\partial w_{1}^{RC}\partial w_{2}^{RC}} &{} \frac{\partial ^2\varPi _{m}^{RC}}{\partial w_{1}^{RC}\partial \theta _{2}^{RC}}\\ \frac{\partial ^2\varPi _{m}^{RC}}{\partial {{w_{1}^{RC}}}\partial \theta _1^{RC}} &{} \frac{\partial ^2\varPi _{m}^{RC}}{\partial {\theta _{1}^{RC}}^{2}} &{} \frac{\partial ^2\varPi _{m}^{RC}}{\theta _{1}^{RC}\partial w_{2}^{RC}}&{} \frac{\partial ^2\varPi _{m}^{RC}}{\theta _{1}^{RC} \partial \theta _{2}^{RC}}\\ \frac{\partial ^2\varPi _{m}^{RC}}{\partial { w_{1}^{RC}} \partial w_{2}^{RC}} &{} \frac{\partial ^2\varPi _{m}^{RC}}{\partial \theta _1^{RC}\partial w_{2}^{RC}} &{} \frac{\partial ^2\varPi _{m}^{RC}}{\partial {w_{2}^{RC}}^{2}}&{} \frac{\partial ^2\varPi _{m}^{RC}}{\partial w_{2}^{RC}\partial \theta _{2}^{RC}}\\ \frac{\partial ^2\varPi _{m}^{RC}}{\partial { w_{1}^{RC}} \theta _{2}^{RC}} &{} \frac{\partial ^2\varPi _{m}^{RC}}{\partial \theta _1^{RC}\theta _{2}^{RC}} &{} \frac{\partial ^2\varPi _{m}^{RC}}{\partial {w_{2}^{RC}} \partial \theta _{2}^{RC}}&{} \frac{\partial ^2\varPi _{m}^{RC}}{\partial {\theta _{2}^{RC}}^{2}}\\ \end{array} \right] = \left[ \begin{array}{ccccc}-2 &{} \gamma &{} 2\beta &{} -\delta \\ \gamma &{} -2\eta &{} -\delta &{} 0\\ 2\beta &{} -\delta &{}-2&{} \gamma \\ -\delta &{} 0&{} \gamma &{} -2\eta \\ \end{array} \right] \end{aligned}$$

Therefore, the values of leading principal minors for the Hessian matrix for combined profit function ($H_r^{RC}$) are obtained as $|H_{m1}^{RC}|=-2<0$, $|H_{m2}^{RC}|=(4\eta -\gamma ^2)>0$, $|H_{m3}^{RC}|=-2(8 (1 - \beta ^2) \eta -\gamma ^2 + 2 \beta \gamma \delta - \delta ^2)<0$, and $|H_{m4}^{RC}|=\varDelta _{rc}$, respectively. Therefore, the total profit function for both manufacturers is also concave if $\varDelta _{rc}>0$. By substituting the optimal response for two manufacturers, the profit function for the retailer is obtained as follows:

• $\varPi _{r}^{RC}=\frac{2\eta }{\varDelta _{rc}}\left[ 4 m_1^{RC} m_2^{RC} (\gamma \delta +\beta ^2 \gamma \delta -\beta (\gamma ^2+\delta ^2-2 \eta )-2 \beta ^3\eta )\right.$

• $\left. +({m_1^{RC}}^2+{m_2^{RC}}^2) ((1+\beta ^2) \gamma ^2-4 \beta \gamma \delta +(1+\beta ^2) \delta ^2-4 (1-\beta ^2) \eta )+\right.$

• $\left. -a (m_1^{RC} ((1-k \beta ) \gamma ^2+2 (k-\beta ) \gamma \delta +(1-k \beta ) \delta ^2-4 (1-\beta ^2) \eta )\right.$

• $\left. +{m_2}^{RC} (\beta (\gamma ^2+\delta ^2)-2 \gamma \delta -k (\gamma ^2-2 \beta \gamma \delta +\delta ^2-4 (1-\beta ^2) \eta )))\right]$

Therefore, the profit margins for each products for the retailer can be obtained by solving $\frac{\partial \varPi _{r}^{RC}}{\partial m_1^{RC}} = 0$ and $\frac{\partial \varPi _{r}^{RC}}{\partial m_2^{RC}} = 0$, and the corresponding solution is $m_1^{RC}=\frac{a+a k \beta }{2-2 \beta ^2}$ and $m_2^{RC}=\frac{a (k+\beta )}{2 (1-\beta ^2)}$. The profit function for the retailer is also concave because the value of the determinant of the Hessian matrix for the retailer profit function ($H_r^{RC}$) is

$$\begin{aligned} H_r^{RC}= & {} \left| \begin{array}{cccc} \frac{\partial ^2\varPi _{r}^{RC}}{\partial {{m_{1}^{RC}}^2}} &{} \frac{\partial ^2\varPi _{r}^{RC}}{\partial m_{1}^{RC}\partial m_2^{RC}} \\ \frac{\partial ^2\varPi _{r}^{RC}}{\partial m_{1}^{RC}\partial m_2^{RC}} &{} \frac{\partial ^2\varPi _{r}^{RC}}{\partial {{m_{2}^{RC}}^2}} \end{array} \right| \\= & {} \left| \begin{array}{ccccc} \frac{4 [-\beta \gamma \delta - (1-\beta ^2) \eta + \eta (1+\beta ^2) (\gamma ^2+ \delta ^2)]}{\varDelta _{rc}} &{} \frac{8 \eta (\gamma \delta +\beta ^2 \gamma \delta -\beta (\gamma ^2+\delta ^2-2 \eta )-2 \beta ^3 \eta )}{\varDelta _{rc}} \\ \frac{8 \eta (\gamma \delta +\beta ^2 \gamma \delta -\beta (\gamma ^2+\delta ^2-2 \eta )-2 \beta ^3 \eta )}{\varDelta _{rc}} &{} \frac{4 [- \beta \gamma \delta - (1-\beta ^2) \eta +\eta (1+\beta ^2) (\gamma ^2+ \delta ^2)]}{\varDelta _{rc}} \\ \end{array} \right| \\= & {} \frac{16 (1-\beta ^2)^2 \eta ^2}{\varDelta _{rc}}>0 \end{aligned}$$

Therefore, the profit function for the retailer is also concave. By using back substitution, one can find the optimal decision as presented in Table 4.

Note that the optimal decision in Scenario VN is similar to that in Scenario RC, however, one needs to solve $\frac{\partial \varPi _{m}^{VN}}{\partial w_1^{VN}}=0$; $\frac{\partial \varPi _{m}^{VN}}{\partial \theta _1^{VN}}=0$; $\frac{\partial \varPi _{m}^{VN}}{\partial w_2^{VN}}=0$, and $\frac{\partial \varPi _{m}^{VN}}{\partial \theta _2^{VN}}=0$; $\frac{\partial \varPi _{r}^{VN}}{\partial m_1^{VN}} = 0$ and $\frac{\partial \varPi _{r}^{VN}}{\partial m_2^{VN}} = 0$, simultaneously. Note that the profit margins for per unit products for the retailer in Scenario VN are $m_1^{VN}=\frac{2 a \eta (2 (3+4 k \beta +\beta ^2) \eta -\gamma (\gamma +k \beta \gamma +(k+\beta ) \delta ))}{(1-\beta ^2) \varDelta _{vn}}$ and $m_1^{VN}=\frac{2 a \eta (2 (4 \beta +k (3+\beta ^2)) \eta -\gamma ((k+\beta ) \gamma +\delta +k \beta \delta ))}{(1-\beta ^2) \varDelta _{vn}}$, respectively. The corresponding optimal outcome is presented in Proposition 5.

E Proof of Propositions 1 and 2

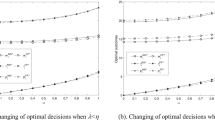
See Tables 6 and 7 and Fig. 7.

We represent the difference between manufacturers’ and the retailer’s profits and GLs in Table 6.

Table 6 Profit and GL differences in five game structures when $\beta =0$, $\delta =0$, and $k=1$

After, simplification we obtain the relation. Similarly, we present the difference between manufacturers’ and retailer’s profit, in Table 7.

Table 7 Profit differences for the manufacturers and retailer in five scenarios when $\delta =0$; $\gamma =0$; and $k=1$

F Optimal decision under TRS contract

The optimal decision for the retailer optimization problem in Eq. (7) is obtained by solving the following first-order conditions, $\frac{\partial \varPi _{r}^{TRS}}{\partial p_{1}^{TRS}} =0$ and $\frac{\partial \varPi _{r}^{TRS}}{\partial p_{2}^{TRS}}=0$, respectively. On simplification, the retailer’s response to the market prices is obtained as follows:

• $p_1^{TRS}=\frac{1}{4 \rho _1 \rho _2-\beta ^2 (\rho _1+\rho _2)^2}[2 (w_1^{TRS}-w_2^{TRS} \beta +(a+\gamma \theta _1^{TRS}-\delta \theta _2^{TRS}) \rho _1) \rho _2+\beta (\rho _1^{TRS}+\rho _2^{TRS}) (w_2^{TRS}-w_1^{TRS} \beta +(a k-\delta \theta _1^{TRS}+\gamma \theta _2^{TRS}) \rho _2)]$

• $p_2^{TRS}=\frac{1}{4 \rho _1 \rho _2-\beta ^2 (\rho _1+\rho _2)^2}[w_2^{TRS} (2-\beta ^2) \rho _1+w_1^{TRS} \beta (\rho _1-\rho _2)+w_2^{TRS} \beta ^2 \rho _1-\rho _1 (2 a k \rho _2-2 \delta \theta _1^{TRS} \rho _1+2 \gamma \theta _2^{TRS} \rho _1)+(\rho _1+\rho _2)(a \beta +\beta (\gamma \theta _1^{TRS}-\delta \theta _2^{TRS}) )]$

Based on the retailer’s response, if two upstream manufacturers want to employ the centralized decision, then the optimal supply chain profits would be achieved if $p_1^{TRS}=p_1^{c}$ and $p_2^{TRS}=p_2^{c}$, respectively. On simplification, the GLs of two products are obtained as follows:

• $\theta _1^{TRS}=\frac{1}{(\gamma ^2-\delta ^2) \varDelta _c \rho _1 \rho _2}[w_1^{TRS} (\gamma ^4+\delta ^4+16 \beta \gamma \delta \eta -8 \delta ^2 \eta +16 (1-\beta ^2) \eta ^2-2 \gamma ^2 (\delta ^2+4 \eta )) (\beta \delta \rho _1-\gamma \rho _2)+w_2^{TRS} (\gamma ^4+\delta ^4+16 \beta \gamma \delta \eta -8 \delta ^2 \eta +16 (1-\beta ^2) \eta ^2-2 \gamma ^2 (\delta ^2+4 \eta )) (\beta \gamma \rho _2-\delta \rho _1)+a ((\gamma ^3+k \gamma ^2 \delta -k \delta (\delta ^2-4 \eta )-\gamma (\delta ^2+4 \eta )-(\gamma ^2-\delta ^2)) \rho _1 \rho _2-8 \beta ^2 \eta ^2 (\rho _1-\rho _2) (k \delta \rho _2-\gamma \rho _2)+2 \beta \eta (4 k \gamma \eta (\rho _1-\rho _2) \rho _2+4 \delta \eta \rho _1 (\rho _2-\rho _1)+\delta ^3 \rho _1 (\rho _1+\rho _2)+k \gamma ^3 \rho _2 (\rho _1+\rho _2)+k \gamma \delta ^2 (2 \rho _1^2-5 \rho _1 \rho _2+\rho _2^2)+\gamma ^2 \delta (\rho _1^2-5 \rho _1 \rho _2+2 \rho _2^2)))]$

• $\theta _2^{TRS}=\frac{1}{(\gamma ^2-\delta ^2) \varDelta _c \rho _1 \rho _2}[(w_1^{TRS} (\gamma ^4+\delta ^4+16 \beta \gamma \delta \eta -8 \delta ^2 \eta +16 (1-\beta ^2) \eta ^2-2 \gamma ^2 (\delta ^2+4 \eta )) (\beta \gamma \rho _1-\delta \rho _1)-w_2^{TRS} (\gamma ^4+\delta ^4+16 \beta \gamma \delta \eta -8 \delta ^2 \eta +16 (1-\beta ^2) \eta ^2-2 \gamma ^2 (\delta ^2+4 \eta )) (\gamma \rho _1-\beta \delta \rho _2)+a ((\delta ^2-\gamma ^2) (k \gamma (\gamma ^2-\delta ^2-4 \eta )+\delta (\gamma ^2-\delta ^2+4 \eta )) \rho _1 \rho _2-8 \beta ^2 \eta ^2 (\rho _1-\rho _2) (k \gamma \rho _1-\delta \rho _2)+2 \beta \eta (4 k \delta \eta (\rho _1-\rho _2) \rho _2+4 \gamma \eta \rho _1 (\rho _2-\rho _1)+\gamma ^3 \rho _1 (\rho _1+\rho _2)+k \delta ^3 \rho _2 \delta ^2 (\rho _1^2-5 \rho _1 \rho _2+2 \rho _2^2)))]$.

Finally, optimal GSC profits will be achieved if $\theta _1^{TRS}=\theta _1^{c}$ and $\theta _2^{TRS}=\theta _2^{c}$, respectively. On simplification, wholesale prices are obtained as follows:

• $w_1^{TRS}=\frac{2 a \beta \eta (4 (1-\beta ^2) \eta -2 \gamma \delta -\beta (\gamma ^2+\delta ^2)+k (\gamma ^2-2 \beta \gamma \delta +\delta ^2)) (\rho _1-\rho _2)}{(1-\beta ^2) \varDelta _c}$

• $w_2^{TRS}=\frac{2 a \beta \eta (4 (1-\beta ^2) \eta -(1-k \beta ) \gamma ^2+2 (k-\beta ) \gamma \delta +(1-k \beta ) \delta ^2) (\rho _1-\rho _2)}{(1-\beta ^2)\varDelta _c^2}$.

Finally, by using back substitution, one can obtain the profits as presented in Proposition  6. As expected, if $k=1$ the difference between GLs in the centralized decision and in Scenarios MB or MC are $\theta _1^{C}-\theta _1^{MC}=\theta _2^{C}-\theta _2^{MC}=\frac{4 a (1-\beta ) (\gamma -\delta ) \eta }{(\gamma -\delta )^4-12 (1-\beta ) (\gamma -\delta )^2 \eta +32 (1-\beta )^2 \eta ^2}>0$ and $\theta _1^{C}-\theta _1^{MB}=\theta _2^{C}-\theta _2^{MB}=\frac{4 a (\gamma +(-2+\beta ) \delta ) \eta }{\varDelta _{1c}\varDelta _{1mb}}>0$, respectively. Therefore, if the GSC members adopt centralized GLs, consumers always receive products with higher GLs.

G Sensitivity analysis

A graphical representation of the sensitivity analysis is presented in the figure below:

Fig. 7

Sensitivity analysis for the parameters $\beta$, $\delta$, $\eta$, and $\gamma$