Information dynamics based self-adaptive reservoir for delay temporal memory tasks

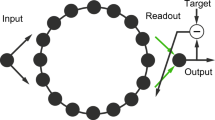
Abstract

Recurrent neural networks of the reservoir computing (RC) type have been found useful in various time-series processing tasks with inherent non-linearity and requirements of variable temporal memory. Specifically for delayed response tasks involving the transient memorization of information (temporal memory), self-adaptation in RC is crucial for generalization to varying delays. In this work using information theory, we combine a generalized intrinsic plasticity rule with a local information dynamics based schema of reservoir neuron leak adaptation. This allows the RC network to be optimized in a self-adaptive manner with minimal parameter tuning. Local active information storage, measured as the degree of influence of previous activity on the next time step activity of a neuron, is used to modify its leak-rate. This results in RC network with non-uniform leak rate which depends on the time scales of the incoming input. Intrinsic plasticity (IP) is aimed at maximizing the mutual information between each neuron’s input and output while maintaining a mean level of activity (homeostasis). Experimental results on two standard benchmark tasks confirm the extended performance of this system as compared to the static RC (fixed leak and no IP) and RC with only IP. In addition, using both a simulated wheeled robot and a more complex physical hexapod robot, we demonstrate the ability of the system to achieve long temporal memory for solving a basic T-shaped maze navigation task with varying delay time scale.

Appendix

The activation of each reservoir neuron with a $\tt{tanh}$ non-linearity with slope(a) and shape(b) parameters can be represented as $\theta = \tt{tanh}(ax+b).$ The activations are time dependent as shown in Eq. (4), however here we neglect the time variable for mathematical convenience. The tanh non-linearity can be represented in an exponential form as follows:

$$\theta = \mathtt{tanh}(ax+b) = \frac{e^{2(ax+b)}-1}{e^{2(ax+b)}+1} $$

(17)

Differentiating this w.r.t x, a and b and representing in terms of θ we get the following set of base equations:

$$\begin{aligned} &\frac{\partial{\theta}}{\partial{x}} = a(1-\theta^2), \\ &\frac{\partial{\theta}}{\partial{a}} = x(1-\theta^2), \\ &\frac{\partial{\theta}}{\partial{b}} =(1-\theta^2) \end{aligned} $$

(18)

The probability distribution of the two-parameter Weibull random variable θ is given as follows:

$$f_{weib}(\theta;\beta,\alpha) = \left\{\begin{array}{ll} \frac{\alpha}{\beta} \left(\frac{\theta}{\beta} \right)^{\alpha-1}exp- \left(\frac{\theta}{\beta} \right)^{\alpha} &\hbox{if } \theta \geq 0 \\ 0 &\hbox{if } \theta < 0 \\ \end{array} \right. $$

(19)

Inorder to find a stochastic rule for the calculation of the neuron transfer functin parameters a and b, we need to minimize the Kullback–Leibler (KL) divergence between the real output distribution f _θ and the desired distribution f _weib . The KL-divergence (D _KL (f _θ , f _weib )) is given by:

$$\begin{aligned} D = D_{KL}(f_\theta,f_{weib}) =& \int f_\theta(\theta)log\Big(\frac{f_\theta(\theta)}{f_{weib}(\theta)}\Big)\mathrm{d}\theta \\ =& \int f_\theta(\theta)log f_\theta(\theta)\mathrm{d}\theta -(\alpha-1)\int f_\theta(\theta)log(\theta)\mathrm{d}\theta\\& + \frac{1}{\beta^\alpha}\int f_\theta(\theta)\theta^\alpha \mathrm{d}\theta + C \end{aligned} $$

(20)

Using the relation $f_\theta(\theta) = \frac{f_x(x)}{\frac{\partial\theta}{\partial x}}$ for a single neuron with input x and output θ and representing the integrals in terms of the expectation(E) quantities, the above relation can be simplified to (here C is a constant):

$$\begin{aligned} D =& -E\left[log\left(\frac{\partial{\theta}}{\partial{x}}\right)\right] +E[log f_x(x)] +\frac{1}{\beta^\alpha}E(\theta^\alpha)\\ & -(\alpha-1)E(log(\theta))+C \end{aligned} $$

(21)

Using the partial derivatives from Eq. (18) and differentiating D w.r.t the parameter b yields:

$$\begin{aligned} \frac{\partial{D}}{\partial{b}}&=E\left[2\theta + \frac{\alpha}{\beta^\alpha}\theta^{\alpha-1}(1-\theta^2)-(\alpha-1)\theta^{-1}(1-\theta^2)\right] \\ &=E\left[2\theta + \theta^{-1}(1-\theta^2)\left(\frac{\alpha}{\beta^\alpha}\theta^\alpha-\alpha+1\right)\right] \end{aligned} $$

(22)

Similarly differentiating D w.r.t the parameter a results in:

$$\frac{\partial{D}}{\partial{a}} = E\left[2\theta x + x\theta^{-1}(1-\theta^2) \left(\frac{\alpha}{\beta^\alpha}\theta^\alpha - \alpha + 1\right) - \frac{1}{a} \right] $$

(23)

From the above equations we get the following on-line learning rule with stochastic gradient descent with learning rate η

$$\Updelta b = -\eta\Big[2\theta + \theta^{-1}(1-\theta^2)\Big(\frac{\alpha}{\beta^\alpha}\theta^\alpha-\alpha+1\Big)\Big]. $$

(24)

$$\Updelta a = \frac{\eta}{a}+ x\Updelta b $$

(25)

Note: This relationship between the neuron parameter update rules ($\Updelta a$ and $\Updelta b$) is generic and valid irrespective of the neuron non-linearity or target probability distribution.