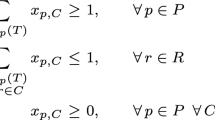Abstract
We consider the (block-angular) min–max resource sharing problem, which is defined as follows. Given finite sets \({\mathcal{R}}\) of resources and \({\mathcal{C}}\) of customers, a convex set \({\mathcal{B}_c}\), called block, and a convex function \({g_c:\mathcal{B}_c\to\mathbb{R}_{+}^{\mathcal{R}}}\) for every \({c\in\mathcal{C}}\), the task is to find \({b_c\in\mathcal{B}_c\ (c\in\mathcal{C})}\) approximately attaining \({\lambda^*:=\inf\{\max_{r\in\mathcal{R}}\sum_{c\in\mathcal{C}}(g_c(b_c))_r \mid b_c\in\mathcal{B}_c\ (c\in\mathcal{C})\}}\). As usual we assume that g c can be computed efficiently and we have a constant σ ≥ 1 and oracle functions \({f_c : \mathbb{R}_{+}^{\mathcal{R}} \rightarrow \mathcal{B}_c}\), called block solvers, which for \({c \in \mathcal{C}}\) and \({y \in \mathbb{R}_{+}^{\mathcal{R}}}\) return an element \({b_c \in \mathcal{B}_c}\) with \({y^{\scriptscriptstyle\top}{g_c(b_c)} \leq \sigma \inf_{b \in \mathcal{B}_c} y^{\scriptscriptstyle\top}{g_c(b)}}\). We describe a simple algorithm which solves this problem with an approximation guarantee σ(1 + ω) for any ω > 0, and whose running time is \({O(\theta(|\mathcal{C}|+|\mathcal{R}|) \log|\mathcal{R}|(\log\log|\mathcal{R}|+\omega^{-2}))}\) for any fixed σ ≥ 1, where θ is the time for an oracle call. This generalizes and improves various previous results. We also prove other bounds and describe several speed-up techniques. In particular, we show how to parallelize the algorithm efficiently. In addition we review another algorithm, variants of which were studied before. We show that this algorithm is almost as fast in theory, but it was not competitive in our experiments. Our work was motivated mainly by global routing in chip design. Here the blocks are mixed-integer sets (whose elements are associated with Steiner trees), and we combine our algorithm with randomized rounding. We present experimental results on instances resulting from recent industrial chips, with millions of customers and resources. Our algorithm solves these instances nearly optimally in less than two hours.
Similar content being viewed by others
References
Albrecht C.: Global routing by new approximation algorithms for multicommodity flow. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 20, 622–632 (2001)
Bienstock D.: Potential function methods for approximately solving linear programming problems: theory and practice. Kluwer Academic Publishers, Norwell (2002)
Bienstock D., Iyengar G.: Approximating fractional packings and coverings in \({O(\frac{1}{\epsilon})}\) iterations. SIAM J. Comput. 35, 825–854 (2006)
Carden R.C. IV, Li J., Cheng C.-K.: A global router with a theoretical bound on the optimum solution. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 15, 208–216 (1996)
Charikar, M., Chekuri, C., Goel, A., Guha, S., and Plotkin, S.: Approximating a finite metric by a small number of tree metrics. In: Proceedings of the 39th Annual IEEE Symposium on Foundations of Computer Science, 379–388 (1998)
Fleischer L.K.: Approximating fractional multicommodity flow independent of the number of commodities. SIAM J. Discret. Math. 13, 505–520 (2000)
Garg N., Könemann J.: Faster and simpler algorithms for multicommodity flow and other fractional packing problems. SIAM J. Comput. 37, 630–652 (2007)
Grigoriadis M.D., Khachiyan L.D.: Fast approximation schemes for convex programs with many blocks and coupling constraints. SIAM J. Optim. 4, 86–107 (1994)
Grigoriadis M.D., Khachiyan L.D.: Coordination complexity of parallel price-directive decomposition. Math. Oper. Res. 21, 321–340 (1996)
Hennessy J.L., Patterson D.A.: Computer Architecture: A Quantitative Approach, 4th edn. Morgan Kaufmann, San Francisco (2007)
IEEE Standard for Binary Floating-Point Arithmetic. ANSI/IEEE Std 754–2008, IEEE (2008)
Intel®64 and IA-32 Architectures Software Developer’s Manual, vol. 3A, rev. 037, order number 253668-037US, January 2011. http://www.intel.com
Jansen K., Zhang H.: Approximation algorithms for general packing problems and their application to the multicast congestion problem. Math. Program. A 114, 183–206 (2008)
Khandekar, R.: Lagrangian relaxation based algorithms for convex programming problems. PhD thesis, Indian Institute of Technology, Delhi (2004)
Müller, D.: Optimizing yield in global routing. In: Proceedings of the IEEE International Conference on Computer-Aided Design, 480–486 (2006)
Owens, S., Sarkar, S., Sewell, P.: A Better x86 Memory Model: x86-TSO. In: Proceedings of the 22nd International Conference on Theorem Proving in Higher Order Logics; LNCS 5674, pp. 391–407. Springer, Berlin (2009)
Plotkin S.A., Shmoys D.B., Tardos É.: Fast approximation algorithms for fractional packing and covering problems. Math. Oper. Res. 2, 257–301 (1995)
Raghavan P.: Probabilistic construction of deterministic algorithms: approximating packing integer programs. J. Comput. Syst. Sci. 37, 130–143 (1988)
Raghavan P., Thompson C.D.: Randomized rounding: a technique for provably good algorithms and algorithmic proofs. Combinatorica 7, 365–374 (1987)
Shahrokhi F., Matula D.W.: The maximum concurrent flow problem. J. ACM 37, 318–334 (1990)
Villavicencio J., Grigoriadis M.D.: Approximate structured optimization by cyclic block-coordinate descent. In: Fischer, H., Riedmüller, B., Schäffler, S. (eds) Applied Mathematics and Parallel Computing, pp. 359–371. Physica-Verlag, Heidelberg (1996)
Vygen J.: Near-optimum global routing with coupling, delay bounds, and power consumption. In: Nemhauser, G., Bienstock, D. (eds) Integer Programming and Combinatorial Optimization; Proceedings of the 10th International IPCO Conference; LNCS 3064, pp. 308–324. Springer, Berlin (2004)
Young, N.E.: Randomized rounding without solving the linear program. In: Proceedings of the 6th ACM-SIAM Symposium on Discrete Algorithms, pp. 170–178 (1995)
Young, N.E.: Sequential and parallel algorithms for mixed packing and covering. In: Proceedings of the 42nd Annual IEEE Symposium on Foundations of Computer Science, pp. 538–546 (2001)
Author information
Authors and Affiliations
Corresponding author
Additional information
Research was done while K. Radke was at the University of Bonn.
Rights and permissions
About this article
Cite this article
Müller, D., Radke, K. & Vygen, J. Faster min–max resource sharing in theory and practice. Math. Prog. Comp. 3, 1–35 (2011). https://doi.org/10.1007/s12532-011-0023-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12532-011-0023-y
Keywords
- Min–max resource sharing
- Fractional packing
- Fully polynomial approximation scheme
- Parallelization
- Global routing
- Chip design