An exact cooperative method for the uncapacitated facility location problem

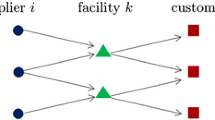
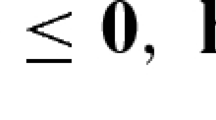Abstract

In this paper, we present a cooperative primal-dual method to solve the uncapacitated facility location problem exactly. It consists of a primal process, which performs a variation of a known and effective tabu search procedure, and a dual process, which performs a lagrangian branch-and-bound search. Both processes cooperate by exchanging information which helps them find the optimal solution. Further contributions include new techniques for improving the evaluation of the branch-and-bound nodes: decision-variable bound tightening rules applied at each node, and a subgradient caching strategy to improve the bundle method applied at each node.

Appendices

Appendix A: Cache implementation details

An efficient implementation of $\mathcal {C}$ is crucial to its performance. In our implementation, $\mathcal {C}$ is a FIFO queue whose maximal size is a predefined parameter. Consequently, an insertion of a new element into a full $\mathcal {C}$ is preceded by the removal of its oldest element. When inserting a new element into $\mathcal {C}$, our implementation does not examine the contents of $\mathcal {C}$ to detect if it is already present, but instead it tests its presence using a counting Bloom filter. A Bloom filter is a data structure originally proposed by Bloom [6] which allows testing efficiently whether a set contains an element (with occasional false positives, but no false negatives). A counting Bloom filter is a variant defined using any vector $\varvec{\mathbf {\beta }}$ of positive integers and a set $H$ of different hash functions $h \in H$ which each map any element possibly in $\mathcal {C}$ to an index of $\varvec{\mathbf {\beta }}$:

• if an element $e$ is added into $\mathcal {C}$, then increment $\varvec{\mathbf {\beta }}_{h(e)}$ by 1 for all $h \in H$,

• therefore an element $e$ is certainly not in $\mathcal {C}$ if there exists $h \in H$ for which $\varvec{\mathbf {\beta }}_{h(e)} = 0$,

• if an element $e$ is removed from $\mathcal {C}$, then decrement $\varvec{\mathbf {\beta }}_{h(e)}$ by 1 for all $h \in H$.

Bloom filters are efficient in time and in space even for very large sets. By hard-coding the maximum size of $\mathcal {C}$ to $2^{16}-1$ elements, we implemented $\varvec{\mathbf {\beta }}$ as an array of 16-bit unsigned integers. In our implementation, the dimension of this array is in the low hundred thousands, and $|H| = 7$. As a consequence, the probability of false positives when testing whether $e \in \mathcal {C}$ is less than 1%.

When trying to insert a new element $e$ into $\mathcal {C}$, the following steps are performed:

• 1. If $\varvec{\mathbf {\beta }}_{h(e)} > 0$ for all $h \in H$, then $e$ is probably already in $\mathcal {C}$: go to step 4.

• 2. If $\mathcal {C}$ is full, then remove the oldest element $e'$ in $\mathcal {C}$ and decrement $\varvec{\mathbf {\beta }}_{h(e')}$ by 1 for all $h \in H$.

• 3. Insert $e$ into $\mathcal {C}$ and increment $\varvec{\mathbf {\beta }}_{h(e)}$ by 1 for all $h \in H$.

• 4. Done.

The counting Bloom filter thus ensures the unicity of the elements in $\mathcal {C}$.

Appendix B: Bundle method iteration limits

Recall that the elements stored in $\mathcal {C}$ are key-value pairs specifying first-order outer approximations of lagrangian dual functions, and the purpose of $\mathcal {C}$ is to provide valid approximations to populate the bundle. Recall also that in our method we apply a bundle method during the evaluation of each node $(\varvec{\mathbf {p}}{},\underline{n}{},\overline{n}{},{\bar{\varvec{\mathbf {\mu }}}})$ selected in $\mathcal {Q}$ by the Branch-and-bound procedure, and that the initial trial point $\varvec{\mathbf {\mu }}^{(0)}$ is set to $\bar{\varvec{\mathbf {\mu }}}$, i.e. the best vector of multipliers found for the parent node. Once our implementation has identified a subset $S$ of valid $(\varvec{\mathbf {\sigma }}, \epsilon )$ pairs present in $\mathcal {C}$, it does not immediately update the bundle with all pairs in $S$. We have found it more convenient to update the bundle using at most $b$ pairs in $S$, with $b$ being the maximum bundle size minus 1. This seemingly arbitrary choice was partly due to certain limitations of [B]TT (the bundle method implementation which we use), however it seems to be effective. In the case where the valid subset size exceeds this number, we update the bundle with the $b$ pairs in $S$ selected as follows: let $\varvec{\mathbf {\mu }}^{(0)}$ be the initial trial point of the bundle method, we select $(\varvec{\mathbf {\sigma }}, \epsilon ) \in S$ minimizing the value $\sum _{j=1}^m\varvec{\mathbf {\mu }}^{(0)} \varvec{\mathbf {\sigma }}_j + \epsilon$. In this manner, we select the most accurate first-order outer approximations, the value $\sum _{j=1}^m\varvec{\mathbf {\mu }}^{(0)} \varvec{\mathbf {\sigma }}_j + \epsilon - \phi (\varvec{\mathbf {p}}{},\underline{n}{},\overline{n}{},{\varvec{\mathbf {\mu }}^{(0)}})$ being the error at $\varvec{\mathbf {\mu }}^{(0)}$ of the approximation defined by $(\varvec{\mathbf {\sigma }}, \epsilon )$.

Recall that in our implementation, a hard limit on the number of iterations to be performed by an application of the bundle method is set. This is either iter_limit_initial for the very first application (at the beginning of which the cache is empty), or iter_limit_other for the others. In all applications other than the first, we use iter_limit_other - $\min \{b, |S|\}$ as the actual iteration limit. In this manner, and provided that iter_limit_other >$b$, the intensity of the search for the optimal multiplier is inversely proportional to the size of the initial bundle, and hence indirectly to the quality of the model of the lagrangian dual.

Appendix C: Fast floating point arithmetic

A large part of the computational effort is expended in the following computations within the bundle method:

• computing reduced costs $\bar{\varvec{\mathbf {c}}}^{\varvec{\mathbf {\mu }}}$,

• generating a subgradient $\varvec{\mathbf {\sigma }}^{(t)}$,

• computing $\sum _{j=1}^m\varvec{\mathbf {\mu }}_j^{(0)} \varvec{\mathbf {\sigma }}_j + \epsilon$.

While the theoretical complexity of these operations cannot be reduced, in practice we can speed these up by performing as many of them as possible in the SSE registers which are now standard on x86 processors. Consider the computation of the reduced costs given $\varvec{\mathbf {\mu }}\in \mathbb {R}^m$:

$$\begin{aligned} \forall i \in \{1,\ldots ,n\},\quad \bar{\varvec{\mathbf {c}}}^{\varvec{\mathbf {\mu }}}_i \leftarrow \,\varvec{\mathbf {c}}_i + \sum _{j=1}^m\min \left\{ 0, \varvec{\mathbf {s}}_{ij} - \varvec{\mathbf {\mu }}_j\right\} . \end{aligned}$$

The sum of the minima can be performed in the SSE registers several minima at a time. Similarly, the computation of $\sum _{j=1}^m\varvec{\mathbf {\mu }}_j^{(0)} \varvec{\mathbf {\sigma }}_j + \epsilon$ for all suitable $(\varvec{\mathbf {\sigma }},\epsilon )$ pairs identified at the beginning of a bundle method consists mainly of a dot product. This operation can be performed by the BLAS function ddot, and recent implementations of BLAS will perform several products simultaneously.

The generation of the subgradient $\varvec{\mathbf {\sigma }}^{(t)}$ was specified earlier as follows:

$$\begin{aligned} \forall j \in \{1,\ldots ,m\}, \quad \varvec{\mathbf {\sigma }}^{(t)}_j \leftarrow \,1 - \left| \left\{ i \in \{1,\ldots ,n\}: \underline{\varvec{\mathbf {x}}}_i^{(t)}= 1, \varvec{\mathbf {s}}_{ij} < \varvec{\mathbf {\mu }}_j^{(t)}\right\} \right| , \end{aligned}$$

but can be rewritten using the following vectors $\varvec{\mathbf {v}}^i \in \{0,1\}^m$, $i \in \{1,\ldots ,n\}$:

$$\begin{aligned} \varvec{\mathbf {\sigma }}^{(t)}\leftarrow (1, 1, \ldots , 1) - \sum ^n_{\begin{array}{c} i=1 \\ \underline{\varvec{\mathbf {x}}}_i^{(t)}= 1 \end{array}} \varvec{\mathbf {v}}^i, \end{aligned}$$

$$\begin{aligned} \text { with } \forall i \in \{1,\ldots ,n\}, \forall j \in \{1,\ldots ,m\}, \; \varvec{\mathbf {v}}^i_j = {\left\{ \begin{array}{ll} 1 &{} \text {if } \varvec{\mathbf {s}}_{ij} < \varvec{\mathbf {\mu }}_j^{(t)}, \\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Using SSE registers, we can compute several components of a vector $\varvec{\mathbf {v}}^i$ simultaneously.