Skip to main content

Advertisement

SpringerLink
Log in

Quasi-uniform stability of Caputo-type fractional-order neural networks with mixed delay

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

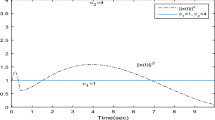
In this paper, a class of Caputo-type fractional-order neural networks with mixed delay is introduced. By employing known inequalities, such as Hölder inequality, Cauchy–Schwartz inequality and Gronwall inequality, sufficient conditions are presented to ensure that such neural network is quasi-uniformly stable. Finally, a numerical example is presented to prove the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Chua LO (1971) Memristor—the missing circut element. IEEE Trans Circuit Theory 18:507–519

    Article  Google Scholar 

  2. Strukov DB, Snider GS, Stewart DR, Williams RS (2008) The missing memristor found. Nature 453:80–83

    Article  Google Scholar 

  3. Tour JM, He T (2008) Electronics: the fourth element. Nature 453:42–43

    Article  Google Scholar 

  4. Podlubny I (1999) Fractional differential equations. Academic, New York

    MATH  Google Scholar 

  5. Butzer PL, Westphal U (2000) An introduction to fractional calculus. World Scientific, Singapore

    Book  MATH  Google Scholar 

  6. Hilfer R (2001) Applications of fractional calculus in physics. World Scientific, Hackensack

    MATH  Google Scholar 

  7. Kilbas AA, Srivastava HM, Trujillo JJ (2006) Theory and application of fractional differential equations. Elsevier, Amsterdam

    MATH  Google Scholar 

  8. Song L, Xu SY, Yang JY (2010) Dynamical models of happiness with fractional order. Commun Nonlinear Sci Numer Simul 15(3):616–628

    Article  MathSciNet  MATH  Google Scholar 

  9. R.C. Gu, Y. Xu (2011) Chaos in a fractional-order dynamical model of love and its control. In: Li SM, Wang X, Okazaki Y, Kawabe J, Murofushi T, Li G (eds) Nonlinear mathematics for uncertainty and its applications. AISC, Springer, pp 349–356, 881–886

  10. Arena P, Caponetto R, Fortuna L, Porto D (1998) Bifurcation and chaos in noninteger order cellular neural networks. Int J Bifurc Chaos 8(7):1527–1539

    Article  MATH  Google Scholar 

  11. Lundstrom BN, Higgs MH, Spain WJ, Fairhall AL (2008) Fractional differentiation by neocortical pyramidal neurons. Nat Neurosci 11(11):1335–1342

    Article  Google Scholar 

  12. Chon KH, Hoyer D, Armoundas AA (1999) Robust nonlinear autoregressive moving average model parameter estimation using stochastic recurrent artificial neural networks. Ann Biomed Eng 27(4):538–547

    Article  Google Scholar 

  13. Raol JR (1995) Parameter estimation of state space models by recurrent neural networks. IET Control Theory A 142(2):114–118

    Article  MATH  Google Scholar 

  14. Beer RD (2006) Parameter space structure of continuous-time recurrent neural networks. Neural Comput 18(12):3009–3051

    Article  MathSciNet  MATH  Google Scholar 

  15. Huang H, Huang TW, Chen XP (2013) A mode-dependent approach to state estimation of recurrent neural networks with Markovian jumping parameters and mixed delays. Neural Netw 46:50–61

    Article  MATH  Google Scholar 

  16. Wu A, Zhang J, Zeng Z (2011) Dynamic behaviors of a class of memristor-based Hopfield networks. Phys Lett A 375:1661–1665

    Article  MathSciNet  MATH  Google Scholar 

  17. Wen S, Zeng Z, Huang T Dynamic behaviors of memristor based delayed recurrent networks. Neural Comput Appl. doi:10.1007/s00521-012-0998-y

  18. Zhang G, Shen Y (2013) Global exponential periodicity and stability of a class of memristor-based recurrent neural networks with multiple delays. Inform Sci 232:386–396

    Article  MathSciNet  MATH  Google Scholar 

  19. Wu H, Zhang L (2013) Almost periodic solution for memristive neural networks with time-varying delays. J Appl Math, V, Article ID 716172, p 12. http://dx.doi.org/10.1155/2013/716172

  20. Zhang R, Qi D, Wang Y (2010) Dynamics analysis of fractional order three-dimensional Hopfield neural network. In: International conference on natural computation, pp 3037–3039

  21. Zhou S, Li H, Zhu Z (2008) Chaos control and synchronization in a fractional neuron network system. Chaos Solitons Fractals 36:973–984

    Article  MathSciNet  MATH  Google Scholar 

  22. Zhu H, Zhou S, Zhang W (2008) Chaos and synchronization of time-delayed fractional neuron network system. In: The 9th international conference for Young computer scientists, pp 2937–2941

  23. Zhou S, Lin X, Zhang L, Li Y (2010) Chaotic synchronization of a fractional neurons network system with two neurons. In: International conference on communications, circuits and systems, pp 773–776

  24. Zhao HY, Wang L, Ma CX (2008) Hopf bifurcation and stability analysis on discrete-time Hopfield neural network with delay. Nonlinear Anal Real World Appl 9:103–113

    Article  MathSciNet  MATH  Google Scholar 

  25. Zhao HY, Wang L (2006) Stability and bifurcation for discrete-time CohenCGrossberg neural network. Appl Math Comput 179:787–798

    MathSciNet  MATH  Google Scholar 

  26. Chen L, Chai Y, Wu R, Ma T, Zhai H (2013) Dynamic analysis of a class of fractional-order neural networks with delay. Neurocomputing 111:190–194

    Article  Google Scholar 

  27. Li CP, Deng WH (2007) Remarks on fractional derivatives. Appl Math Comput 187:777–784

    MathSciNet  MATH  Google Scholar 

  28. Mitrinovic DS (1970) Analytic inequalities. Springer, New York

    Book  MATH  Google Scholar 

  29. Kuczma M (2009) An introduction to the theory of functional equations and inequalities: Cauchy’s equation and Jensen’s inequality. Birkhauser, Switzerland

    Book  MATH  Google Scholar 

  30. Corduneanu C (1971) Principles of differential and intergral equations. Allyn and Bacon, USA

    MATH  Google Scholar 

Download references

Acknowledgments

The authors are extremely grateful to anonymous reviewers for their careful reading of the manuscript and insightful comments, which help to enrich the content. We would also like to acknowledge the valuable comments and suggestions from the editors, which vastly contributed to improve the presentation of this paper.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Yanshan University, Qinhuangdao, 066004, China

    Huaiqin Wu, Xinxin Zhang & Shunhui Xue

  2. School of Electrical Engineering, Yanshan University, Qinhuangdao, 066001, China

    Peifeng Niu

Authors
  1. Huaiqin Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xinxin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shunhui Xue
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Peifeng Niu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Huaiqin Wu.

Additional information

This work was jointly supported by the National Natural Science Foundation of China (61573306), the Postgraduate Innovation Project of Hebei province of China (00302-6370019) and High level talent support project of Hebei province of China (C2015003054).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, H., Zhang, X., Xue, S. et al. Quasi-uniform stability of Caputo-type fractional-order neural networks with mixed delay. Int. J. Mach. Learn. & Cyber. 8, 1501–1511 (2017). https://doi.org/10.1007/s13042-016-0523-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-016-0523-1

Keywords

Search

Navigation