1 Introduction

Sparsity is crucial to a variety of real-world applications due to its importance in detection, classification, decision, and signal reconstruction [1,2,3,4,5,6,7,8,9]. Therefore, sparse signal learning (SSL) has been a hot research topic in the field of machine learning, information theory, signal processing and computer vision [8,9,10,11], etc. The sparse signal learning is essentially a sparse solution optimization problem, which can be solved by the gradient or subgradient descend method. Currently, majority of studies mainly embroider on a central issue, namely how to develop highly effective algorithm for sparse signal learning. The mainstream of current learning algorithms for SSL in the literature are the convex optimization methods using \(l_1\)-norm constraints [12,13,14,15,16](e.g., the basis pursuit method [12, 15, 16]). The \(l_1\)-norm-based methods are effective by using various convex optimization techniques, while, these methods usually approach to approximate solution due to that the objective function is a combination of \(l_1\)-norm and constrictions. Some other methods are also proposed as complementary strategies, including the heuristic orthogonal matching pursuits (OMP) [17] for constructing the support index set step by step, and the Bayesian method [18] that uses the posterior probability for matching the observation data derived from sparse prior probability, and so forth. The heuristic orthogonal matching pursuit (OMP) methods are simple for implementation, while the accuracy is relatively lower than other methods (say, \(l_1\)-nom-based methods). The Bayesian method is an effective algorithm for recovery, while the relevant matrix computation is generally close to singular cases and thus is numerically unstable.

Based on the convex theory, a remarkable convex learning algorithm is developed in [14,15,16] by using the standard optimization techniques, e.g., logarithm barrier function for relaxing the constraints and Newtonian step for searching optimal value. The authors also developed effective Matlab toolbox named ‘l1magic’ for demonstration and simple application. However, these algorithms require many iterations to approximate the genuine solution and thus they are generally time-consuming especially for high dimension cases. Moreover, the conditions required for convergence are very restricted for the given measurement matrix. Recently, the so-called iterative shrinkage-thresholding algorithm (ISTA) gradually becomes a popular method for solving SSL by using the proximal gradient approximation technique, which makes that each iteration of ISTA involves only matrix–vector multiplication followed by a shrinkage/soft-threshold step [19,20,21,22,23,24]. The objective function of ISTA or FISTA is a mixing weighted sum of 1-norm and 2-norm, which results in that the learning of the exact source sparse signal cannot be guaranteed. To facilitate the application of ISTA in large scale problem, a refined version called fast ISTA (FISTA) was proposed in [25] based on the Nesterov’s speeding technique [26]. An essentially equivalent Bregman iteration method, by replacing the objective function with simple quadratic function, was also presented in [27,28,29] and analyzed by various background knowledge. The iteration process of the above mentioned methods with easy calculation is simple but very effective. However, this kind of algorithms generate approximate estimation to the genuine sparse signal, since the objective function has been partially replaced by some other components with simple gradient. Hence, inevitably it requires many iterations to derive accurate estimation.

Some latest algorithms regarding SSL combining above techniques are listed as follows. An alternating projection (AP) method was proposed and analyzed in [30]. This method is simple for implementation while the hard threshold operator step is a shortcoming, which makes unsatisfactory signal recovery rate. A method using Shannon entropy function (SEF) was proposed in [32] by applying the refined multiple proximal gradient approximation techniques. However, since the entropy function is not a convex function, this method highly depends on the initial point of iteration. A belief propagation-based method was proposed in [33] to learn clustered signal (image), rather than general sparse signal. Moreover, the whole learning process is complicated and uneasy for theoretical analysis. An Iterative Proximal Projection (IPP) method was proposed in [34] using proximal gradient approximation technique. Since it is still an approximation method, it requires many and sufficient iteration to approach the genuine solution. Theoretical analysis regarding \(l_p\)-norm \((0<p<1)\) optimization framework for sparse signal learning was presented in [35]. However, effective algorithm to implement the non-convex \(l_p(0<p<1)\) optimization seems few.

Aiming at building a concise and efficient model for sparse signal learning, this work develops a direct method based on simple observation of subgradient of the 1-norm function \(\Vert x\Vert _1\) for a vector \(x\in R^n\). It is observed that the 1-norm function \(\Vert x\Vert _1\) is differentiable at any point with all its coordinates nonzero, which is called a regular point for simplicity. Hence, at a regular point, the 1-norm objective function can easily derive a decreasing search direction by using its reverse gradient for sparse signal learning. At an irregular point (some coordinates are zeros), the 1-norm function \(\Vert x\Vert _1\) owns subgradient, which can still provide information to construct decreasing search direction for the learning purpose. An immediate problem is how to select a suitable subgradient to construct decreasing direction. It is observed that an irregular point can be viewed as a regular point in a restricted subspace. For example, let \(\xi =[\xi _1,\xi _2,0]\in R^3\) with nonzero \(\xi _1\) and \(\xi _2\). It is clear shown by [46] that the subgradients of \(\Vert x\Vert _1\) at point \(\xi\) is the set of vectors \(\{[\text{ sign }(\xi _1),\text{ sign }(\xi _2),\epsilon ], |\epsilon |\le 1\}\). Note that the subspace \(V_2{\mathop {=}\limits ^{\Delta }}\{[\eta _1,\eta _2,\eta _3]\in R^3|\eta _3=0\}\) contains only one subgradient of \(\xi\), i.e., \(\text{ grad }(\xi ){\mathop {=}\limits ^{\Delta }}[\text{ sign }(\xi _1),\text{ sign }(\xi _2),0]\), thus the irregular point \(\xi\) in \(R^3\) can be viewed as a regular point in the subspace \(V_2\) with unique gradient \(\text{ grad }(\xi )\). Therefore, the restricted subgradient in suitable subspace can act as common case to derive decreasing search direction. Naturally, for a linearly restricted optimization problem, the suitable subspace to be considered is derived by the given linear constraints.

It is clear by the above observations that a deceasing direction of objective function \(\Vert x\Vert _1\) can be easily constructed by the restricted projection of the subgradient to the subspace spanning by restriction equations, for an irregular point with the number of its nonzero components larger than the number of restriction equations. Next let us show how to construct feasible search direction of objective function \(\Vert x\Vert _1\) for sparse signal learning by taking into account the gradient/subgradient information. Without loss of generality, suppose the iteration starts at a regular point \(x_0\in R^n\) by giving measurement matrix \(A\in R^{m\times n}\) and setting \(m<n\). A good initial point can be set by the least squares estimation, which may probably locate in the same hyperoctant of the minimal 1-norm solution. The gradient of \(x_0\) is firstly projected to the null space of matrix A, which is the feasible search direction to guarantee the restriction, i.e., the observation equation \(y=Ax\). Then, by searching the reverse direction of the projected gradient (projection to the null space of matrix A), an irregular point \(x_1\) with 1-component zero is achieved, since the minimal 1-norm value may not be attained in a regular point if the minimum is unique. To use the subgradient of \(x_1\) for next iteration, the search direction is restricted in the \((n-1)\) dimensional subspace according to the support index set of \(x_1\). The point \(x_1\) can be viewed as a regular point in this subspace, its restricted gradient in the subspace (comprised of the \((n-1)\) support components of \(x_1\)) can be projected to the restricted null space of the restricted sub-matrix of A (comprised of the \((n-1)\) support components of \(x_1\)) to construct a decreasing direction for the 1-norm function. By searching the reverse direction of the projected gradient in this subspace, an irregular point \(x_2\) is derived with 2-component zero. This process continues at most \((n-m)\) iterations, an vertex with \((n-m)\) zero components is derived. A naive projection algorithm is proposed by using purely restricted projection.

However, the restricted projection at a vertex of the feasible set may be reduced to a zero matrix and thus fails to update the next iteration. A refined learning algorithm-based on the restricted projection is then developed by checking the subgradient condition to find whether the optimal solution is achieved. The subgradient condition (described in Sect. 2) is a minimum condition for successful signal recovery. If the optimal solution is not arrived, then a new search direction is constructed using linear equation theory. This step is described in Sect. 4, which may be viewed as a similarity and generation of the pivot step in simplex algorithm. Since the vertices are finite and the 1-norm value decreases strictly for each iteration, the proposed model can accurately find the minimum in finite iteration.

In brief, there are two main steps of the proposed sparse signal learning method: one is the restricted projection and second is checking subgradient condition and construction of new potential search direction by the checking. The main theoretical result of this paper is Theorem 3.1, which is a convergence analysis of the proposed method. The main technical contributions of this paper are as follows:

(i) A novel restricted projection technique is developed to iteratively derive a vertex of the feasible solution set for the optimal value learning issue with regard to 1-norm-based model;

(ii) An optimal sparse solution detection and learning method at a vertex is proposed by checking whether the subgradient condition is satisfied, meanwhile the accuracy of sparse signal learning can be improved;

(iii) An improved search direction is constructed at a vertex by using the information of subgradient condition checking, which greatly improves the efficiency of sparse signal learning.

The rest of the paper is organized as follows. Section 2 presents the problem statement and sufficient and necessary conditions for successful signal recovery by convex algorithms. A new subgradient descend method is developed and analyzed in Sect. 3, where Theorem 3.1 is the main theoretical result of this paper. A deterministic construction method for the measurement matrix satisfying the subgradient condition is proposed in Sect. 4. Numerical simulation is tested in Sect. 5 to verify the established theoretical assertions. Finally, Sect. 6 concludes the paper.

2 Framework and Related Works

For sparse signal learning (SSL) problem, a standard observation model can be described as

$$\begin{aligned} y=A{x}, \end{aligned}$$
(1)

where the measurement vector \(y \in R^m\) can be linearly represented by n basis vectors contained in measurement matrix \(A \in R^{m\times n}\), and k sparse signal \(x \in R^{n} (k<m<n)\) indicates that only k elements are nonzero in x. The central task of SSL aims at learning x for a variety of signal processing and machine learning purposes.

The choice of regularization norm will lead to different versions of SSL model. In an ideal case, \(l_0\)-norm will produce an original framework of SSL problem, namely the combination optimization

$$\begin{aligned} (P_0)\quad \min _{x}\Vert x\Vert _0 \text{ s.t. } Ax=y, \end{aligned}$$
(2)

where \(\Vert x\Vert _0\) tries to punish the number of non-zeros signal in x. However, such a \(l_0\)-norm-based model is NP-hard [36] and is very difficult to optimize in real-world applications. By replacing \(l_0\)-norm with \(l_1\)-norm, model (2) can be furthered relaxed as a convex version

$$\begin{aligned} (P_1)\quad \min _{x}\Vert x\Vert _1 \text{ s.t. } Ax=y, \end{aligned}$$
(3)

where \(l_1\)-norm punishes the sum of all the sparse signal components. In the view of optimization, the solution of model (3) can be regarded as Basis Pursuit (BP) [12]. Recent studies [15, 16] have provided a variety of techniques to solve this problem. However, the algorithms lying in these techniques normally rely on very restrictive conditions to achieve convergence [38].

The optimization framework for the popular ISTA and FISTA algorithms [25] is built on a summation of mixed norms \(\Vert \cdot \Vert _1\) and \(\Vert \cdot \Vert _2\):

$$\begin{aligned} \min _{x}\ \mu \Vert x\Vert _1+\frac{\delta }{2}\Vert y-Ax\Vert _2^2, \end{aligned}$$
(4)

where \(\Vert \cdot \Vert _2\) is the Euclidean norm for a vector and \(\mu\) and \(\delta\) are two positive real numbers. The ISTA algorithm is proposed by using proximal regularization technique (the term \(\Vert y-Ax\Vert _2^2\) in objective function is replaced by its first two Taylor series at present estimation \(x_k\) to derive next estimation) in iteration. FISTA is a refined version of ISTA using the Nesterov’s speeding technique [26]. Although ISTA and FISTA [25] are two effective algorithms for solving model (4) with easy iteration calculation, the exact solution of the objective function (4) is different from the genuine sparse solution satisfying the observation equation (3). Only when the parameter \(\mu\) is sufficiently small and parameter \(\delta\) is sufficiently large, the exact solution of (4) can approximate the solution of (3) to certain extent. Another effective algorithm called Bregman method [27], essentially the same of ISTA, is proposed based on Bregman distance. The performance of Bregman method is quite similar to ISTA algorithm, as shown in the following numerical experiments.

The existing problem of optimization framework (4) is that it normally needs a large quantity of iteration times to achieve its solution, and such a solution may not belong to the solution space of \((P_1)\). In this paper, we aim to take the advantages of gradient/subgradient information of function \(\Vert x\Vert _1\) to develop effective algorithm to obtain the exact solution of the optimization framework \((P_1)\) in finite iteration steps for sparse signal learning.

The objective function (4) is more likely to be applied in real application due to inevitable noise disturbance. Yet, if the exact recovery issue \((P_1)\) can be recovered more accuracy, the problem (4) may be solved more effectively. The extension of the proposed method to objective (4) is left for later consideration.

2.1 Sufficient and necessary condition for optimality

In this subsection, we demonstrate the minimal condition to derive a point with minimum 1-norm value for a certain convex algorithm. A sufficient and necessary condition for the uniqueness of solution for \((P_1)\) was proposed in [37], where one assumption on the measurement matrix can be reduced. Its simplified version (called subgradient condition) as listed below has been proved in [38] in a geometric way by using related subgradient theory.

Theorem 2.1

For a given k-sparse solution \(\bar{x}\) of \((P_1)\), denote its support index set by S. Then, a sufficient and necessary condition for the uniqueness of the solution \(\bar{x}\) to \((P_1)\) is that: the rank of matrix \(A_S\) is k, and there exists \(\lambda \in R^m\) such that \(A_S^T\lambda =\text{ sign }(\bar{x}_S)\) and \(\Vert A_{S^c}^T\lambda \Vert _{\infty }<1\).

Here the set \(S^c\) is the complementary set of S in \(\{1,2,\ldots ,n\}\). The matrix \(A_S\) means a matrix with the columns of A restricted in the index set S, i.e., \(A_S=A[:,S]\). The assumption of matrix A with full row rank in [37] has been reduced to the condition that the rank of matrix \(A_S\) is k. It is shown in [38] that this subgradient condition is much weaker than the well-known null space property (NSP) condition [39, 40, 42], since the NSP condition deals with any sparse signal with sparsity k, while the subgradient condition deals with a particular given k-sparse signal. The restricted isometry property (RIP) [14, 41, 43] and mutual coherence condition [13, 44, 45] are much stronger than the NSP condition, as shown in [38]. Therefore, the subgradient condition is the minimal requirement for the uniqueness of the optimization framework \((P_1)\). In other words, the subgradient condition is the bottom line for \((P_1)\), and it is believed that it is also the bottom line for any convex algorithm for SSL, due to that the objective function of SSL generally contains the 1-norm penalty to derive sparse solution, as shown in (4).

2.2 Sufficient condition for optimality

Let us recall briefly the notion subgradient for further development. For a convex function \(f(\cdot ): R^n\rightarrow R\), a vector \(\mu \in R^n\) is called a subgradient [46] of \(f(\cdot )\) at a point x if

$$\begin{aligned} f(z)-f(x)\ge \mu ^T(z-x) \end{aligned}$$
(5)

for any \(z\in R^n\).

For the function \(f(x)=\Vert x\Vert _1\), the set of its subgradients at a sparse point x is

$$\begin{aligned} \partial f(x)=\{\mu :\ \mu _i=\text{ sign }(x_i),\ i\in S;\ \mu _j\in [-1,1], \ j\in S^c\}, \end{aligned}$$
(6)

where S is the support set of x.

It is worth noting that the main subgradient condition \(\Vert A_{S^c}^T\lambda \Vert _{\infty }<1\) in Theorem 2.1 is in terms of strict inequality and it cannot be extended to include the equality case. When the subgradient condition is relaxed slightly to allow equality \(\Vert A_{S^c}^T\lambda \Vert _{\infty }\le 1\), it is still able to conclude that the point is a minimum of \((P_1)\), while the uniqueness may be lost. In other words, under this case, there may be some other minimal solutions for problem \((P_1)\) and the generalized condition is reduced to be a sufficient condition for minimum. Precisely, the following statement specifies the generation to include the equality case.

Theorem 2.2

For a given solution \(\bar{x}\) of \((P_1)\), denote its support index set by S. If there exists \(\lambda \in R^m\) such that \(A_S^T\lambda =\text{ sign }(\bar{x}_S)\) and \(\Vert A_{S^c}^T\lambda \Vert _{\infty }\le 1\). Then, the solution \(\bar{x}\) is a minimal solution of \((P_1)\).

The above result can be easily proved by Proposition B.24 of [47], and thus is omitted here.

Let us show that the \(l_1\) minimal solution of \((P_1)\) may not be unique by two simple examples. Let the measurement matrix be \(A=[1,1,1]\) and \(x=[1, 0, 0]^T\), then the whole simplex \(\{x\in R^3| x_1+x_2+x_3=1,x_i\ge 0,i=1,2,3\}\) are all the \(l_1\) minimal solutions. If \(A=[1,1/2,1]\) and \(x=[1, 0, 0]^T\), then the whole line segment \(\{x\in R^3| x_1+x_3=1,x_1\ge 0,x_3\ge 0\}\) are all the \(l_1\) minimal solutions. Under both cases, it is clear that the generalized subgradient condition of Theorem 2.2 is satisfied for any \(l_1\) minimal solution. Thus, it is better to develop algorithms to satisfy the subgradient condition (rather than the generalized version) for searching the unique minimal 1-norm solution.

3 Subgradient descend algorithms

The SSL optimization issue \((P_1)\) given by (3) can be solved in various ways, e.g., ISTA (Bregman) or FISTA method with objective function replaced by (4). However, as mentioned in Sect. 2, these approximation frameworks fail to derive the exact genuine sparse solution of \((P_1)\). There exists also optimization methods to solve \((P_1)\) in an exact way, e.g., using the existing simplex algorithm. However, it is well-known that the simplex algorithm performs worse for high dimension case and there are examples to show that The iteration times of simplex algorithm with pivot step turn to be exponential growth in the worst case.

In this section, we propose a direct recovery method for SSL issue \((P_1)\) to derive the optimal sparse solution in finite iteration steps. The method uses the gradient/subgradient of function \(\Vert x\Vert _1\) to derive a search direction at each iteration step. Note that the 1-norm function \(\Vert x\Vert _1\) for vector \(x\in R^n\) is differentiable for any regular point (not located on some coordinate axes, i.e., all its coordinates are nonzero). Thus a decreasing direction can be easily constructed at a regular point. For an irregular point, if it is restricted to subspace corresponding to its support index set, then it turns to be a regular point in this subspace, and thus a decreasing direction can be easily constructed. When the irregular point has \(n-m\) or even more zero components, particular pivoting search direction is constructed by using the subgradient information, which will be described in the refined version of the proposed method.

Let us introduce some notations to facilitate further presentation. For a vector \(\xi \in R^n\), denote its i-th component by \(\xi [i]\). For an index set \(S\subset \{1,\ldots ,n\}\), we use \(\xi [S]\) to denote its sub-vector comprised of the components’ index belonging to S. For a matrix \(A\in R^{m\times n}\), denote its submatrix comprised of columns with their indices belonging to an index set S by A[ : , S]. Given an index set S, denote \(A_S\) as the submatrix of A formed by its columns \(a_i\), \(i\in S\), and \(x_S\) as the subvector of x formed by entries \(x_i\), \(i\in S\). Denote the Euclidean norm and maximum norm of vector by \(\Vert \cdot \Vert _2\) and \(\Vert \cdot \Vert _{\infty }\) respectively.

The feasible set (the collection of points with the restriction satisfied) is defined by

$$\begin{aligned} F{\mathop {=}\limits ^{\Delta }}\{x\in R^n: Ax=y\}, \end{aligned}$$
(7)

which is obviously convex and its boundary are flat since it is constructed by the intersection of finite hyperplanes. A vertex of F is defined as a point \(\xi \in F\) such that \(\xi\) have \((n-m)\) zero components. Any feasible search direction obviously belongs to the null space of matrix A, namely \(\mathcal {N}(A)=\{\eta \in R^n|A\eta =0\}\).

Suppose the matrix A is full of row rank for simplicity. Actually the rank requirement can be relaxed to the corresponding part of Theorem 2.1. Let us call a point \(x\in R^n\) is regular if x has no zero components. Let us start the algorithm from the least squares estimation

$$\begin{aligned} x_0=A^T(AA^T)^{-1}y. \end{aligned}$$
(8)

It is shown in [48, 49] that for any vector \(\xi \in R^n\), there are inequalities between 1-norm and 2-norm as follows:

$$\begin{aligned} \Vert \xi \Vert _2\le \Vert \xi \Vert _1\le \sqrt{n}\Vert \xi \Vert _2. \end{aligned}$$
(9)

Hence, if it starts from point \(x_0\) to find minimal 1-norm point, the radius centered in \(x_0\) for searching is

$$\begin{aligned} r=\sqrt{n-1}\Vert x_0\Vert _2. \end{aligned}$$
(10)

Indeed, for any \(\eta \notin B(x_0,r)\), it follows that \(\Vert \eta \Vert _1\ge \Vert \eta \Vert _2\ge \sqrt{n}\Vert x_0\Vert _2\ge \Vert x_0\Vert _1\), which implies the possible minimal 1-norm point can only locate in \(B(x_0,r)\).

The gradient of 1-norm function \(\Vert x\Vert _1\) at a regular point is

$$\begin{aligned} d_0=\text{ sign }(x), \end{aligned}$$
(11)

where the sign is with respect to each components of x.

For matrix \(A\in R^{m\times n}\), recall the corresponding projection operator to the null space of matrix A, we have

$$\begin{aligned} Pr(A)=I_n-A^T(AA^T)^{-1}A, \end{aligned}$$
(12)

where \(m\le n\). The projected gradient of function \(\Vert x\Vert _1\) at a regular point and its normalized version respectively are given by

$$\begin{aligned}&\bar{d}=Pr(A)d_0, \end{aligned}$$
(13)
$$\begin{aligned}&d=\bar{d}/\Vert \bar{d}\Vert _2. \end{aligned}$$
(14)

As mentioned in the beginning of this section, the method is divided into two cases. The first case studies a regular point or an irregular point with more than m nonzero components; and the other case studies an irregular point with equaling or less than m nonzero components. The search direction is constructed by using the projected gradient in a suitable subspace of \(R^n\) for the first case. A naive algorithm is developed by purely using projection to find the minimal estimation, which will be explained in the following subsection 3.1 and it will be treated cautiously in a refined version to construct a pivoting direction by using the subgradient information in subsection 3.2.

Fig. 1
figure 1

The evolution processes of Examples 3.1 and 3.2. a Example 3.1: starting at \(\tilde{x}_0=[0.5,1,0]^T\), then by projected gradient \(d_1\) moving to \(\tilde{x}_1=\left[ \frac{1}{2}+\frac{5}{49},\frac{27}{49},\frac{18}{49}\right] ^T\), whose \(l_1\)-norm increases; while by restricted projected gradient \(d_2\) moving to \(\tilde{x}_2=\left[ 0.7,0.6,0\right] ^T\), whose \(l_1\)-norm decreases. b Example 3.2: starting at \(x_0=[0.44,0.88,0.36]^T\), by projected gradient \(d_0\) moving to \(x_1=\left[ 2/3,2/3,0\right] ^T\), and then by restricted projected gradient \(d_1\) moving to \(x_2=[1,0,0]^T\), which is the unique minimal \(l_1\)-norm solution of the measurement equation

Full size image

A key issue for an effective algorithm is how to design a feasible search direction for an irregular point (i.e., point with some components being zero). The subgradients of an irregular point can be projected to certain suitable subspace so as to derive feasible search direction. The following example demonstrates how to construct a restricted projection to find a feasible direction.

Example 3.1

For the measurement equation \(x[1]+x[2]/2+x[3]/3=1\), the measurement matrix is \(A=[1, 1/2, 1/3]\). Consider \(\tilde{x}_0=[1/2,1,0]^T\), the projection direction of \(\text{ sign }(\tilde{x}_0)\) to the null space of A is \(d_1=1/49[-5,22,-18]^T\). Thus, the move of \(\tilde{x}_0\) along the reverse subgradient of d with step 1 is given by

$$\begin{aligned} \tilde{x}_1=\tilde{x}_0-d_1=\left[ \frac{1}{2}+\frac{5}{49},\frac{27}{49},\frac{18}{49}\right] ^T, \end{aligned}$$
(15)

which clearly implies that \(\Vert \tilde{x}_1\Vert _1=\frac{3}{2}+\frac{1}{49} >\Vert \tilde{x}_0\Vert _1=\frac{3}{2}\). However, if the consideration is restricted in subspace \(V=\{x\in R^3|x_3=0\}\), the projection direction of \(\text{ sign }(\tilde{x}_0[1,2])\) to the null space of matrix \(A[1,2]=[1,1/2]\) is \(d_2=1/5[-1,2]^T\). Thus, the move of \(\tilde{x}_0[1,2]\) along the reverse gradient of \(d_2\) with step 1 in the subspace V is given by

$$\begin{aligned} \tilde{x}_2[1,2]=\tilde{x}_0[1,2]-d_2=\left[ \frac{7}{10},\frac{3}{5}\right] ^T, \end{aligned}$$
(16)

where \(\tilde{x}_2[3]=0\) since \(\tilde{x}_2\in V\). Clearly \(\Vert \tilde{x}_2\Vert _1=\frac{13}{10}<\Vert \tilde{x}_0\Vert _1=\frac{3}{2}\). The evolution process is shown in Fig. 1a. For the point located in line \(Q_xQ_y\), the restricted projected gradient is parallelling to the line \(Q_xQ_y\), which make the update move along the line \(Q_xQ_y\).

The first part of the above Example 3.1 tells us that the projected direction may not be feasible if the gradient is not projected to the restricted subspace. However, if we project the subgradient \(\text{ sign }(\tilde{x}_0[1,2])\) to the restricted subspace V, the derived projection is a feasible search direction. This example suggests that the restricted projection is a good way to derive a k-sparse solution if the iteration point possesses more than k nonzero components. It is worth pointing that the projection of such subgradient is still the increasing direction for 2-norm in the above example.

3.1 Naive subspace projection algorithm for SSL

A simple way to find the k-sparse solution of \((P_1)\) is to perform the restricted projection until it derives a k-sparse solution. To demonstrate the intuitive idea of this naive algorithm, let us show a simple example to describe the main scheme of restricted projection to learn the sparse solution of issue \((P_1)\).

Example 3.2

For the measurement equation \(x[1]+x[2]/2+x[3]/3=1\), to learn the solution of \((P_1)\), i.e., min \(\Vert x\Vert _1\).

The measurement matrix is \(A=[1, 1/2, 1/3]\). Consider \(x_0=[0.44,0.88,0.36]^T\), the projection direction of \(\text{ sign }({x})\) to the null space of A is \(d_0=1/49[-17,16,27]^T\). Thus, the move of \(x_0\) along the reverse gradient of \(d_0\) with step \(\lambda _0=49/75\) is given by

$$\begin{aligned} x_1=x_0-\lambda _0d_0=\left[ 2/3,2/3,0\right] ^T. \end{aligned}$$
(17)

Clearly \(\Vert x_1\Vert _1<\Vert x_0\Vert _1\). Next, restrict the consideration in the subspace \(V=\{x\in R^3|x[3]=0\}\), the projection direction of \(\text{ sign }(x_1[1,2])\) to the null space of matrix \(A[1,2]=[1,1/2]\) is \(d_1=1/5[-1,2]^T\). Thus, the move of \(x_1[1,2]\) along the reverse gradient of \(d_1\) with step \(\lambda _1=5/3\) in the subspace V is given by

$$\begin{aligned} x_2[1,2]=x_1[1,2]-\lambda _1d_1=\left[ 1,0\right] ^T, \end{aligned}$$
(18)

where \(x_2[3]=0\) since \(x_2\in V\). It is clear that the derived point \(x_2=[1,0,0]^T\) is the unique minimal \(l_1\)-norm solution of the measurement equation. The evolution process is shown in Fig. 1b.

In the above Example 3.2, two projections of decreasing directions to suitable subspace are implemented to derive feasible search directions. The measurement matrix A is of size \(1\times 3\), whose null space is a 2-dimension subspace of \(R^3\). The starting point is a regular point of \(R^3\), whose components are all nonzero. The derived point \(x_1\) possesses two nonzero components, whose gradient restricted in subspace \(\{(\xi _1,\xi _2,0),\xi _1,\xi _2\in R\}\) can be projected to the null space of sub-matrix A( : , [1, 2]). The geometric meaning of the second step is to move the solution along the straight line \(x[1]+x[2]/2=1\) over the xoy plane from point \(x_1\) to \([1,0,0]^T\). It is lucky under this example that the minimal solution has been derived by two iterations using projected search directions.

Now let us summarize the main steps of the naive projection algorithm in details.

(i) Dimension reduction to a vertex by restricted projection.

Let \(x_0\) be a feasible solution, i.e., \(x_0\in F\). Now, let us consider a move along the direction of \(-d\) by a step length \(\alpha\) to derive

$$\begin{aligned} x_1=x_0-\alpha d \end{aligned}$$
(19)

such that \(x_1\in F\) are feasible points, where \(\alpha >0\). Since \(x_1\) is still a feasible point, it is clear that \(Ax_1=y\). Thus the step size \(\alpha >0\) is cautiously selected to make \(x_1\) be a point with minimal 1-norm and with 1 component zero. The potential step size is among the ratios \(\rho _i=\frac{x_0[i]}{d[i]}\) for \(i=1,\ldots ,n\), where \(x_0[i]\) denotes the i-th component of \(x_0\) and d[i] the i-th component of d. Denote

$$\begin{aligned} \bar{\rho }{\mathop {=}\limits ^{\Delta }}\text{ argmin}_{\rho _i}\left\{ \Vert x_0-\rho _id\Vert _1,\rho _i\in (0,2r),i=1,\ldots ,n\right\} , \end{aligned}$$
(20)

where r is defined by (10). Now update new estimation \(x_{1}\) by (19) with \(\alpha =\bar{\rho }\).

Suppose the minimum of (20) is attained at \(i_1\), which means that the \(i_1\)-th component of \(x_1\) is zero. If \(x_1\) is not the optimal solution, the next update of the point \(x_1\) may need some other directions, since the \(i_1\)-th component of \(x_1\) is already zero by the last update (19) using \(\alpha =\bar{\rho }\). Hence, we intend to further update this point by changing its other components while keeping the \(i_1\)-th component being zero, which can be done by projecting the vector \(d_0\) to a sub-polytope of F with \(x_{i_1}=0\). Denote an index set

$$\begin{aligned} S_1=\{1,2,\ldots ,n\}\backslash \{i_1\}. \end{aligned}$$
(21)

By discarding the \(i_1\)-th column of matrix A, an \(m\times (n-1)\) matrix \(A_1=A[:,S_1]\) is derived. A new projection matrix \(P_1=Pr(A_1)\) is defined by (12). Let \(x_2[i_1]=0\). The other components of \(x_2\) are updated from \(x_1[S_1]\) by

$$\begin{aligned} x_2[S_1]=x_1[S_1]-\alpha _1 d_1, \end{aligned}$$
(22)

where \(d_1=\bar{d}_1/\Vert \bar{d}_1\Vert _2\) and \(\bar{d}_1=P_1d_0[S_1]\). The selection of \(\alpha _1\) is similar to the selection process of \(\alpha\) in the above first update. Let the second selected index be \(i_2\) as in formula (20). Clearly, the \(i_1\)-th and \(i_2\)-th components of \(x_2\) are now zeros by the last update (22). By applying the above dimension reduction search idea, the next update is restricted on a sub-polytobe of F with \(x_{i_1}=0\) and \(x_{i_2}=0\). Continue this manner of dimension reduction by at most \(n-m\) steps, we arrive at a vertex of the polytope F with \(n-m\) zero components.

(ii) Update at a vertex.

At the end of the first strategy (i), a vertex, say \(x_t\), of the feasible set F is arrived. A subgradient at this point is \(\text{ sign }(x_t)\). The naive idea is still to use the restricted projection for deriving feasible search direction for next update as (19), although the derived feasible direction may be a zero vector under unlucky circumstances.

A detailed description of the proposed sparse signal learning algorithm is presented below.

Table 1 Naive Subspace Projection Algorithm
Full size table

Remark 3.1

In real application in numerical computation, the support index set \(S_t\) is comprised of the components with their absolute values less than an small threshold, say \(10^{-8}\), since there are inevitably truncation biases caused by numerical computation. The bias bound \(\epsilon\) is typically selected to be \(\epsilon =10^{-5}\).

The naive projection algorithm generally performs well, especially with the starting point being the least squares estimation. However, occasional divergence may occur even when the subgradient condition is satisfied. This is because that the reverse projection of subgradient onto the null space of matrix A may not be a decreasing direction of \(\Vert x\Vert _1\) at a vertex of F. The reason may be that the projection is constructed in terms of 2-norm rather than 1-norm for vectors.

Next we show a simple counter example for the failure of the naive projection algorithm to derive the sparsest solution of \((P_1)\).

Example 3.3

For the measurement equation \(x[1]+x[2]/2+x[3]/3=1\), the measurement matrix is \(A=[1, 1/2, 1/3]\). Consider \(\tilde{x}_0=[0,1,3/2]^T\), the projection direction of \(\text{ sign }(\tilde{x}_0)\) to the null space of A( : , [2, 3]) is \(d=1/13[-2,3]^T\). Thus, the move of \(\tilde{x}_0[2,3]\) along the reverse subgradient of d with step 13/2 is given by

$$\begin{aligned} \tilde{x}_1[2,3]=\tilde{x}_0[2,3]-13d/2=\left[ 2,0\right] ^T, \end{aligned}$$
(23)

which means \(\tilde{x}_1=[0,2,0]^T\). However, the restricted projection of subgradient \(\text{ sign }(\tilde{x}_1[2])\) to subspace \(\{[0,\xi ,0], \xi \in R\}\) is zero. Thus, the movement of naive projection algorithm finalizes at \(\tilde{x}_1\), rather than the minimal point [1, 0, 0].

Since the naive projection algorithm cannot guarantee to find the sparest solution, we develop the following refined version.

Fig. 2
figure 2

The evolution processes of Examples 3.3 and 3.4. (a) Example 3.3: starting at \(\tilde{x}_0=[0,1,3/2]^T\), then by projected gradient d moving to \(\tilde{x}_1=[0,2,0]^T\), whose \(l_1\)-norm decreases. While the restricted projection gradient at \(\tilde{x}_1\) is zero vector, which means that the naive projection method fails at \(\tilde{x}_1\), since \([1,0,0]^T\) is the minimum \(l_1\)-norm point. (b) Example 3.4: starting at \(\tilde{x}_0=[0,1,3/2]^T\), by projected gradient d in Example 3.3 moving to \(\tilde{x}_1=[0,2,0]^T\), and then using the constructed direction h (by checking subgradient condition) moving to \(\tilde{x}_2=[1,0,0]\), which is the unique minimal \(l_1\)-norm solution of the measurement equation

Full size image

3.2 Refined Projection Algorithm for Sparse Signal Learning

The drawback of the naive projection algorithm NSP is that the restricted projection by a vertex may be a zero vector, which is stated in step 2(ii) in Table  1. Note that the subgradient condition is a sufficient and necessary condition for issue \((P_1)\), let us now turn our attention to check whether the subgradient condition is attained at the derived vertex of the feasible set and find possible feasible direction by the information provided by the checking.

To demonstrate the intuitive idea for the refined projection algorithm, a simple example is presented below.

Example 3.4

(Continuing Example 3.3) For the measurement equation \(x[1]+x[2]/2+x[3]/3=1\), the measurement matrix is \(A=[1, 1/2, 1/3]\). Starting at point \(\tilde{x}_0=[0,1,3/2]^T\), by restricted projection it derives \(\tilde{x}_1=[0,2,0]^T\) as shown in Example 3.3.

For the support index set \(S=\{2\}\), to check whether the subgradient condition is satisfied for the vertex \(\tilde{x}_1\) of the feasible set. Notice the gradient \(\text{ sign }(\tilde{x}_1[2])\) restricted to the subspace \(\{[0,\xi ,0], \xi \in R\}\) is 1. To satisfy the condition \(A[:,2]^T\lambda =1\), it follows that \(\lambda =2\). It is clear that \(A[:,1]^T\lambda =2>1\), which means the point \(\tilde{x}_1\) is not the minimal solution. Let \(h=[h_1,h_2,0]^T\) be a possible direction for update. The feasible direction h should belong to the null space of matrix A. Let \(h_1=-1\), it follows \(h_2=2\), and thus \(h=[-1,2,0]^T\). Hence, it derives next iteration \(\tilde{x}_2=\tilde{x}_1-h=[1,0,0]\), which is the minimal solution.

In the above Example 3.4, a feasible search direction is constructed by the information derived from the checking of the subgradient condition. The following refined projection algorithm is developed using the idea of Example 3.4.

We use the notations of step 2 in Algorithm NSP. Suppose that a vertex \(x_t\) of the feasible set F is arrived at t-th iteration, which means \(|S_t|\le m\). To check the subgradient condition, we need firstly to calculate a corresponding coefficient vector \(\lambda \in R^m\) for \(x_t\) and its support index set \(S_t\).

For simplicity of presentation, without loss of generality let us assume that \(S_t=\{1,2,\ldots ,n_1\}\), where \(n_1=|S_t|\). Define a new index set \(S_0\supseteq S_t\) by including \(m-n_1\) new column indices of matrix A to construct a square sub-matrix of A. Without loss of generality, assume that the sub-matrix \(A[:,S_0]\) of A is invertible; otherwise another invertible square sub-matrix with some other new columns may be selected. Thus, the m components of \(\lambda\) can be determined by

$$\begin{aligned} \lambda =(A[:,S_0]^T)^{-1}\text{ sign }(x_t[S_0]), \end{aligned}$$
(24)

where \(x_t[S_0\setminus S_t]=0\), i.e., the components with newly included indices are zeros.

Now we can check the subgradient condition by the derived \(\lambda\) with the calculation \(A^T\lambda\). The requirement of \(A^T_{S_t}\lambda =\text{ sign }(x_t[S_t])\) has been satisfied by (24). If the condition \(\Vert A_{S_t^c}^T\lambda \Vert _{\infty }\le 1\) is also satisfied, then the optimal point of \((P_1)\) is already attained.

Otherwise, we need to construct a feasible direction for next update by using especially the calculated results. Denote \(c=A^T\lambda\). Let \(i_m\in S_0^c\) be the index for the maximal absolute value of c. Obviously, \(|c[i_m]|>1\). For any point \(h\in \mathcal {N}(A)\), we also have

$$\begin{aligned} c^Th=\lambda ^T Ah=0. \end{aligned}$$
(25)

The new feasible direction \(d_t\) should belong to the null space of matrix A to keep the update movement along the set F. We construct a solution h of the system of linear equations \(Ah=0\) by setting

$$\begin{aligned} h[i_m]=-\text{ sign }(c[i_m]). \end{aligned}$$
(26)

The components of h with indices out of the index set \(S_0\cup \{i_m\}\) are set to zeros. The components of h with indices belonging to \(S_0\) is calculated by

$$\begin{aligned} h[S_0]=(A[:,S_0])^{-1}A[:,i_m]\cdot \text{ sign }(c[i_m]). \end{aligned}$$
(27)

Now a vector h of \(\mathcal {N}(A)\) is constructed. It is shown in Lemma 3.2 that the vector \(-h\) constructed is a decreasing direction of \(\Vert x\Vert _1\) at \(x_t\). Finally it is normalized to construct the feasible direction of \(d_t\).

The direction h can be constructed in an advanced version to form an inner path of the feasible set F. Denote \(T\subseteq S_0^c\) the index set satisfying \(|c[j]|>1\) for \(j\in T\). Now construct a solution h of the system of linear equations \(Ah=0\) by letting

$$\begin{aligned} h[T]=-\text{ sign }(c[T]). \end{aligned}$$
(28)

The components of h with indices out of the index set \(S_0\cup T\) are set to be zeros. The components of h with indices belonging to \(S_0\) is calculated by

$$\begin{aligned} h[S_0]=(A[:,S_0])^{-1}\sum _{j\in T}A[:,j]\cdot \text{ sign }(c[j]). \end{aligned}$$
(29)

Now a vector h of \(\mathcal {N}(A)\) is constructed.

Now, we summarize the main steps of the refined projection algorithm below.

Table 2 Subgradient descend algorithm
Full size table

Let us explain more about the updating step of RSD algorithm. First the next search direction \(d_t\) is constructed according to the sub-routine (i) or (ii) by checking whether the number of support index \(S_t\) of \(x_t\) is greater than or less than (equaling) m, which is the number of measurement equations. The construction (i) is the restricted projected gradient at point \(x_t\) and the construction (ii) is developed by checking the subgradient condition. The step (iii) is to implement the update by using the constructed search direction from (i) or (ii). The proposed RSD algorithm can be extended to a more advanced version by including inner path of the feasible set F, rather than an edge path in Table  2.

We further explain the relation between the Naive Subspace Projection Algorithm and the Refined Projection Algorithm. The Naive algorithm may fail to find the genuine sparsest signal, since the search direction by projection of gradient/subgradient may reduce to a zero vector when the genuine sparsest signal is not yet arrived. While, the refined algorithm overcomes this problem by using restricted projection of gradient/subgradient, which can always find the sparsest solution if the condition of Theorem 3.1 holds.

Remark 3.2

An advanced version of RSD algorithm is to modify the step2 (c) in Table  2 to be the following:

(c\(^{\prime }\)) Otherwise, \(|c[i_m]|>1\). Denote \(T\subseteq S_0^c\) the index set satisfying \(|c[j]|>1\) for \(j\in T\). Construct a vector \(h\in \mathcal {N}(A)\). Set h[T] and \(h[S_0]\) by (28) and (29) respectively, and other components be zeros.

3.3 Convergence analysis of the proposed algorithms

There are two key steps of the proposed RSD algorithm. One is the restricted projection and the other is the checking of subgradient condition. Correspondingly, we first analyze the two key steps in details respectively, and then establish a convergence result for the refined projection algorithm.

Let us recall some basic notations and facts here for convenience. We call a point \(\xi \in R^n\) is regular if \(\xi\) has no zero components. It is clear that the gradient of \(\Vert x\Vert _1\) at \(\xi\) is \(d=\text{ sign }(\xi )\). It is well-known that under this case the gradient d is an increasing direction for function \(\Vert x\Vert _1\), meanwhile \(-d\) is a decreasing direction. For a point \(\eta \in R^n\) with some zero components, denote the support index set of \(\eta\) by \(S_{\eta }\). If we restrict the subgradient \(\text{ sign }(\eta )\) of \(\eta\) in the subspace \(\{\zeta \in R^{|S_{\eta }|}|\zeta _i=0, i\in S_{\eta }^c\}\), it follows that the subgradient \(\text{ sign }(\eta )\) can be viewed as the gradient of function \(\Vert \zeta [S_{\eta }]\Vert _1\) at point \(\eta [S_{\eta }]\), in other words, it is a relatively regular point in this restricted subspace. Hence, the projection of \(\text{ sign }(\eta [S_{\eta }])\) to this subspace is still an increasing direction and its reverse is a decreasing direction. This idea is used to establish the following assertion.

We next show the effectiveness of the projection step, i.e., step 2(i) of both Algorithms NSP and RSD. Except the initial step, the projection is restricted to a suitable subspace to derive feasible direction, please refer to Example 3.1 for a counter-example showing that projection without restriction may not be a decreasing direction for the objective function \(\Vert x\Vert _1\). Thus, the subgradient of an irregular point should be cautiously projected to a suitable subspace to derive feasible direction.

Lemma 3.1

Suppose the matrices \(A[:,S_0]\) involved in step 2(i) of Algorithms NSP or RSD are full of row rank. Then, by at most \((n-m)\) iterations of step 2(i)(iii) of either Algorithms NSP or RSD, the objective function \(\Vert x\Vert _1\) of \((P_1)\) is strictly decreasing and the resultant estimate is a vertex of the feasible set F.

Proof

We first point out a fact that if the projection turns to be zero vector at certain step of the algorithm, then a minimal point is arrived. Indeed, by (12),

$$\begin{aligned} Pr(A)\text{ sign }(x_t)=\text{ sign }(x_t)-A^T(AA^T)^{-1}A\text{ sign }(x_t)=0, \end{aligned}$$
(30)

which implies that the condition of Theorem 2.2 is satisfied by \(\lambda =(AA^T)^{-1}A\text{ sign }(x_t)\). Thus, \(x_t\) is a minimal solution of \((P_1)\). Hence, we assume the projectors are not degenerated.

As stated in the beginning of this subsection, for an ordinary gradient \(d\in R^n\) of a continuously differentiable function \(f: R^n\rightarrow R\), the projection of d into a subspace defined by the null space of matrix A is still an increasing direction for function f and its reverse is a decreasing direction. This can be proved by the definition of directional differential of function f.

Without loss of generality, suppose that at the first step \(x_0\) is a regular point, thus the 1-norm value of the derived \(x_1\) is strictly less than that of \(x_0\). By selecting \(x_1\) through (20), it is clear that \(x_1\) has at least one zero component (for simplicity of presentation, let the index of the zero component be n). Note that the first \((n-1)\) components of \(\text{ sign }(x_1)\), subgradient of \(x_1\), becomes the gradient of function \(\big |x[1]\big |+\cdots +\big |x[n-1]\big |\) at point \((x_1[1],\ldots ,x_1[n-1])\) in the subspace \(R^{n-1}\). This means that the projection of \((\text{ sign }(x_1[1]),\ldots ,\text{ sign }(x_1[n-1]))^T\) to linear subspace \(A[:,1:n-1]h[1:n-1]=0\) (i.e., null space of matrix \(A[:,1:n-1]\)) is still an increasing direction and its reverse a decreasing direction in this linear subspace. Thus, the 1-norm value of the derived \(x_2\) is further strictly less than that of \(x_1\). The process continues until a derived point \(x_t\) with equaling or more than \(n-m\) zero components (i.e., a vertex of the feasible set F). Note that the strict decreasing of 1-norm at each step, the assertion follows directly. \(\square\)

The assumption of Lemma 3.1 on the related sub-matrices of A is simply used for the implementation of the algorithm. However, if the related matrices are not full of row rank, the projection may still be able to be implemented by simply deleting some rows of matrix A. This requirement can be satisfied with probability 1 for a randomly generated matrix A, and thus exception extremely rarely occurs.

Next we consider the second step of subgradient condition checking used in the refined projection algorithm.

Lemma 3.2

Suppose the matrices \(A[:,S_0]\) used in step 2(ii) of Algorithm RSD are invertible. Then, the vector \(-h\) constructed in step 2(ii) of Algorithm RSD is a decreasing direction of \(\Vert x\Vert _1\) at \(x_t\).

Proof

The support index set of h is \(S_0\cup \{i_m\}\). For simplicity of presentation, without loss of generality, let \(S_t=\{1,2,\ldots ,n_1\}\) and \(S_0=\{1,2,\ldots ,m\}\), where \(n_1=|S_t|\).

Recall the definition of \(\lambda\) by (24), it is clear that \(c[n_1+1:m]=0\). Thus, by (25) it follows that

$$\begin{aligned} c[1]h[1]+\cdots +c[n_1]h[n_1]+c[i_m]h[i_m]=0. \end{aligned}$$
(31)

Now we consider sufficient small \(\varepsilon >0\) such that \(\text{ sign }(x_t[i])=\text{ sign }(x_t[i]-\varepsilon h[i])\) with \(i=1,\ldots ,n_1\). In other words, the submission by \(\varepsilon h\) is sufficient small to keep the sign of each component of \(x_t[S_t]\). Under this setting, it is clear that

$$\begin{aligned} \big |x_t[i]-\varepsilon h[i]\big |=\text{ sign }(x_t[i])(x_t[i]-\varepsilon h[i]) \end{aligned}$$
(32)

for \(i=1,\ldots ,n_1\). By (31) and (32), it follows

$$\begin{aligned} \Vert x_t-\varepsilon h\Vert _1&=\sum _{i\in S_t}\text{ sign }(x_t[i])(x_t[i]-\varepsilon h[i])+\varepsilon \nonumber \\&=\Vert x_t\Vert _1-\varepsilon \sum _{i\in S_t}\text{ sign }(x_t[i])h[i]+\varepsilon \nonumber \\&=\Vert x_t\Vert _1-\varepsilon (c^Th-c[i_m]h[i_m])+\varepsilon \nonumber \\&=\Vert x_t\Vert _1-\varepsilon \big |c[i_m]\big |+\varepsilon \nonumber \\&=\Vert x_t\Vert _1-\varepsilon (\big |c[i_m]\big |-1)<\Vert x_t\Vert _1, \end{aligned}$$
(33)

where formula (24) and fact that \(c=A^T\lambda\) is used in the third step, in the last step we use the fact that \(|c[i_m]|>1\). Therefore, the vector \(-h\) is a decreasing direction of \(\Vert x\Vert _1\) at \(x_t\). \(\square\)

The result of Lemma 3.2 can be proved in another way by showing that the vector h is an increasing direction of \(\Vert x\Vert _1\) at \(x_t\). Define \(g[S_0]=c[S_0]\), \(g[i_m]=\text{ sign }(c[i_m])\), and other components of g are all zeros. By (6), it is clear that the vector g is a subgradient of \(\Vert x\Vert _1\) at \(x_t\). By definition of subgradient,

$$\begin{aligned} \Vert x_t+h\Vert _1-\Vert x_t\Vert _1&\ge g^Th=g[1]h[1]+\cdots +g[n_1]h[n_1]\\&\quad +g[i_m]h[i_m]\\&=(c[1]h[1]+\cdots +c[n_1]h[n_1]+c[i_m]h[i_m])\\&\quad +(g[i_m]-c[i_m])h[i_m]\\&=(g[i_m]-c[i_m])h[i_m]\\&=(g[i_m]-c[i_m])(-\text{ sign }(c[i_m]))\\&=|c[i_m]|-1>0, \end{aligned}$$

which implies the direction h is an increasing direction for \(\Vert x\Vert _1\) at \(x_t\). Hence, the constructed direction h for \(\Vert x\Vert _1\) serves as ordinary gradient direction. The direction h constructed by the advanced version of RSD algorithm presented in Remark 3.2 can similarly been proved to be an increasing direction of \(\Vert x\Vert _1\) at \(x_t\).

Now we can conclude the convergence of the refined projection algorithm.

Theorem 3.1

Suppose that any \(m\times m\) sub-matrix of \(A\in R^{m\times n}\) is invertible, where \(m<n\). Then, by the refined projection algorithm RSD, a minimal solution of \((P_1)\) is derived in finite iterations.

Proof

We firstly assume that the projector in each step is not degenerated. Otherwise, as shown in the proof of Lemma 3.1, a minimal of \((P_1)\) is achieved.

By Lemma 3.1, it is clear that after the first at most \(n-m\) iterations, a vertex \(x_t\) of set F is attained and the objective function \(\Vert x\Vert _1\) is strictly decreased.

Now Algorithm RSD goes to the step 2(ii) case, if the subgradient condition of Theorem 2.2 is satisfied, a minimal point of \((P_1)\) is achieved. Otherwise, the estimation moves to another vertex of the feasible set F and the objective function \(\Vert x\Vert _1\) is further strictly decreased. Since the number of vertices of the set F belonging to \(B(x_0,r)\) is finite, the algorithm ends in a finite number of iterations and arrives at a minimal solution of \((P_1)\). \(\square\)

The nonsingluar assumption of sub-matrices of matrix A is used to simplify the presentation, which can be reduced to that the derived submatrices occurred in the algorithm are invertible. For a randomly generated matrix A, the required condition is satisfied with probability 1. The convergence to optimal solution of the advanced version of RSD algorithm presented in Remark 3.2 can also been similarly proved.

By the design of the refined projection algorithm, it is clear that the relaxed subgradient condition stated in Theorem 2.2 can be guaranteed, thus a solution of \((P_1)\) can be asserted. Moreover, once the minimal solution of \((P_1)\) is unique, i.e., if the subgradient condition is satisfied, the unique sparsest solution can be attained by the refined projection algorithm.

Corollary 3.1

Under the subgradient condition of Theorem 2.1, by the refined projection algorithm RSD, the unique solution of \((P_1)\) is attained.

4 Construction of matrix satisfying subgradient condition

Subgradient condition is a minimal, sufficient and necessary requirement for successful 1-norm sparse signal learning. An important problem is how to detect whether a matrix satisfies the subgradient condition or not, which is generally difficult to answer completely. On the contrary, in this section we develop construction method of measurement matrix to guarantee the subgradient condition of Theorem 2.1. This result shows possible way to find a general method to check the subgradient condition. Besides, this construction method is also implemented in the numerical simulation for tests.

Denote the maximum column sum matrix norm [48] by \(\Vert M\Vert _1\) for a matrix M, i.e.,

$$\begin{aligned} \Vert M\Vert _1=\max _{j}\sum _{i}|M_{ij}|. \end{aligned}$$

Theorem 4.1

Set \(k<m<n\). Suppose a matrix \(A\in R^{m\times n}\), by certain row operation \(Q_r\in R^{m\times m}\) and possible column permutation \(Q_c\in R^{n\times n}\), turns to be the following form:

$$\begin{aligned} \bar{A}=Q_rAQ_c=\begin{bmatrix} I_k \quad B_{k\times (n-k)} \\ C_{(m-k)\times n} \\ \end{bmatrix}_{m\times n}, \end{aligned}$$

where the maximum column sum matrix norm of the sub-matrix B is less than 1, i.e., \(\Vert B\Vert _1<1\), and the matrix C is an arbitrary sub-matrix of suitable size. Then the matrix A satisfies the subgradient condition of Theorem 2.1.

Proof

Denote \(b_{ij}\) be the (i, j)-th entry of matrix B. The condition \(\Vert B\Vert _1<1\) means that \(\sum _{i=1}^k|b_{ij}|<1\) for any \(j=1,\ldots ,n-k\).

For any given \(\bar{x}\) with its support index set \(\bar{S}=\{1,2,\ldots ,k\}\), let

$$\begin{aligned} \bar{\lambda }=[\text{ sign }(x_1),\ldots ,\text{ sign }(x_k),0,\ldots ,0]^T. \end{aligned}$$
(34)

It is clear that the subgradient condition is satisfied for matrix \(\bar{A}\) with respect to \(\bar{x}\), since \(\bar{A}_{\bar{S}}^T\bar{\lambda }=\text{ sign }(\bar{x}_{\bar{S}})\) and \(\Vert \bar{\lambda }^T\bar{A}_{\bar{S}^c}\Vert _{\infty }<1\).

Denote \(\lambda =Q_r^{-1}\bar{\lambda }\) and S the inverse image of \(\bar{S}\) under the permutation operation \(Q_c\). It is clear that the similar formulae for \(\lambda\) and S holds for matrix A. This completes the proof. \(\square\)

It is worth pointing out that the support index set of matrix A and \(\bar{A}\) may be different when checking the subgradient condition.

Based on Theorem 4.1, to construct measurement matrix for given parameters \(k<m<n\) and support index set S, a typical construction algorithm is presented as follows.

Table 3 Construction of matrix satisfying subgradient condition
Full size table

5 Simulation

In this section, we compared the proposed RSD algorithm with some other state-of-the-art algorithms: FISTA [25], AP (alternating projection method) [30], IPP (Iterative Proximal Projection) [34], SEF (Shannon entropy function) [32] in the literature. Next we consider the signal recovery rate with noiseless observation case and estimation bias with noise observation case, respectively.

1). Comparison of recovery biases and time with designed measurement matrices.

It is proved by Theorem 3.1 that under the ideal observation model, i.e., the noiseless case model (1), the RSD algorithm can exactly learn and recover the sparse signal if the subgradient condition holds.

Let sparsity \(k=1,\ldots ,10\). For each k, set \(m=2k\), \(n=5m+2=10k+2\), the simulation generates a \(m\times n\) measurement matrix A by the construction method presented in Sect. 4 to guarantee the subgradient condition. The k-sparse source signal x was also randomly generated with its support components being integers belonging to the interval \([-10,10]\). The support locations and their signs were all randomly assigned. Based on the observation \(y=Ax\), the algorithms: RSD, FISTA, IPP, AP, SEF, were tested, and their average recovery biases were calculated over \(N=100\) tests for each k. The recovery bias for a single test is calculated by \(\Vert x_e-x_0\Vert _2/\Vert x_0\Vert _0\), where \(x_0\) is the real solution and \(x_e\) is the recovery solution by various algorithms (Fig. 2). The logarithm (with base 10) average signal recovery rates and logarithm (with base 10) operation times for these methods were plotted in Fig. 3, respectively. It is shown that the logarithm recovery biases of RSD algorithm is the smallest among all these algorithms. The small quantity of the bias of RSD around \(10^{-10}\) indicates that the recovery rate is 100%, which is caused by the fact that the measurement matrices all satisfy the subgradient condition of Theorem 2.1, since the measurement matrices were all generated by the algorithm described in Table  3 of Sect. 4. This construction implies that the source sparse signal is the unique minimal 1-norm solution, which can be successfully learned by RSD algorithm as shown in Theorem 3.1. The logarithm average operation time of RSD also highlights the potential ability of this algorithm.

Under the same setting of the above description except that the observation \(y=Ax+v\), where each element of v obeying \(\mathcal {N}(0,0.01^2)\), the logrithm recovery biases and logarithm operation times of these algorithms were plotted in Fig. 4, respectively. The recovery biases of RSD algorithm are still almost the best.

2). Comparison of recovery biases and time with random measurement matrices.

At each sparsity \(k=1,\ldots ,10\), the average estimation biases for the algorithms: RSD, FISTA, IPP, AP, SEF, were calculated over \(N=100\) sample paths. The other settings are similar to the above noiseless setting of case (1). Let \(m=2k\) and \(n=2m+2=4k+2\). Let each element of the measurement matrix \(A\in R^{m\times n}\) be randomly generated with Gaussian distribution \(\mathcal {N}(0,1/m)\). The logarithm (with base 10) average estimation biases and logarithm operation times for these algorithms were plotted in Fig. 5, respectively. It is clear that the biases of the proposed RSD algorithm are almost the minimal, and FISTA and IPP performs next, and AP and ESF are the worst. The logarithm average operation time of RSD is quite comparative among other algorithms.

Let the measurement matrices be randomly generated as above, e.g., each element of the measurement matrix obeying \(\mathcal {N}(0,1/m)\). Let the observation model be \(y=Ax+v\), where the each component of the noise v was randomly generated by Gaussian distribution \(\mathcal {N}(0,0.01^2)\). The logarithm (with base 10) average estimation biases and logarithm operation times of these algorithms were respectively plotted in Fig. 6. The proposed RSD algorithm still outperforms other algorithms. The performance order of other algorithms from best to worst is similar to the above case. Meanwhile, the logarithm average operation time of RSD is still comparative among other algorithms.

3). Comparison of image reconstruction.

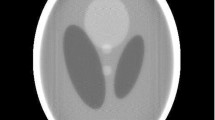
In this subsection, 6 standard gray images with the size of \(256\times 256\) were used for image reconstruction experiment. Each image was divided into small \(32\times 32\) blocks first. And thus each block was transformed by 5-layer wavelet transformation to approximate a sparse signal by using the Haar wavelet. Denote a \(32\times 32\) block by B and the 5-layer wavelet 1-dimensional transformation matrix by W, then the block was transformed to \(X=WBW'\), whose columns are all near sparse signals. Generate a random observation matrix M by letting each element obeying a standard Gaussian distribution. The observation was then obtained by \(Y=MX\). Each column X( : , i) of X can be recovered by using the proposed algorithm and the comparison algorithms using the observation Y( : , i) and measurement matrix M. Denote the total reconstructed signal by \(\hat{X}\). Hence, the reconstructed image block was obtained by \(\hat{B}=W'\hat{X}W\).

The comparison of image reconstruction by the proposed algorithm and the state-of-the-art algorithms are shown in Figs. 7, 8, 9, 10, 11 and 12, where total 6 images were tested. It is clear that the proposed RSD algorithm outperforms the other algorithms in PSNR. Here \(\text{ PSNR }=10log_{10}(255^2/\text{MSE})\), where \(\text{ MSE }\) is total estimation error.

4). Experimental analysis

From the sparse signal learning and recovery experiments as shown in Figs. 3, 4, 5 and 6, we learn that the proposed restricted subgradient descend method is more competitive than the state-of-the-art methods including FISTA, IPP, AP and SEF in signal recovery accuracy. The major reason is that these methods are the approximate computation methods for sparse signal learning. Specifically, FISTA introduces extra quadratic term to the objective function to relax the \(l_1\) optimization problem, which leads to inexact sparse signal estimation results. As for AP, the hard threshold operator used in the optimization framework makes it hard to generate good signal recovery rate. SEF adopts a refined multiple proximal gradient method for signal recovery. However, the entropy function used in SEF is not a convex function, that makes the performance of SEF highly depend on the initial point. Similarly, IPP is also an approximation method, which cannot achieve exact sparse signal learning and recovery.

Unlike the above-mentioned methods, we used a restricted subgradient learning scheme for optimization. Based on our observations as mentioned above, an irregular point can be viewed as a regular point in a restricted subspace. Therefore, the restricted subgradient in suitable subspace can act as common case to derive decreasing search direction. The proposed subgradient condition checking-based method is an inner path (rather than an edge) of the feasible simplex, and thus the updated point after pivoting can be a border point (rather than a vertex) of the feasible simplex. The deceasing direction of \(l_1\) objective function can be easily constructed by the restricted projection of the subgradient to the subspace spanning by restriction equations, for an irregular point with the number of its nonzero components larger than the number of restriction equations. With these reasons, the proposed RSD algorithm can lean more exact sparse signals compared with the state-of-the-art methods. Such an effectiveness is also validated by a visualized image reconstruction experiment as shown in Figs. 7, 8, 9, 10, 11 and 12.

Moreover, we also developed Theorem 3.1 to guarantee the convergence of the refined projection algorithm. The logarithm operation times shown in Figs. 3, 8, 9 and 6 demonstrate that RSD can achieve satisfactory performance in efficiency among all the comparison methods.

Fig. 3
figure 3

The measurement matrix is generated by algorithm described in Table  3 and the observation is noiseless. a The plot of logarithm average recovery biases v.s. sparsity by algorithms: RSD, FISTA, IPP, AP, SEF. b The plot of logarithm average operation times v.s. sparsity by these algorithms

Full size image
Fig. 4
figure 4

The measurement matrix is generated by algorithm described in Table  3 and the observation is disturbed by noise. a The plot of logarithm average recovery biases v.s. sparsity by algorithms: RSD, FISTA, IPP, AP, SEF. b The plot of logarithm average operation times v.s. sparsity by these algorithms

Full size image
Fig. 5
figure 5

The measurement matrix is randomly generated and the observation is noiseless. a The plot of logarithm average recovery biases v.s. sparsity by algorithms: RSD, FISTA, IPP, AP, SEF. b The plot of logarithm average operation times v.s. sparsity by these algorithms

Full size image
Fig. 6
figure 6

The measurement matrix is randomly generated and the observation is disturbed by noise. a The plot of logarithm average recovery biases v.s. sparsity by algorithms: RSD, FISTA, IPP, AP, SEF. b The plot of logarithm average operation times v.s. sparsity by these algorithms

Full size image
Fig. 7
figure 7

Comparison of image reconstruction by algorithms. a original image; b by RSD, PSNR = 41.3892; c by FISTA, PSNR = 18.2492; d by IPP, PSNR = 18.3036; e by AP, PSNR = 35.8963; f by SEF, PSNR = 17.9667

Full size image
Fig. 8
figure 8

Comparison of image reconstruction by algorithms. a Original image; b by RSD, PSNR = 37.1395; c by FISTA, PSNR = 15.3421; d by IPP, PSNR = 15.3717; e by AP, PSNR = 30.7165; f by SEF, PSNR = 15.1375

Full size image
Fig. 9
figure 9

Comparison of image reconstruction by algorithms. a Original image; b by RSD, PSNR = 41.9982; c by FISTA, PSNR = 18.0196; d by IPP, PSNR = 18.0827; e by AP, PSNR = 36.5923; f by SEF, PSNR = 17.7589

Full size image
Fig. 10
figure 10

Comparison of image reconstruction by algorithms. a original image; b by RSD, PSNR = 38.5720; c by FISTA, PSNR = 18.6456; d by IPP, PSNR = 18.6509; e by AP, PSNR = 32.9794; f by SEF, PSNR = 18.3231

Full size image
Fig. 11
figure 11

Comparison of image reconstruction by algorithms. a original image; b by RSD, PSNR = 40.7556; c by FISTA, PSNR = 18.0117; d by IPP, PSNR = 18.0277; e by AP, PSNR = 35.1457; f by SEF, PSNR = 17.6824

Full size image
Fig. 12
figure 12

Comparison of image reconstruction by algorithms. a original image; b by RSD, PSNR = 40.9285; c by FISTA, PSNR = 16.8940; d by IPP, PSNR = 16.9366; e by AP, PSNR = 33.8665; f by SEF, PSNR = 16.6582

Full size image

6 Conclusion

An effective subgradient descend based learning algorithms are developed for sparse signal learning. Not like the approximate methods, e.g., FISTA, IPP, AP, SEF algorithms, the proposed refined RSD algorithm can derive an exact optimal solution of the SSL optimization issue \((P_1)\) (objective function is \(\Vert x\Vert _1\)). Moreover, if the optimal solution of \((P_1)\) is unique, the RSD algorithm approach the unique optimum within finite iterative steps. A naive projection algorithm is firstly proposed by using purely restricted projection. Then a refined projection algorithm extends the naive version by including a step of subgradient condition checking. Under the most minimal subgradient condition for 1-norm sparse signal learning issue, the refined RSD projection algorithm can successfully learn the unique minimal solution of \((P_1)\). Demonstration simulations were implemented to verify 100% success for measurement matrix satisfying the subgradient condition. The operation time is also very competitive among the other state-of-the-art sparse signal learning algorithms in the literature.