Availability and profit analysis of a feeding system in sugar industry

Abstract

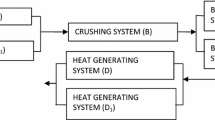
This paper discusses a feeding system of the sugar industry consisting of six subsystems—unloaders, cane carrier and cutter unit, crushing unit, boiler unit, bagasse carrier unit and turbines. Cane carrier and cutter unit, crushing unit, bagasse carrier unit and boiler unit are working in series. In sub-system ‘unloaders’ one unloader is operative and another is kept as cold standby whereas, in sub-system ‘turbines’ both the turbines work in parallel. The distribution of failure times of sub-systems of feeding system is taken as exponential while the distribution of repair times of sub-systems is considered as arbitrary. The feeding system is analyzed by using supplementary variable technique. A particular case is also considered to show the behavior of availability and profit of the feeding system.

Appendices

Appendix 1

1.1 Solution of partial differential Eqs. (1–31) by Lagrange’s Method

For illustration let us consider Eq. (31):

$$\left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \beta_{1} (x)} \right]p_{34} (x,t) = \alpha_{1} p_{4} (t)$$

Initial and boundary conditions for this equation are

$$p_{0} (0) = 1,\quad p_{34} (x,0) = 0,\quad p_{34} (0,t) = \alpha_{1} p_{4} (t)$$

This is first order linear partial differential equation (Lagrange’s type) and can be solved using initial and boundary conditions:

The subsidiary equation for (31) is:

$$\frac{dx}{1} = \frac{dt}{1} = \frac{{dp_{34} (x,t)}}{{ - \beta_{1} (x)p_{34} (x,t) + \alpha_{1} p_{4} (t)}}$$

Solution of this equation is $p_{34} (x,t) = \phi_{34} (t - x) + \alpha_{1} p_{4} (t)e^{{ - \int\limits_{0}^{\infty } {\beta_{1} (x)dx} }} \left\{ {1 + \int\limits_{0}^{\infty } {e^{{\int\limits_{0}^{\infty } {\beta_{1} (x)dx} }} dx} } \right\}$

Similarly we can solve other Eqs. (1)–(30) by using same approach.

Appendix 2

2.1 Supplementary variable technique

When the repair rate or failure rate or both are time-dependent, the system loses its Markovian character, In this situation, the future event will not depend on present only (like Markov events) but will depend past also. These events are known as non-Markovian events.

As this paper discusses a feeding system of the sugar industry consisting of six subsystems—unloaders, cane carrier and cutter unit, crushing unit, boiler unit, bagasse carrier unit and turbines, with constant failure rates and arbitrary repair rates. Now the system is of non-Markovian nature.

By introducing a new variable, called supplementary variable, the non-Markovian nature of the system is changed to Markovian.

Here we introduced variable x (as a supplementary variable) now the nature of the system becomes Markovian, e.g. the equation number 1(having x as a supplementary variable):

$$\begin{aligned} p_{0} (t + \Delta t) & = [1 - \alpha_{1} \Delta t - \alpha_{2} \Delta t - \alpha_{3} \Delta t - \alpha_{4} \Delta t - \alpha_{5} \Delta t - \alpha_{6} \Delta t - \alpha_{7} \Delta t]p_{0} (t) + \int\limits_{0}^{\infty } {\beta_{1} (x)p_{1} (x,t)dx\Delta t} \\ & \quad + \int\limits_{0}^{\infty } {\beta_{2} (x)p_{8} (x,t)dx\Delta t + \int\limits_{0}^{\infty } {\beta_{3} (x)p_{9} (x,t)dx\Delta t} + \int\limits_{0}^{\infty } {\beta_{4} (x)p_{10} (x,t)dx\Delta t} + } \int\limits_{0}^{\infty } {\beta_{5} (x)p_{11} (x,t)dx\Delta t} + \int\limits_{0}^{\infty } {\beta_{6} (x)p_{3} (x,t)dx\Delta t} + \int\limits_{0}^{\infty } {\beta_{7} (x)p_{2} (x,t)dx\Delta t} \\ \end{aligned}$$

Dividing both sides by ∆t

$$\begin{aligned} \frac{{p_{0} (t + \Delta t) - p_{0} (t)}}{\Delta t} & = [ - \alpha_{1} - \alpha_{2} - \alpha_{3} - \alpha_{4} - \alpha_{5} - \alpha_{6} - \alpha_{7} ]p_{0} (t) + \int\limits_{0}^{\infty } {\beta_{1} (x)p_{1} (x,t)dx} + \int\limits_{0}^{\infty } {\beta_{2} (x)p_{8} (x,t)dx} \\ & \quad + \int\limits_{0}^{\infty } {\beta_{3} (x)p_{9} (x,t)dx} + \int\limits_{0}^{\infty } {\beta_{4} (x)p_{10} (x,t)dx} + \int\limits_{0}^{\infty } {\beta_{5} (x)p_{11} (x,t)dx} + \int\limits_{0}^{\infty } {\beta_{6} (x)p_{3} (x,t)dx} + \int\limits_{0}^{\infty } {\beta_{7} (x)p_{2} (x,t)dx} \\ \end{aligned}$$

$$\begin{aligned} \left[ {\frac{{dp_{0} (t)}}{dt}} \right] + [\alpha + \alpha_{2} + \alpha_{3} + \alpha_{4} + \alpha_{5} + \alpha_{6} + \alpha_{7} ]p_{0} (t) = \int\limits_{0}^{\infty } {\beta_{1} (x)p_{1} (x,t)dx} + \int\limits_{0}^{\infty } {\beta_{2} (x)p_{8} (x,t)dx} \hfill \\ + \int\limits_{0}^{\infty } {\beta_{3} (x)p_{9} (x,t)dx} + \int\limits_{0}^{\infty } {\beta_{4} (x)p_{10} (x,t)dx} + \int\limits_{0}^{\infty } {\beta_{5} (x)p_{11} (x,t)dx} + \int\limits_{0}^{\infty } {\beta_{6} (x)p_{3} (x,t)dx} + \int\limits_{0}^{\infty } {\beta_{7} (x)p_{2} (x,t)dx} \hfill \\ \end{aligned}$$

In this way, with the help of supplementary variable technique we can obtain various differential difference Eqs. (1–31) and that are solved by using Lagrange’s method as explained in Appendix 1.