1 Introduction

Memristor, the missing fourth passive circuit element, is a nano-scale circuit element originally postulated by Chua [1] and realized by a team led by Stanley William from the Hewlett-Packard Company [2]. Recently, research on circuit based on memristor is becoming a focal topic for research because it will reduce power consumption to use memristors in computer by saving the time to reload data and could lead to the human-like learning. Memristor, a thin semiconductor film between two metal contacts with variable resistance which changes automatically as its voltage changing, can be used as a tunable parameter in control systems [2]. Nowadays, memristor-based systems have been applied in many practical fields such as lag synchronization of memristive neural networks application in pseudo-random generators [3], image encryptions by lag synchronization of switched neural networks [4], global exponential stabilization of memristive neural networks and neuromorphic circuits design [5], and dynamic behaviors of memristor-based delayed recurrent networks analysis [6].

The memristor is a passive two-terminal electronic device between the device terminal voltage v(t) and terminal current i(t) [2, 7–9] as shown in Fig. 1, defined as \(v(t) = M(q(t))i(t)\) or \(i(t) = W(\varphi (t))v(t)\), where the nonlinear functions \(M(q)\) and \(W(\varphi )\) are called memristance and memductance, respectively. In the Chua’s circuit case as shown in Fig. 3, the nonlinear resistor is replaced by a flux-controlled memristor whose constitutive relation is described in Fig. 2 and can be expressed as

Fig. 1
figure 1

Charge-controlled memristor (left) and flux-controlled memristor (right)

Full size image
Fig. 2
figure 2

The constitutive relation of the flux-controlled memristor

Full size image
$$q(\varphi ) = b\varphi + 0.5(a - b)(\left| {\varphi + 1} \right| - \left| {\varphi - 1} \right|),$$
(1)

where \(a,\,b > 0\). Therefore, the memductance can be obtained from the \(q(\varphi )\) as

$$W(\varphi ) = \frac{{{\text{d}}q(\varphi )}}{{{\text{d}}\varphi }} = \left\{\begin{array}{ll} a, & | \varphi | <; 1 \\ b, & | \varphi | > 1 \end{array} \right. .$$
(2)

Time delay which is a source of instability, chaos, and oscillation is frequently encountered in linear or nonlinear systems such as communication circuits, teleoperation systems, electronic circuits, chemical processes, biosystems, and so forth [10–12]. Many applicable researches have been done in time-delay chaotic system, since chaos in time-delay system developed by Mackey and Glass [13]. As it is difficult to achieve satisfactory performance with time-delay systems, the stability issue of time-delay systems is practically important in many real-world physical systems.

Owing to its practical applications in many different engineering fields, chaotic synchronization proposed by Pecora and Carroll [14] between drive and response systems has aroused much attraction. Many approaches have been explored for chaotic systems synchronization, for instance, adaptive control, sliding mode control, backstepping design, active control [15–17] and exponential Synchronization for Fractional-Order Chaotic Systems [18]. Based on the universal approximation theorem, fuzzy systems have supplanted conventional technologies in many scientific applications and engineering systems such as Takagi–Sugeno fuzzy systems H∞ control [19] and stability and stabilization criteria for fuzzy neural networks [20]. The fuzzy modeling and synchronization of different memristor-based chaotic circuits is presented in [21]. In this paper, a Takagi–Sugeno (T–S) fuzzy is constructed to approximate a time delay memristor-based Chua’s circuit. Moreover, the fuzzy control vector will be designed to synchronize two different time delay memristor-based Chua’s circuits and the secure communication applications are provided based on the proposed chaotic synchronization structure.

The rest of this paper is organized as follows. In Sect. 2, T–S fuzzy modeling of time delay memristor-based Chua’s circuit is introduced. Fuzzy synchronization issue will be discussed in Sect. 3. Simulation examples are given in Sect. 4. Finally, the conclusion of the paper is drawn in Sect. 5.

2 T-S fuzzy Modeling of Time Delay Memristor-Based Chua’s Circuits

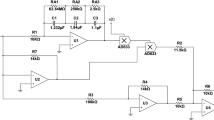
Some memristor-based Chua’s circuits have been proposed by replacing the nonlinear resistor by a memristor and investigated [9, 22]. A time delay memristor-based Chua’s circuit is introduced as shown in Fig. 3 [23] to design a signal generator to produce chaotic behavior by adding a small-amplitude voltage time-delay feedback in the memristor-based Chua’s circuit.

Fig. 3
figure 3

Time delay memristor-based Chua’s circuit

Full size image

The dynamic of the time delay memristor-based Chua’s circuit with a flux-controlled memristor is given by the following set of differential equations:

$$\left\{ \begin{aligned} & \dot{v}_{1} \left( t \right) = \left( { - \frac{1}{{RC_{1} }} - \frac{{W\left( {\varphi \left( t \right)} \right)}}{{C_{1} }}} \right)v_{1} \left( t \right) + \frac{1}{{RC_{1} }}v_{2} \left( t \right) \\ & \dot{v}_{2} \left( t \right) = \frac{1}{{RC_{2} }}v_{1} \left( t \right) - \frac{1}{{RC_{2} }}v_{2} \left( t \right) + \frac{1}{{C_{2} }}i\left( t \right) \\ & \dot{i}\left( t \right) = - \frac{1}{L}v_{2} \left( t \right) - \frac{r}{L}i\left( t \right) - \frac{\varepsilon }{L}\sin \left( {\sigma v_{1} \left( {t - \tau } \right)} \right) \\ & \dot{\varphi }\left( t \right) = v_{1} \left( t \right) \\ \end{aligned} \right.,$$
(3)

where functions \(q(\varphi )\) and \(W(\varphi )\) are described in (1) and (2), respectively. If the following variables and parameter are defined as \(x_{1} = v_{1}\), \(x_{2} = v_{2}\), \(x_{3} = i\), \(x_{4} = \varphi\), \(\frac{1}{{RC_{1} }} = \alpha_{1}\), \(\frac{1}{{C_{1} }} = \alpha_{2}\), \(\frac{1}{{RC_{2} }} = \alpha_{3}\), \(\frac{1}{{C_{2} }} = \alpha_{4}\), \(\frac{1}{L} = \alpha_{5}\), \(\frac{r}{L} = \alpha_{6}\), \(\frac{\varepsilon }{L} = \alpha_{7}\), the (3) can be rewritten as the following form.

$$\left\{ \begin{aligned} & \dot{x}_{1} \left( t \right) = \left( { - \alpha_{1} - \alpha_{2} W\left( {x_{4} \left( t \right)} \right)} \right)x_{1} \left( t \right) + \alpha_{1} x_{2} \left( t \right) \\ & \dot{x}_{2} \left( t \right) = \alpha_{3} x_{1} \left( t \right) - \alpha_{3} x_{2} \left( t \right) + \alpha_{4} x_{3} \left( t \right) \\ & \dot{x}_{3} \left( t \right) = - \alpha_{5} x_{2} \left( t \right) - \alpha_{6} x_{3} \left( t \right) - \alpha_{7} \sin \left( {\sigma x_{1} \left( {t - \tau } \right)} \right) \\ & \dot{x}_{4} \left( t \right) = x_{1} \left( t \right) \\ \end{aligned} \right.,$$
(4)

where the piecewise linear function \(W(x_{4} )\) is given by

$$W\left( {x_{4} } \right) = \left\{ \begin{aligned} &a, \, \left| {x_{4} } \right| \le 1 \hfill \\ &b, \, \left| {x_{4} } \right| > 1 \hfill \\ \end{aligned} \right.$$
(5)

\(C_{1} = 0.1\), \(C_{2} = 1\), \(L = \frac{1}{18}\), \(r = \frac{1}{45}\), \(R = 1\), \(a = 0.3\), \(b = 0.8\), \(\varepsilon = 3\), \(\sigma = 5\), \(\tau = 0.1\). Using Wolf’s method [24, 25] to calculate Lyapunov exponents, the results are \((0.2267,\) \(- 0.0017, - 0.1620, - 3.5196)\), from which we can obviously see that the system is in chaotic state. The 2D projections and 3D phase portraits of the chaotic attractor under the initial condition (0.1, 0.1, 0.1, 0.1) are as shown in Fig. 4.

Fig. 4
figure 4

The 2D projections and 3D phase portraits of the chaotic attractor

Full size image

According to [21], the T–S fuzzy model for time delay memristor-based Chua’s circuit (4) consists of a collection of fuzzy IF–THEN rules as follows:

For \(\dot{x}_{1} \left( t \right) = \left( { - \alpha_{1} - \alpha_{2} W\left( {x_{4} \left( t \right)} \right)} \right)x_{1} \left( t \right) + \alpha_{1} x_{2} \left( t \right)\):Rule 1: IF \(\left| {x_{4} } \right| \le 1\) THEN

$$\dot{x}_{1} \left( t \right) = \left( { - \alpha_{1} - \alpha_{2} a} \right)x_{1} \left( t \right) + \alpha_{1} x_{2} \left( t \right).$$
(6)

Rule 2: IF \(\left| {x_{4} } \right| > 1\) THEN

$$\dot{x}_{1} \left( t \right) = \left( { - \alpha_{1} - \alpha_{2} b} \right)x_{1} \left( t \right) + \alpha_{1} x_{2} \left( t \right).$$
(7)

If \(M_{1}\) and \(\, M_{2}\) are defined as

$$M_{1} = \left\{ \begin{aligned} & 1,\quad \left| {x_{4} \left( t \right)} \right| \le 1 \\ & 0,\quad \left| {x_{4} \left( t \right)} \right| > 1 \\ \end{aligned} \right., \, \quad \, M_{2} = \left\{ \begin{aligned} & 0,\quad \left| {x_{4} \left( t \right)} \right| \le 1 \\ & 1,\quad \left| {x_{4} \left( t \right)} \right| > 1 \\ \end{aligned} \right.,$$
(8)

the simplified two nonlinear subsystems can be obtained. The first nonlinear subsystem under fuzzy rule 1 is described as follows:

$$\left\{ \begin{aligned} & \dot{x}_{1} \left( t \right) = \left( { - \alpha_{1} - \alpha_{2} a} \right)x_{1} \left( t \right) + \alpha_{1} x_{2} \left( t \right) \\ & \dot{x}_{2} \left( t \right) = \alpha_{3} x_{1} \left( t \right) - \alpha_{3} x_{2} \left( t \right) + \alpha_{4} x_{3} \left( t \right) \\ & \dot{x}_{3} \left( t \right) = - \alpha_{5} x_{2} \left( t \right) - \alpha_{6} x_{3} \left( t \right) - \alpha_{7} \sin \left( {\sigma x_{1} \left( {t - \tau } \right)} \right) \\ & \dot{x}_{4} \left( t \right) = x_{1} \left( t \right) \\ \end{aligned} \right..$$
(9)

The state-space representation of (9) is given as

$$\left[ {\begin{array}{*{20}c} {\dot{x}_{1} } \\ {\dot{x}_{2} } \\ {\dot{x}_{3} } \\ {\dot{x}_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \alpha_{1} - \alpha_{2} a} & {\alpha_{1} } & 0 & 0 \\ {\alpha_{3} } & { - \alpha_{3} } & {\alpha_{4} } & 0 \\ 0 & { - \alpha_{5} } & { - \alpha_{6} } & 0 \\ 1 & 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ {x_{4} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { - \alpha_{7} } \\ 0 \\ \end{array} } \right]\sin \left( {\sigma x_{1} \left( {t - \tau } \right)} \right).$$
(10)

In the same way, the second nonlinear subsystem under fuzzy rule 2 is described as follows:

$$\left\{ \begin{aligned} & \dot{x}_{1} \left( t \right) = \left( { - \alpha_{1} - \alpha_{2} b} \right)x_{1} \left( t \right) + \alpha_{1} x_{2} \left( t \right) \\ & \dot{x}_{2} \left( t \right) = \alpha_{3} x_{1} \left( t \right) - \alpha_{3} x_{2} \left( t \right) + \alpha_{4} x_{3} \left( t \right) \\ & \dot{x}_{3} \left( t \right) = - \alpha_{5} x_{2} \left( t \right) - \alpha_{6} x_{3} \left( t \right) - \alpha_{7} \sin \left( {\sigma x_{1} \left( {t - \tau } \right)} \right) \\ & \dot{x}_{4} \left( t \right) = x_{1} \left( t \right) \\ \end{aligned} \right..$$
(11)

The state-space representation of (11) is given as

$$\left[ {\begin{array}{*{20}c} {\dot{x}_{1} } \\ {\dot{x}_{2} } \\ {\dot{x}_{3} } \\ {\dot{x}_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \alpha_{1} - \alpha_{2} b} & {\alpha_{1} } & 0 & 0 \\ {\alpha_{3} } & { - \alpha_{3} } & {\alpha_{4} } & 0 \\ 0 & { - \alpha_{5} } & { - \alpha_{6} } & 0 \\ 1 & 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ {x_{4} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { - \alpha_{7} } \\ 0 \\ \end{array} } \right]\sin \left( {\sigma x_{1} \left( {t - \tau } \right)} \right).$$
(12)

Therefore, the final output of the fuzzy time delay memristor-based Chua’s circuit is derived as follows:

$$\begin{aligned} \dot{x}(t) & = M_{1} A_{1} x(t) + M_{2} A_{2} x(t) + df(x_{1} (t - \tau )) \\ & = \sum\limits_{i = 1}^{2} {M_{i} A_{i} x} + df(x_{1} (t - \tau )), \\ \end{aligned}$$
(13)

where

$$A_{1} = \left[ {\begin{array}{*{20}c} { - \alpha _{1} - \alpha _{2} a} & {\alpha _{1} } & 0 & 0 \\ {\alpha _{3} } & { - \alpha _{3} } & {\alpha _{4} } & 0 \\ 0 & { - \alpha _{5} } & { - \alpha _{6} } & 0 \\ 1 & 0 & 0 & 0 \\ \end{array} } \right],\,A_{2} = \left[ {\begin{array}{*{20}c} { - \alpha _{1} - \alpha _{2} b} & {\alpha _{1} } & 0 & 0 \\ {\alpha _{3} } & { - \alpha _{3} } & {\alpha _{4} } & 0 \\ 0 & { - \alpha _{5} } & { - \alpha _{6} } & 0 \\ 1 & 0 & 0 & 0 \\ \end{array} } \right],\,{\text{and }}d = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { - \alpha _{7} } \\ 0 \\ \end{array} } \right]$$

and state vector \(x(t) = [x_{1} (t),x_{2} (t),x_{3} (t),x_{4} (t)]^{T}\) and \(f(x_{1} (t - \tau )) = \sin (x_{1} (t - \tau ))\). Based on this fuzzy model, complex chaotic behavior of the time delay memristor-based Chua’s circuit can be simplified by only two nonlinear subsystems. With a center average defuzzifier, the fuzzy system is represented as

$$\dot{x}\left( t \right) = \sum\limits_{i = 1}^{2} {\beta_{i} A_{i} x\left( t \right)} + df\left( {x_{1} \left( {t - \tau } \right)} \right),$$
(14)

where \(\beta_{i} = M_{i} \left( {M_{1} + M_{2} } \right)^{ - 1}\). From (9), \(M_{1} + M_{2} = 1\), we have \(\beta_{i} =\) \(M_{i}\).

To confirm the effectiveness of the proposed fuzzy model (14), the following parameter values and initial conditions are chosen as \(C_{1} = 0.1\), \(C_{2} = 1\), \(L = \frac{1}{18}\), \(\, r = \frac{1}{45}\), \(R = 1\), \(a = 0.3\), \(b = 0.8\), \(\varepsilon = 3, \, \sigma = 5, \, \tau = 0.1\), and \(x(0) = [0.1, \, 0.1,\) \(\, 0.1, \, 0.1]\). The 3D phase portraits of \(x_{1} - x_{2} - x_{3}\) and \(x_{1} - x_{2} - x_{4}\) are given in Fig. 5. The dynamical behaviors of \(x_{1}\), \(x_{2}\), \(x_{3} ,\) and \(x_{4}\) are shown in Fig. 6. We can see that the dynamical behaviors of the time delay memristor-based Chua’s circuit can be exactly predicted by T–S fuzzy model.

Fig. 5
figure 5

The 3D phase portraits of \(x_{1} - x_{2} - x_{3}\) and \(x_{1} - x_{2} - x_{4}\)

Full size image
Fig. 6
figure 6

The dynamical behaviors of \(x_{1}\), \(x_{2}\), \(x_{3} ,\) and \(x_{4}\)

Full size image

3 Fuzzy Synchronization of two Different Delay Memristor-Based Chua’s Circuits

In this section, the main objective is to design a fuzzy control vector \(u(t) = [u_{1} (t),u_{2} (t),u_{3} (t),u_{4} (t)]^{T}\) to synchronize drive and response time delay memristor-based Chua’s circuits. To begin with, consider the drive and response time delay memristor-based Chua’s circuits as follows:Drive system:

$$\dot{x}\left( t \right) = \sum\limits_{i = 1}^{2} {\beta_{xi} A_{xi} x\left( t \right)} + d_{x} f_{x} \left( {x_{1} \left( {t - \tau_{x} } \right)} \right)$$
(15)

Response system:

$$\dot{y}\left( t \right) = \sum\limits_{i = 1}^{2} {\beta_{yi} A_{yi} y\left( t \right)} + d_{y} f_{y} \left( {y_{1} \left( {t - \tau_{y} } \right)} \right) + Bu\left( t \right),$$
(16)

where state vector \(y(t) = [y_{1} (t),y_{2} (t),y_{3} (t),y_{4} (t)]^{T}\). Subtracting the drive system (15) from the response system (16), the following error system can be obtained.

$$\begin{aligned} \dot{e}\left( t \right) & = \dot{x}\left( t \right) - \dot{y}\left( t \right) \\ & = \sum\limits_{i = 1}^{2} {\beta_{xi} A_{xi} x\left( t \right)} + {\text{d}}_{x} f_{x} \left( {x_{1} \left( {t - \tau_{x} } \right)} \right) - \sum\limits_{i = 1}^{2} {\beta_{yi} A_{yi} y\left( t \right)} - {\text{d}}_{y} f_{y} \left( {y_{1} \left( {t - \tau_{y} } \right)} \right) - Bu\left( t \right), \\ \end{aligned}$$
(17)

where error signal vector \(e\left( t \right) = [e_{1} (t),e_{2} (t),e_{3} (t),e_{4} (t)]^{T} = x\left( t \right) - y\left( t \right)\). Following the preceding analysis, we introduce the following theorem.

Theorem

Consider the drive system and response system given in (15) and (16), respectively. If the fuzzy control vector is expressed as

$$\begin{aligned} u\left( t \right) & = \sum\limits_{i = 1}^{2} {\beta_{xi} \varPsi_{xi} x\left( t \right)} + \varLambda_{x} f_{x} \left( {x_{1} \left( {t - \tau_{x} } \right)} \right) - \sum\limits_{i = 1}^{2} {\beta_{yi} \varPsi_{yi} y\left( t \right)} \\ & - \varLambda_{y} f_{y} \left( {y_{1} \left( {t - \tau_{y} } \right)} \right) \\ \end{aligned}$$
(18)

and the following conditions can be satisfied

$$A_{xi} - B\varPsi_{xi} = A_{yi} - B\varPsi_{yi} = F < 0, \, i = 1,2.,\quad d_{x} - B\varLambda_{x} = d_{y} - B\varLambda_{y} = 0$$
(19)

where \(\varPsi_{xi}\) and \(\varPsi_{yi}\) are the feedback gain matrices. \(\varLambda_{x}\) and \(\varLambda_{y}\) are constant gain vectors. The error system is asymptotically stable and the response system (16) can synchronize with the drive system (15).

Proof

To begin with, by substituting control vector (18) into the error system (17), (17) can be rewritten as

$$\begin{aligned} \dot{e}\left( t \right) & = \dot{x}\left( t \right) - \dot{y}\left( t \right) = \sum\limits_{i = 1}^{2} {\beta_{xi} \left( {A_{xi} - B\varPsi_{xi} } \right)x\left( t \right)} - \sum\limits_{i = 1}^{2} {\beta_{yi} \left( {A_{yi} - B\varPsi_{yi} } \right)y\left( t \right)} \\ & + \left( {d_{x} - B\varLambda_{x} } \right)f_{x} \left( {x_{1} \left( {t - \tau_{x} } \right)} \right) - \left( {d_{y} - B\varLambda_{y} } \right)f_{y} \left( {y_{1} \left( {t - \tau_{y} } \right)} \right). \\ \end{aligned}$$
(20)

Based on the conditions (19), the feedback gain matrices \(\varPsi_{xi}\) and \(\varPsi_{yi}\) can be obtained as

$$\left\{ \begin{aligned} & \varPsi_{xi} = B^{ - 1} (A_{xi} - F) \\ & \varPsi_{yi} = B^{ - 1} (A_{yi} - F) \\ \end{aligned} \right..$$
(21)

Simultaneously, the constant gain matrices \(\varLambda_{x}\) and \(\varLambda_{y}\) can be derived as

$$\left\{ \begin{aligned} \varLambda_{x} = B^{ - 1} d_{x} \hfill \\ \varLambda_{y} = B^{ - 1} d_{y} \hfill \\ \end{aligned} \right..$$
(22)

Therefore, the error system can be converted to the following form.

$$\dot{e}\left( t \right) = \sum\limits_{i = 1}^{2} {\beta_{xi} Fx\left( t \right)} - \sum\limits_{i = 1}^{2} {\beta_{yi} F} y\left( t \right) = Fe\left( t \right).$$
(23)

As a result, the error system is asymptotically stable, i.e., \(e_{1} (t) \to 0\), \(e_{2} (t) \to 0\), \(e_{3} (t) \to 0\), \(e_{4} (t) \to 0\) as \(t \to \infty\). The proof is completed.□

4 Simulation Examples

In this section, we will apply our fuzzy controller to synchronize drive and response time delay memristor-based Chua’s circuits. Moreover, the proposed synchronization approach will be used to realize its application in secure communication.

Example 1

Consider the drive system and response system given in (14) and (15), respectively. For this numerical simulation, the initial conditions and parameter values are given asDrive system:

$$\left\{ \begin{aligned} & C_{x1} = 0.1, \, C_{x2} = 1, \, L_{x} = \frac{1}{18}, \, r_{x} = \frac{1}{45}, \, R_{x} = 1,a_{x} = 0.3 \, \\ & b_{x} = 0.8,\,\varepsilon_{x} = 3, \, \sigma_{x} = 5, \, \tau_{x} = 0.1,\,x(0) = [0.1, \, 0.1, \, 0.1, \, 0.1]^{T} \\ \end{aligned} \right.$$

Response system:

$$\left\{ \begin{aligned} & C_{y1} = 0.2, \, C_{y2} = 1.2, \, L_{y} = 0.05, \, r_{y} = 0.02, \, R_{y} = 1.2,\,a_{y} = 3 \, \\ & b_{y} = 5,\varepsilon_{y} = 1, \, \sigma_{y} = 3, \, \tau_{y} = 0.01,y(0) = [0.3, \, 0.3, \, 0.3, \, 0.3]^{T} \\ \end{aligned} \right..$$

If \(F = - I_{4 \times 4}\) and \(B = I_{4 \times 4}\) are chosen, the feedback gains and constant matrices can be determined as

$$\varPsi_{x1} = \left[ {\begin{array}{*{20}c} { - 12} & {10} & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & { - 18} & {0.6} & 0 \\ 1 & 0 & 0 & 1 \\ \end{array} } \right], \, \varPsi_{x2} = \left[ {\begin{array}{*{20}c} { - 17} & {10} & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & { - 18} & {0.6} & 0 \\ 1 & 0 & 0 & 1 \\ \end{array} } \right]$$
$$\varLambda_{x} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { - 54} \\ 0 \\ \end{array} } \right],\quad \varPsi_{y1} = \left[ {\begin{array}{*{20}c} { - 18.166} & {4.166} & 0 & 0 \\ {0.6944} & {0.305} & {0.833} & 0 \\ 0 & { - 20} & {0.6} & 0 \\ 1 & 0 & 0 & 1 \\ \end{array} } \right]$$
$$\varPsi_{y2} = \left[ {\begin{array}{*{20}c} { - 28.166} & {4.166} & 0 & 0 \\ {0.6944} & {0.305} & {0.833} & 0 \\ 0 & { - 20} & {0.6} & 0 \\ 1 & 0 & 0 & 1 \\ \end{array} } \right], \, \varLambda_{y} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { - 20} \\ 0 \\ \end{array} } \right].$$

The 3D phase portraits and 2D projections before synchronization are shown in Fig. 7. The synchronization performance, the 3D phase portraits, and 2D projection, after fuzzy control vector is applied to the response system, are depicted in Fig. 8. The dynamical behaviors of (\(x_{1}\), \(x_{2}\), \(x_{3}\), \(x_{4}\)) and (\(y_{1}\), \(y_{2}\), \(y_{3}\), \(y_{4}\)) are given in Fig. 9, and the synchronization errors \(e_{1} (t)\), \(e_{2} (t)\), \(e_{3} (t)\), \(e_{4} (t)\) are described in Fig. 10. The fuzzy control inputs \(u_{1} (t)\), \(u_{2} (t)\), \(u_{3} (t)\), \(u_{4} (t)\) are exhibited in Fig. 11.

Fig. 7
figure 7

The 3D phase portraits and 2D projections before synchronization

Full size image
Fig. 8
figure 8

The 3D phase portraits and 2D projections after synchronization

Full size image
Fig. 9
figure 9

The dynamical behaviors of (\(x_{1}\), \(x_{2}\), \(x_{3}\), \(x_{4}\)) and (\(y_{1}\), \(y_{2}\), \(y_{3}\), \(y_{4}\))

Full size image
Fig. 10
figure 10

The synchronization errors \(e_{1} (t)\), \(e_{2} (t)\), \(e_{3} (t)\), \(e_{4} (t)\)

Full size image
Fig. 11
figure 11

The control inputs \(u_{1} (t)\), \(u_{2} (t)\), \(u_{3} (t)\), \(u_{4} (t)\)

Full size image

From Figs. 8, 9 and 10, it is obvious that drive and response systems are synchronized instantly when the fuzzy control vector is applied to the response system.

Example 2

In this example, we will apply our fuzzy modeling chaotic synchronization scheme to secure communication, thanks to the dynamical behavior with complex transient transitions of the memristor-based chaotic system which is heavily dependent on the initial state of the memristor except for the circuit parameters. Therefore, the memristor-based chaotic system can generate more complex and unpredictable time domain signals. The drive system and response system are given in (15) and (16), respectively, and all the system parameters are chosen as given in example 1. Figure 12 depicts a block diagram of the secure communication based on the time delay memristor-based Chua’ circuits.

Fig. 12
figure 12

The block diagram of the secure communication based on the time delay memristor-based Chua’ circuits

Full size image

As an example, we consider an image of a rabbit and a cat as shown Fig. 13a2. To send the above image using the proposed synchronization scheme, the image must be digitized to become a digital information signal (0–255 levels) as shown in Fig. 13a1. The encrypted signal is shown in Fig. 13b. The decrypted signals, i.e., received signals, are shown in Fig. 13c. We can see that the transmitted digital information signal can be decrypted perfectly.

Fig. 13
figure 13

Signal encryption and recovery with memristor-based time delay Chua’s chaotic circuits

Full size image

Remarks

  1. 1.

    The memristor-based chaotic system can enable more complex and unpredictable time domain signals because the memory of initial state of the memristor plays a significantly important role in producing complicated transient transition dynamics.

  2. 2.

    Based on our design scheme, the transmitted signals not only are complex and unpredictable but also have stronger anti-attack ability and anti-translated capability than that transmitted by the other existing transmission model.

5 Conclusions

In this paper, based on T-S fuzzy modeling, chaotic synchronization of two different time delay memristor-based Chua’s circuits has been proposed and three main contributions are achieved as follows:

  1. (1)

    The fuzzy model of the time delay memristor-based Chua’s circuit is constructed only by two simplified nonlinear subsystems.

  2. (2)

    The fuzzy control vector is derived to synchronize two different time delay memristor-based Chua’s circuits.

  3. (3)

    The proposed fuzzy modeling chaotic synchronization scheme is applied to secure communication.

Simulation results show that the dynamical behaviors of the time delay memristor-based Chua’s circuit can be exactly predicted by T–S fuzzy model and a secure communication application is performed to confirm that the transmitted digital information signal can be decrypted perfectly using the proposed chaotic synchronization scheme.

Furthermore, in general, time delays mainly exist in the communication channel or control terminal as the lag between the state output node and feedback channel. It is natural to consider time delay when dealing with synchronization problems within chaotic systems, i.e., lag synchronization, where the corresponding state vectors of response system follow the drive system with time delay, will be considered in the future work. In the meantime, the results of this paper will be extended to the interval type-2 FNN, as type-1 fuzzy logic control cannot fully handle or accommodate the linguistic and numerical uncertainties associated with dynamic unstructured environments.