Abstract
As mobile commerce (m-commerce) has continued to grow via advancements in wireless and mobile technology, the issue of m-commerce has become more significant. To improve m-commerce adoption, companies should establish a perfect m-commerce environment and learn to understand consumer needs. This paper proposes an evaluation model for m-commerce that can explore and improve m-commerce adoption for uncertain information in a fuzzy environment. The model addresses the interdependence and feedback effects between criteria or dimensions, the best alternative selection and systematic improvement by adopting a new hybrid fuzzy MADM model, which uses the fuzzy DEMATEL technique to construct the fuzzy INRM and determine the fuzzy influential weights using the fuzzy DANP. It further combines the fuzzy VIKOR methods for creating the best improvement plan based on the fuzzy INRM. An empirical case for evaluating m-commerce adoption is used to verify the proposed planning model. The results reveal that the proposed planning model can help companies improve m-commerce adoption for enhancing consumer trust via integrity.





Similar content being viewed by others
References
Chong, A.Y.L.: Predicting m-commerce adoption determinants: a neural network approach. Expert Syst. Appl. 40(2), 523–530 (2013)
Lu, M.T., Tang, L.L., Tzeng, G.H.: Environmental strategic orientations for improving green innovation performance in fuzzy environment—using new fuzzy hybrid MCDM model. Int. J. Fuzzy Syst. 15(3), 297–316 (2013)
Hsieh, T.Y., Lu, S.T., Tzeng, G.H.: Fuzzy MCDM approach for planning and design tenders selection in public office buildings. Int. J. Project Manag. 22(7), 573–584 (2004)
Tzeng, G.H., Huang, J.J.: Multiple Attribute Decision Making: Methods and Applications. CRC Press, New York (2011)
Tzeng, G.H., Huang, J.J.: Fuzzy Multiple Objective Decision Making. CRC Press, New York (2013)
Chen, V.Y.C., Lien, H.P., Liu, C.H., Liou, J.J.H., Tzeng, G.H., Yang, L.S.: Fuzzy MCDM approach for selecting the best environment-watershed plan. Appl. Soft Comput. 11(1), 265–275 (2011)
Büyüközkan, G., Çifçi, G.: A combined fuzzy AHP and fuzzy TOPSIS based strategic analysis of electronic service quality in healthcare industry. Expert Syst. Appl. 39(3), 2341–2354 (2012)
Calabrese, A., Costa, R., Menichini, T.: Using Fuzzy AHP to manage Intellectual Capital assets: an application to the ICT service industry. Expert Syst. Appl. 40(9), 3747–3755 (2013)
Büyüközkan, G.: Determining the mobile commerce user requirements using an analytic approach. Comput. Stand. Interfaces 31(1), 144–152 (2009)
Lin, J., Lu, Y., Wang, B., Wei, K.K.: The role of inter-channel trust transfer in establishing mobile commerce trust. Electron. Commer. Res. Appl. 10(6), 615–625 (2011)
Chong, A.Y.L.: A two-staged SEM-neural network approach for understanding and predicting the determinants of m-commerce adoption. Expert Syst. Appl. 40(4), 1240–1247 (2013)
Simon, H.A.: Theories of bounded rationality. In: McGuire, C.B., Radner, R. (eds.) Decision and Organization, pp. 161–176. North-Holland, Amsterdam (1972)
Barnes, S.J.: The mobile commerce value chain: analysis and future developments. Int. J. Inf. Manag. 22(2), 91–108 (2002)
Ngai, E.W.T., Gunasekaran, A.: A review for mobile commerce research and applications. Decis. Support Syst. 43(1), 3–15 (2007)
Gefen, D., Karahanna, E., Straub, D.W.: Trust and TAM in online shopping: an integrated model. MIS Quart. 27(1), 51–90 (2003)
Pavlou, P.A., Fygenson, M.: Understanding and predicting electronic commerce adoption: an extension of the theory of planned behavior. MIS Quart. 30(1), 115–143 (2006)
Gefen, D., Straub, D.W.: Consumer trust in B2C e-commerce and the importance of social presence: experiments in e-products and e-services. Omega 32(6), 407–424 (2004)
Gefen, D., Benbasat, I., Pavlou, P.A.: A research agenda for trust in online environments. J. Manag. Inf. Syst. 24(4), 275–286 (2008)
Fang, Y., Qureshi, I., Sun, H., McCole, P., Ramsey, E., Lim, K.H.: A research agenda for trust in online environments. J. Manag. Inf. Syst. 24(4), 275–286 (2014)
Ajzen, I.: The theory of planned behavior. Organ. Behav. Hum. Decis. Process. 50(2), 179–211 (1991)
Taylor, S., Todd, P.: Decomposition and crossover effects in the theory of planned behavior: a study of consumer adoption intentions. Int. J. Res. Mark. 12(2), 137–155 (1995)
Liao, S., Shao, Y.P., Wang, H., Chen, A.: The adoption of virtual banking: an empirical study. Int. J. Inf. Manag. 19(1), 63–74 (1999)
Davis, F.D.: Perceived usefulness, perceived ease of use, and user acceptance of information technology. MIS Quart. 13(3), 319–340 (1989)
Davis, F.D., Bagozzi, R.P., Warshaw, P.R.: User acceptance of computer technology: a comparison of two theoretical models. Manag. Sci. 35(8), 982–1003 (1989)
Pynpoo, B., van Braak, J.: Predicting teachers’ generative and receptive use of an educational portal by intention, attitude and self-reported use. Comput. Hum. Behav. 34, 315–322 (2014)
Kuo, Y.F., Chen, P.C.: Selection of mobile value-added services for system operators using fuzzy synthetic evaluation. Expert Syst. Appl. 30(4), 612–620 (2006)
Kuo, Y.F., Yen, S.N.: Towards an understanding of the behavioral intention to use 3G mobile value-added services. Comput. Hum. Behav. 25(1), 103–110 (2009)
Kuo, Y.F., Wu, C.M., Deng, W.J.: The relationships among service quality, perceived value, customer satisfaction, and post-purchase intention in mobile value-added services. Comput. Hum. Behav. 25(4), 887–896 (2009)
Bouwman, H., Bejar, A., Nikou, S.: Mobile services put in context: a Q-sort analysis. Telematics Inform. 29(1), 66–81 (2012)
Nikou, S., Mezei, G.: Evaluation of mobile services and substantial adoption factors with analytic hierarchy process (AHP). Telecommun. Policy 37(10), 915–929 (2013)
Zadeh, L.A.: The concept of a linguistic variable and its application to approximate reasoning. Inf. Sci. 8(3), 199–249 (1975)
Dubois, D., Prade, H.: Operations on fuzzy numbers. Int. J. Syst. Sci. 9(6), 613–626 (1978)
van Laarhoven, P.J.M., Pedrycz, W.: A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 11(1–3), 199–227 (1983)
Hsu, C.Y., Chen, K.T., Tzeng, G.H.: FMCDM with fuzzy DEMATEL approach for customers’ choice behavior model. Int. J. Fuzzy Syst. 4(4), 236–246 (2007)
Opricovic, S., Tzeng, G.H.: Defuzzification within a fuzzy multicriteria decision model. Int. J. Uncertain. Fuzz Knowl.-Based Syst. 11(5), 635–652 (2003)
Watson, C., McCarthy, J., Rowley, J.: Consumer attitudes towards mobile marketing in the smart phone era. Int. J. Inf. Manag. 33(5), 840–849 (2013)
Saaty, T.L.: Decision Making with Dependence and Feedback: The Analytic Network Process. RWS Publications, Pittsburgh (1996)
Zadeh, L.A.: Fuzzy sets. Inf. Control 8(2), 338–353 (1965)
Bellman, R.E., Zadeh, L.A.: Decision-making in a fuzzy environment management. Science 17(4), 141–164 (1970)
Author information
Authors and Affiliations
Corresponding author
Appendix: Hybrid Fuzzy MADM Model Based on the Fuzzy DANP and Fuzzy VIKOR
Appendix: Hybrid Fuzzy MADM Model Based on the Fuzzy DANP and Fuzzy VIKOR
1.1 Appendix 1: The Fuzzy DEMATEL Technique
The technique is described as follows:
Step 1 Calculate the fuzzy direct relation average matrix.
The fuzzy direct relation average matrix \( \tilde{\varvec{A}} \) is given by Eq. (4), and membership functions of the linguistic scale in this paper are constructed using triangular fuzzy numbers, as shown in Table 7, where \( \tilde{\varvec{A}} = [\tilde{a}_{ij} ]_{n \times n} = [(a_{ij}^{l} ,a_{ij}^{m} ,a_{ij}^{h} )]_{n \times n} , \) \( \tilde{a}_{ij} \) represents the fuzzy degree of direct influence of criterion \( i \) on criterion \( j \).
Step 2 Calculate the fuzzy initial influence matrix.
The fuzzy initial influence matrix \( \tilde{\varvec{E}} \) can be obtained by normalizing matrix \( \tilde{\varvec{A}} \). In addition, matrix \( \tilde{\varvec{E}} \) can be obtained by Eqs. (5) and (6), in which the main diagonal criteria are equal to zero.
where \( \tilde{\varvec{E}} = [\tilde{e}_{ij} ]_{n \times n} = [(e_{ij}^{l} ,e_{ij}^{m} ,e_{ij}^{h} )]_{n \times n} \), \( (0,0,0) \le \tilde{e}_{ij} < (1,1,1) \), \( (0,0,0) < \sum\nolimits_{j = 1}^{n} {\tilde{e}_{ij} } ,\sum\nolimits_{i = 1}^{n} {\tilde{e}_{ij} } \le (1,1,1) \), and \( i, \, j = 1,2,\ldots,n \); If at least one row or column of summation is equal to 1 (but not all) in \( \sum\nolimits_{j = 1}^{n} {\tilde{e}_{ij} } \) and \( \sum\nolimits_{i = 1}^{n} {\tilde{e}_{ij} } \), we can guarantee \( \lim_{x \to \infty } \tilde{\varvec{E}}^{x} = [\tilde{0}]_{n \times n} = [(0,0,0)]_{n \times n} \).
Step 3 Calculate the fuzzy total influence matrix.
The fuzzy total influence matrix \( \tilde{T} \) can be obtained by the infinite series of direct and indirect effects for matrix \( \tilde{E} \). In addition, matrix \( \tilde{T} \) can be obtained by Eq. (A4), in which \( I \) is an identity matrix.
where \( \tilde{\varvec{T}} = [\tilde{t}_{ij} ]_{n \times n} = [t_{ij}^{l} ,t_{ij}^{m} ,t_{ij}^{h} ]_{n \times n} \), \( i, \, j = 1,2,\ldots,n \) and \( \varvec{I} = (\varvec{I}\Uptheta \tilde{\varvec{E}}) \otimes (\varvec{I}\Uptheta \tilde{\varvec{E}})^{ - 1} \).
Step 4 Construct the fuzzy INRM.
According to Eqs. (8) and (9), the sum of each row and column for matrix \( \tilde{T} \) can be obtained, where \( \tilde{r}_{i} \) denotes the sum of the ith row of matrix \( \tilde{T} \) and shows the sum of the direct and indirect effects that criterion \( i \) influences other criteria, and \( \tilde{c}_{j} \) denotes the sum of the jth column of the matrix \( \tilde{T} \) and shows the sum of the direct and indirect effects that criterion \( j \) is influenced by other criteria. When \( i \) equals \( j \), \( \tilde{r}_{i} \oplus \tilde{c}_{i} \) represents an index of the strength of influence given and received and shows the degree of the central role that criterion \( i \) plays in the problem. In addition, \( \tilde{r}_{i} \Uptheta \tilde{c}_{i} \) represents the degree of causality among criteria. Based on matrix \( \tilde{T} \), the fuzzy INRM can be constructed by the fuzzy degrees of influence and causality.
where vector \( \tilde{\varvec{r}} \) and \( \tilde{\varvec{c}} \) denote the sum of vector row and column, respectively, \( i, \, j \in \{ 1,2,\ldots,n\} \).
1.2 Appendix 2: The Fuzzy DANP Method
The method is described as follows:
Step 1 Construct the fuzzy un-weighted super-matrix.
The fuzzy total influence matrix can be measured by criteria, as shown in matrix \( \tilde{\varvec{T}}_{C} \) in Eq. (10). Matrix \( \tilde{\varvec{T}}_{C}^{\alpha } \) can be obtained from a normalized matrix \( \tilde{\varvec{T}}_{C} \) with the total degree of effect of dimensions, as shown in Eq. (11). Next, the fuzzy un-weighted super-matrix \( \tilde{\varvec{W}} \) can be obtained by transposing matrix \( \tilde{\varvec{T}}_{C}^{\alpha } \), as shown in Eq. (12).



Step 2 Determine the fuzzy weighted super-matrix matrix.
The fuzzy total influence matrix can be measured by dimension, as shown in matrix \( \tilde{\varvec{T}}_{D} \) in Eq. (13). Matrix \( \tilde{\varvec{T}}_{D}^{\alpha } \) can be obtained from a normalized matrix \( \tilde{\varvec{T}}_{D} \) with the total degree of effect, as shown Eq. (14). The normalized matrix \( \tilde{\varvec{T}}_{D}^{\alpha } \) and the un-weighted super-matrix \( \tilde{\varvec{W}} \) are used to yield the weighted super-matrix \( \tilde{\varvec{W}}^{\alpha } \), as shown Eq. (15).
Step 3 Calculate the fuzzy influential weights.
The fuzzy weighted super-matrix \( \tilde{\varvec{W}}^{\alpha } \) is multiplied by itself multiple times to obtain the fuzzy limit weighted super-matrix \( \mathop {\lim }\nolimits_{\beta \to \infty } ({\tilde{\mathbf{W}}}^{\alpha } )^{\beta } \). Then, the fuzzy influential weights can be calculated with \( \mathop {\lim }\nolimits_{\beta \to \infty } ({\tilde{\mathbf{W}}}^{\alpha } )^{\beta } \) until the super-matrix has converged and become a stable super-matrix, where \( \beta \) represents a positive integer number.
1.3 Appendix 3: The Fuzzy VIKOR Method
The expansion of the fuzzy VIKOR method began with the following form of the \( \tilde{L}_{k}^{p} \) metric:
where \( \tilde{r}_{kj} \) is the fuzzy gap (i.e., fuzzy degrees of regret) of the \( j \)th criterion in the \( k \)th alternative, \( \tilde{w}_{j} \) is the influential weight of the \( j \)th criterion, \( \tilde{f}_{kj} \) is the performance score of the \( j \)th criterion in the \( k \)th alternative, \( \tilde{f}_{j}^{ * } \) is the best value (i.e., the aspiration level), and \( \tilde{f}_{j}^{ - } \) is the worst level, \( 1 \le p \le \infty \), \( j = 1,2,\ldots,n \), \( k = 1,2,\ldots,K \). The method is described as follows:
Step 1 Set the fuzzy aspiration level and worst level.
The proposed approach for improvement is given the fuzzy aspiration and worst level, as shown in Eqs. (18) and (19).
The fuzzy aspiration levels:
The fuzzy worst levels:
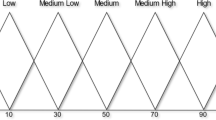
In this study, questionnaires use the measuring scores \( \tilde{0} \) to \( \tilde{4} \) (very bad ← \( \tilde{0} \),\( \tilde{1} \),\( \tilde{2} \),\( \tilde{3} \),\( \tilde{4} \) → very good) to evaluate the performances; therefore, the fuzzy aspiration level can be set at score \( \tilde{f}_{j}^{ * } = (f_{j}^{ * l} ,f_{j}^{ * m} ,f_{j}^{ * h} ) = (4,4,4) \) and the fuzzy worst level, at score \( \tilde{f}_{j}^{ - } = (f_{j}^{ - l} ,f_{j}^{ - m} ,f_{j}^{ - h} ) = (0,0,0) \). This approach can avoid “picking the best apple from a barrel of rotten apples.” Membership functions of linguistic scale for questionnaires are constructed using triangular fuzzy numbers, as shown in Table 8.
Step 2 Calculate the fuzzy group utility and individual maximum regret.
The fuzzy group utility \( \tilde{G}_{k} \) and individual maximum regret \( \tilde{M}_{k} \) for gap measures can be formulated using the concept (\( \tilde{L}_{k}^{p = 1} \) and \( \tilde{L}_{k}^{p = \infty } \)) of the fuzzy VIKOR method, respectively, as shown in Eqs. (20) and (21). The compromise solution \( \min_{k} \tilde{L}_{k}^{p} \) (i.e., \( \min_{k} \tilde{G}_{k} ) \) minimizes the integrating gap (i.e., the average gap), which will be improved to ensure a value closest to the aspiration level. In addition, the fuzzy group utility is emphasized to make p small (e.g., p = 1); if p tends toward infinity, the fuzzy individual maximum regrets/gaps receive a greater priority in the improvement of each dimension/criterion.
Step 3 Calculate the fuzzy comprehensive indicators.
The fuzzy comprehensive indicators \( \tilde{R}_{k} \) for improving and ranking the results can be obtained with Eq. (22). Therefore, \( \tilde{R}_{k} \) can be considered the basis of the ranking/improving alternatives when \( \tilde{R}_{k} \) is close to zero (i.e., close to the aspiration level).
where \( v \) represents the weight of the strategy. Generally, \( v = 0.5 \), which can be adjusted depending on the case under consideration from the view-points for various options; \( v = 1 \) indicates that only the average gap is considered, and \( v = 0 \) indicates that only the fuzzy individual maximum regret/gap is prioritized for improvement. Eq. (22) also can be rewritten as \( \tilde{R}_{k} = v \odot \tilde{G}_{k} \oplus (1 - v) \odot \tilde{M}_{k} , \) when the fuzzy best gap is \( \tilde{G}^{*} = (0,0,0) \) and the fuzzy worst gap \( \tilde{G}^{ - } = (1,1,1) \) in the average gap, and the fuzzy best gap is \( \tilde{M}^{*} = (0,0,0) \) and the fuzzy worst gap \( \tilde{M}^{ - } \; = \;(1,1,1) \) in the individual maximum gap.
Rights and permissions
About this article
Cite this article
Hu, Sk., Lu, MT. & Tzeng, GH. Improving Mobile Commerce Adoption Using a New Hybrid Fuzzy MADM Model. Int. J. Fuzzy Syst. 17, 399–413 (2015). https://doi.org/10.1007/s40815-015-0054-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40815-015-0054-z
Keywords
- Mobile commerce adoption
- Fuzzy MADM (fuzzy multiple attribute decision making)
- Fuzzy DEMATEL (fuzzy decision making trial and evaluation laboratory)
- Fuzzy INRM (fuzzy influential network relationship map)
- Fuzzy DANP (fuzzy DEMATEL-based analytic network process)
- Fuzzy VIKOR (fuzzy VlseKriterijumska Optimizacija I Kompromisno Resenje)