Abstract
To enable efficient association rule mining, existing techniques prestore intermediate results as itemsets. However, the actual rule generation is still performed at query-time. The response time thus tends to remain unacceptably long for interactive mining, especially when rule redundancy resolution is required. Further, the widespread restriction to only support positive rules can miss important insights and lead to misleading results. For this reason, the discovery of both negative and positive rules, which can be extremely revealing, is important. Unfortunately, the generation of negative rules slows down the mining process even further. To tackle these shortcomings, we introduce the parameter space model, called \({\textbf {PARAS}}^{{\textbf {c}}}\). \({\textbf {PARAS}}^{{\textbf {c}}}\) enables efficient mining of complete rules, i.e., both positive and negative rules, by precomputing and compactly maintaining the final rulesets. The \({\textbf {PARAS}}^{{\textbf {c}}}\) model is based on the stable region abstractions that form the coarse granularity ruleset space for managing complete rules. Based on new insights into the redundancy relationships among complete rules, \({\textbf {PARAS}}^{{\textbf {c}}}\) establishes a surprisingly compact representation of complex redundancy relationships while enabling efficient redundancy resolution for complete rules at query-time. \({\textbf {PARAS}}^{{\textbf {c}}}\) supports novel classes of exploratory queries that can be answered near real time. Our experimental evaluation demonstrates that \({\textbf {PARAS}}^{{\textbf {c}}}\) achieves 2–5 orders of magnitude improvement over existing techniques in rule mining.

























Similar content being viewed by others
Notes
Hindi name for a legendary philosopher’s stone said to be capable of turning base metals (lead, for example) into gold.
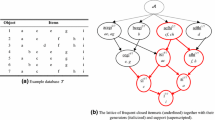
Multiple rules may map to the simple/strict dominating location that collectively represents them.
Rule \({\mathcal {R}}_{31}\) and its simple dominating rules \(\{{\mathcal {R}}_{31}^{\gg _{sim}}\}\) are also \({\mathcal {R}}_{16}\)’s strict dominating rules. That is, \(\{{\mathcal {R}}_{16}^{\gg _{str}}\} = \{{\mathcal {R}}_{31}\} \cup \{{\mathcal {R}}_{31}^{\gg _{sim}}\}\).
The number of strict dominating location(s) is up to 2 by our experiment.
Some dominating rules may not be valid because their lift values do not satisfy minimum lift.
An i-antecedent rule only has i-antecedent items out of n.
Some simple dominating rules may not be valid because their lift values do not satisfy minimum lift.
References
Agrawal, R., Srikant, R.: Fast algorithms for mining association rules in large databases. In: Proceedings of the 20th International Conference on Very Large Databases, pp. 487–499 (1994)
Han, J., Fu, Y.: Discovery of multiple-level association rules from large databases. In: Proceedings of the 21th International Conference on Very Large Databases, pp. 420–431 (1995)
Lucchese, C., Orlando, S., Perego, R., Silvestri, F.: Webdocs: a real-life huge transactional dataset. In: Proceedings of the IEEE ICDM Workshop on Frequent Itemset Mining Implementations (2004)
Li, J., Le, T.D., Liu, L., Liu, J., Jin, Z., Sun, B., Ma, S.: From observational studies to causal rule mining. ACM Trans. Intell. Syst. Technol. 7(2), 14–11427 (2016)
Simon, G.J., Caraballo, P.J., Therneau, T.M., Cha, S.S., Castro, M.R., Li, P.W.: Extending association rule summarization techniques to assess risk of diabetes mellitus. IEEE Trans. Knowl. Data Eng. 27(1), 130–141 (2015)
Peng, M., Sundararajan, V., Williamson, T., Minty, E.P., Smith, T.C., Doktorchik, C.T.A., Quan, H.: Exploration of association rule mining for coding consistency and completeness assessment in inpatient administrative health data. J. Biomed. Inform. 79, 41–47 (2018)
Abar, O., Charnigo, R.J., Rayapati, A., Kavuluru, R.: On interestingness measures for mining statistically significant and novel clinical associations from emrs. In: Proceedings of the 7th ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics. BCB ’16, pp. 587–594 (2016)
Wong, P.-Y., Chan, T.-M., Wong, M.-H., Leung, K.-S.: Predicting approximate protein-dna binding cores using association rule mining. In: IEEE 28th International Conference on Data Engineering, pp. 965–976 (2012)
Aggarwal, C.C., Yu, P.S.: A new approach to online generation of association rules. IEEE Trans. Knowl. Data Eng. 13(4), 527–540 (2001)
Han, J., Pei, J., Yin, Y.: Mining frequent patterns without candidate generation. In: Proceedings of the ACM SIGMOD International Conference on Management of Data, pp.1–12 (2000)
Zaki, M.J., Parthasarathy, S., Ogihara, M., Li, W.: New algorithms for fast discovery of association rules. In: Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mining, pp. 283–286 (1997)
Brin, S., Motwani, R., Silverstein, C.: Beyond market baskets: Generalizing association rules to correlations. In: Proceedings of the ACM SIGMOD International Conference on Management of Data, pp. 265–276 (1997)
Aggarwal, C.C., Yu, P.S.: A new framework for itemset generation. In: Proceedings of the Seventeenth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, pp. 18–24 (1998)
Wu, X., Zhang, C., Zhang, S.: Efficient mining of both positive and negative association rules. ACM Trans. Inf. Syst. 22(3), 381–405 (2004)
Dong, X., Hao, F., Zhao, L., Xu, T.: An efficient method for pruning redundant negative and positive association rules. Neurocomputing 393, 245–258 (2020)
Hämäläinen, W.: Kingfisher: an efficient algorithm for searching for both positive and negative dependency rules with statistical significance measures. Knowl. Inf. Syst. 32(2), 383–414 (2012)
Hämäläinen, W., Webb, G.I.: Specious rules: an efficient and effective unifying method for removing misleading and uninformative patterns in association rule mining, In: Proceedings of the SIAM International Conference on Data Mining, pp. 309–317 (2017)
Kubat, M., Hafez, A., Raghavan, V.V., Lekkala, J.R., Chen, W.K.: Itemset trees for targeted association querying. IEEE Trans. Knowl. Data Eng. 15(6), 1522–1534 (2003)
Kaya, M., Alhajj, R.: Online mining of fuzzy multidimensional weighted association rules. Appl. Intell. 29, 13–34 (2008)
Dong, X., Niu, Z., Shi, X., Zhang, X., Zhu, D.: Mining both positive and negative association rules from frequent and infrequent itemsets. Adv. Data Min. Appl. 4632, 122–133 (2007)
Graham, R.L., Knuth, D.E., Patashnik, O.: Concrete Mathematics. Addison-Wesley, Boston (1994)
Lin, X., Mukherji, A., Rundensteiner, E.A., Ruiz, C., Ward, M.O.: Paras: Parameter space framework for online association mining. In: Proceedings of the VLDB Endowment, pp. 193–204 (2013)
Lin, X., Mukherji, A., Rundensteiner, E.A., Ward, M.O.: SPIRE: supporting parameter-driven interactive rule mining and exploration. PVLDB 7(13), 1653–1656 (2014)
Mukherji, A., Lin, X., Whitehouse, J., Botaish, C.R., Rundensteiner, E.A., Ward, M.O.: Fire: Interactive visual support for parameter space-driven rule mining. In: Proceedings of the 22nd ACM International Conference on Information & Knowledge Management, pp. 2447–2452 (2013)
Mukherji, A., Lin, X., Toto, E., Botaish, C.R., Whitehouse, J., Rundensteiner, E.A., Ward, M.O.: Fire: a two-level interactive visualization for deep exploration of association rules. Int. J. Data Sci. Anal. 7, 201–226 (2019)
Cornelis, C., Yan, P., Zhang, X., Chen, G.: Mining positive and negative association rules from large databases. In: 2006 IEEE Conference on Cybernetics and Intelligent Systems, pp. 1–6 (2006)
Asuncion, A., Newman, D.J.: UCI Machine Learning Repository. http://www.ics.uci.edu/~mlearn/MLRepository.html (2007)
Borgelt, C.: Efficient Implementations of Apriori, Eclat and FP-growth. http://www.borgelt.net (2012)
Savasere, A., Omiecinski, E., Navathe, S.: Mining for strong negative associations in a large database of customer transactions. In: ICDE, pp. 494–502 (1998)
Wang, S., Cao, L.: Inferring implicit rules by learning explicit and hidden item dependency. IEEE Trans. Syst. Man Cybern. Syst. 50(3), 935–946 (2020)
Cao, L.: Combined mining: analyzing object and pattern relations for discovering and constructing complex yet actionable patterns. WIREs Data Min. Knowl. Discov. 3(2), 140–155 (2013)
Wu, T., Chen, Y., Han, J.: Re-examination of interestingness measures in pattern mining: a unified framework. Data Min. Knowl. Discov. 21(3), 371–397 (2010)
Sahar, S.: Interestingness preprocessing. In: Proceedings of IEEE International Conference on Data Mining, pp. 489–496 (2001)
Li, J., Wang, C., Cao, L., Yu, P.S.: Efficient selection of globally optimal rules on large imbalanced data based on rule coverage relationship analysis. In: Proceedings of the 2013 SIAM International Conference on Data Mining, pp. 216–224 (2013)
Duan, S., Thummala, V., Babu, S.: Tuning database configuration parameters with ituned. PVLDB 2(1), 1246–1257 (2009)
Chaudhuri, S., Lee, H., Narasayya, V.R.: Variance aware optimization of parameterized queries. In: Proceedings of the ACM SIGMOD International Conference on Management of data, pp. 531–542 (2010)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supported by National Science Foundation under grants IIS-0812027, CCF-0811510 and IIS-1117139.
Appendix A
Appendix A
1.1 Proof to Lemma 8
Proof
Given a positive rule \({\mathcal {R}}\) contains only positive items, each simple dominating rule of \({\mathcal {R}}\) contains the same positive items as \({\mathcal {R}}\) (Definition 12). Thus it is also positive. Therefore, even when the scope of full-spectrum rule mining includes both positive and negative rules, a positive rule is only simply dominated by positive rules. \(\square \)
1.2 Proof to Lemma 9
Proof
Given a negative rule \({\mathcal {R}}\) contains at least one negative item, each simple dominating rule of \({\mathcal {R}}\) contains the same itemset (including the negative item(s)) as \({\mathcal {R}}\) (Definition 12). It is thus negative. Therefore, a negative rule is only simply dominated by negative rules. \(\square \)
1.3 Proof of Lemma 10
Proof
Given rule \({\mathcal {R}}\): (\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)) \(\rightarrow \) (\(\hbox {C}_{1}\):\(\hbox {C}_{m}\)), a 1-antecedent simple dominating ruleFootnote 7 is the rule using 1 item out of the set (\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)) as antecedent, the remaining (n-1) items (\(\hbox {A}_{v}\):\(\hbox {A}_{w}\)) along with (\(\hbox {C}_{1}\):\(\hbox {C}_{m}\)) as consequent. The total number of such 1-antecedent simple dominating rules for ((\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)) \(\rightarrow \) (\(\hbox {C}_{1}\):\(\hbox {C}_{m}\))) is up to \(\left( ^{n}_{1}\right) \).Footnote 8 Similarly, the number of 2-antecedent simple dominating rules is up to \(\left( ^{n}_{2}\right) \) \({}^{8}\) . Therefore, the number of simple dominating rules for ((\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)) \(\rightarrow \) (\(\hbox {C}_{1}\):\(\hbox {C}_{m}\))) is up to \(\sum _{i=1}^{n-1}\left( ^{n}_{i} \right) \) = 2\(^{n}\)-2. \(\square \)
1.4 Proof of Lemma 13
Proof
A positive rule \({\mathcal {R}}\) is generated from an itemset \(X_{j}\) consisting of only positive items. Each rule that strictly dominates \({\mathcal {R}}\) is constructed from an itemset \(X_{i}\), with \(X_{i}\supset X_{j}\). That is, \(X_{i}\) contains all items in \(X_{j}\) plus some additional items beyond \(X_{j}\) (Definition 13). If the additional items are all positive, then the formed strict dominating rule is positive, else it is negative. Therefore, a positive rule can be strictly dominated by both positive and negative rules. \(\square \)
1.5 Proof of Lemma 13
Proof
For a negative rule \({\mathcal {R}}\) generated from itemset \(X_{j}\) with at least one negative item, each of its strict dominating rules is generated from a superset of \(X_{j}\) (Definition 13). Each strict dominating rules of \({\mathcal {R}}\) thus also contains the same negative item(s). It is thus a negative rule. Thus, a negative rule can only be strictly dominated by negative rules. \(\square \)
1.6 Proof of Lemma 14
Proof
Given a strict dominated rule \({\mathcal {R}}\): (\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)) \(\rightarrow \) (\(\hbox {C}_{1}\):\(\hbox {C}_{m}\)), a 1-antecedent strict dominating rule is the rule using 1 item out of the set (\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)) as antecedent and adding w (\(1 \le w \le e\)) items from e additional items to the consequent. In the context of positive rules, for each additional item, there are 2 possibilities (positive form or not chosen). For a 1-antecedent strict dominating rule, there are \(2^{e}\) possibilities for adding items from e additional items to the consequent. The total of number of such 1-antecedent strict dominating rules is up to \(\left( ^{n}_{1}\right) \times 2^{e}\). Similarly, the number of 2-antecedent strict dominating rules is up to \(\left( ^{n}_{2}\right) \times 2^{e}\). Therefore, the number of strict dominating rules for (\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)) \(\rightarrow \) (\(\hbox {C}_{1}\):\(\hbox {C}_{m}\)) is up to \(2^{n+e}\).
In the context of complete rules, for each additional item, there are 3 possibilities (positive form, negative form, not chosen). Therefore, there are \(3^{e}\) possibilities for adding items from e additional items to the consequent. The number of strict dominating rules for (\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)) \(\rightarrow \) (\(\hbox {C}_{1}\):\(\hbox {C}_{m}\)) is up to \(2^{n}\times 3^{e}\). \(\square \)
1.7 Proof of Lemma 15
Proof
Within the strict dominating rule set \(\{{\mathcal {R}}^{\gg _{str}}\}\), the strict dominating rules formed by adding one item \(C_{h}\) to the consequent have larger or equal support value than the strict dominating rules formed by adding the same item \(C_{h}\) plus one more item \(C_{g}\) to the consequent, with \(C_{h}\) and \(C_{g}\) each are a single item out of the set {\(\hbox {C}_{m+1}\):\(\hbox {C}_{m+e}\)}. That is, adding only one item into consequent of \({\mathcal {R}}\) tends to have the larger support value. Let us assume adding item \(C_{q}\) incurs the largest support value, namely, the rules based on the underlying itemset ((\(A_{1}\):\(A_{n}\)) \(\cup \) (\(C_{1}\):\(C_{m}\)) \(\cup \) \(C_{q}\)) have the highest support value among all other rules in the strict dominating rule set \(\{{\mathcal {R}}^{\gg _{str}}\}\). In fact, we note that these strict dominating rules composed by all items from the itemset ((\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)) \(\cup \) (\(\hbox {C}_{1}\):\(\hbox {C}_{m}\)) \(\cup \) \(\hbox {C}_{q}\)) have the same support value. They could have 1 to n items in the antecedent, namely, a subset of (\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)) as antecedent. The strict dominating rules with the largest confidence value would have all n items in its antecedent because its confidence equals Supp((\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)) \(\cup \) (\(\hbox {C}_{1}\):\(\hbox {C}_{m}\)) \(\cup \) \(\hbox {C}_{q}\)) / Supp(\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)). The denominator is the smallest when all n items are included. Thus the confidence value is the highest for the rule that is composed by items (\(A_{1}\):\(A_{n}\)) as antecedent and (\(C_{1}\):\(C_{m}\)) \(\cup \) \(C_{q}\) as consequent. The support and confidence value of rule ((\(A_{1}\):\(A_{n}\)) \(\rightarrow \) (\(C_{1}\):\(C_{m}\)) \(\cup \) \(C_{q}\)) is the strict dominating location \(\ell ^{\gg _{str}}\) of \({\mathcal {R}}\). \(\square \)
1.8 Proof of Theorem 1
Proof
Since the result rule set \(\{{\mathcal {R}}\}\) is derived from the query using parameter values (minsup, minconf), the coordinate of each rule \({\mathcal {R}}\) in the result set \(\{{\mathcal {R}}\}\) must be larger than the user provided parameter (minsup, minconf), namely, minsupp \(\le \) \({\mathcal {R}}.supp\) and minconf \(\le \) \({\mathcal {R}}.conf\). Three possible scenarios are present below:
Case 1: The rule with the highest support and confidence value in the strict dominating rule set of \({\mathcal {R}}\) is located in the strict dominating location of \({\mathcal {R}}\) by Lemma 15. If both of the user given parameter settings are lower than or equal to the strict dominating location’s coordinate, namely, \(minsupp\le \) \(\ell ^{\gg _{str}}\).supp AND \(minconf\le \) \(\ell ^{\gg _{str}}\).conf, then one or more strict dominating rules of \({\mathcal {R}}\) are valid. This would make \({\mathcal {R}}\) redundant.
Case 2: The rule with the highest confidence value in the simple dominating rule set of \({\mathcal {R}}_{j}\) is located in the simple dominating location of \({\mathcal {R}}_{j}\) by Lemma 11. If both of the user given parameter settings are lower than or equal to the simple dominating location’s coordinate, namely, \(minsupp\le \ell ^{\gg _{sim}}\).supp AND \(minconf\le \) \(\ell ^{\gg _{sim}}\).conf, then one or more simple dominating rules of \({\mathcal {R}}\) are valid. This would make \({\mathcal {R}}\) redundant. Note that Case 1 and Case 2 are partial overlapping, meaning the user given parameter setting could be lower than both the simple and strict dominating location.
Case 3: If the minsupp parameter is greater than the strict dominating location’s support and the minconf parameter is greater than the simple dominating location’s confidence, namely, minsupp > \(\ell ^{\gg _{str}}.supp\) AND minconf > \(\ell ^{\gg _{sim}}.conf\), then none of dominating rules of \({\mathcal {R}}\) is valid. Thus \({\mathcal {R}}\) is not redundant.
\(\square \)
1.9 Proof of Theorem 2
Proof
We first assume that all top simple dominating rules are valid. We prove that it is necessary and sufficient to search only the top simple dominating rules.
Scenario 1: All top simple dominating rules are valid. “Necessary”: To find the top simple dominating location of \({\mathcal {R}}\), it is necessary to consider all the (n-1)-antecedent simple dominating rules as any one of them can be the simple dominating location (Lemma 11) depending on each of these simple dominating rules’ confidence.
“Sufficient”: We further prove the sufficiency as follows. For a rule \({\mathcal {R}}\): (\(\hbox {A}_{1}\):\(\hbox {A}_{n}\)) \(\rightarrow \) (\(\hbox {C}_{1}\):\(\hbox {C}_{m}\)) with n antecedents, all rules in the set of simple dominating rules \(\{{\mathcal {R}}^{\gg _{sim}}\}\) have the same support value as rule \({\mathcal {R}}\) by Lemma 2. However, their confidence values may differ. Next, we argue that the (n-1)-antecedent dominating rules have the largest confidence among all 2\(^{n}\)-2 simple dominating rules. Recall that the simple dominating rules conform to the template (((\(A_{1}\):\(A_{n}\))-(\(A_{v}\):\(A_{w}\))) \(\rightarrow \) ((\(A_{v}\):\(A_{w}\)) \(\cup \) (\(C_{1}\):\(C_{m}\)))). Thus the confidence for such a rule is given by the formula \(\frac{S((A_{1}:A_{n})\cup (C_{1}:C_{m}))}{S((A_{1}:A_{n})-(A_{v}:A_{w}))}\). The numerator is the same for all simple dominating rules, while the denominators differ. S((\(A_{1}\):\(A_{n}\))-\(A_{i}\)), where \(A_{i}\) is a single item, is the smallest denominator compared to all other rules that remove \(A_{i}\) in addition to any other \(A_{j}(1 \le j \le n)\). This then makes the confidence of rules (((\(A_{1}\):\(A_{n}\))-\(A_{i}\)) \(\rightarrow \) (\(A_{i}\cup \)(\(C_{1}\):\(C_{m}\)))) the highest among all simple dominating rules. Hence, the confidence of all (n-1)-antecedent simple dominating rules (aka top simple dominating rules) will be the highest. It is thus sufficient to only consider them instead of all 2\(^{n}\)-2 simple dominating rules.
Scenario 2: One or more top simple dominating rules are invalid.
We then consider the scenario that one or more top simple dominating rules are invalid. Suppose rule \({{\mathcal {R}}^{\gg _{sim}}}_{j}\) is one of the top simple dominating rules of rule \({\mathcal {R}}\). Suppose rule \({{\mathcal {R}}^{\gg _{sim}}}_{j}\) is an invalid rule, it could be invalid for two possible reasons: 1), it has insufficient support or confidence. 2), it has an insufficient lift.
For 1), we simply remove rule \({{\mathcal {R}}^{\gg _{sim}}}_{j}\) because its insufficient support or confidence indicates that all its simple dominating rules do not have sufficient support or confidence by Lem. 2. For 2), although rule \({{\mathcal {R}}^{\gg _{sim}}}_{j}\) is invalid due to insufficient lift, it is still possible that its simple dominating rules have sufficient lift. Therefore, one or more simple dominating rules of \({{\mathcal {R}}^{\gg _{sim}}}_{j}\) could be valid. These rules may have a higher confidence value than all valid simple dominating rules of \({\mathcal {R}}\). In this case, we cannot just remove rule \({{\mathcal {R}}^{\gg _{sim}}}_{j}\). Instead, we need to look for a valid simple dominating rule of rule \({{\mathcal {R}}^{\gg _{sim}}}_{j}\) which has the largest confidence value among all simple dominating rules of \({{\mathcal {R}}^{\gg _{sim}}}_{j}\). In other words, we need the simple dominating location of \({{\mathcal {R}}^{\gg _{sim}}}_{j}\) to participate in the comparisons with all valid top simple dominating rules of rule \({\mathcal {R}}\) because the simple dominating location of \({{\mathcal {R}}^{\gg _{sim}}}_{j}\) represents the largest support and confidence values of \({{\mathcal {R}}^{\gg _{sim}}}_{j}\)’s simple dominating rules. Below we prove that it is necessary and sufficient to search only the top simple dominating rules in scenario 2.
“Necessary”: same as Scenario 1.
“Sufficient”: For the simple dominating rule set \(\{{\mathcal {R}}^{\gg _{sim}}\}\) of rule \({\mathcal {R}}\), suppose 1) rule \({{\mathcal {R}}^{\gg _{sim}}}_{j}\) \(\in \) \(\{{\mathcal {R}}^{\gg _{sim}}\}\); 2) rule \({{\mathcal {R}}^{\gg _{sim}}}_{j}\) is a top simple dominating rule of rule \({\mathcal {R}}\); 3) \({{\mathcal {R}}^{\gg _{sim}}}_{j}\) is an invalid rule as it has sufficient support/confidence yet insufficient lift. The simple dominating location of \({{\mathcal {R}}^{\gg _{sim}}}_{j}\) saves the largest support and confidence value which \({{\mathcal {R}}^{\gg _{sim}}}_{j}\)’s simple dominating rules have. Meanwhile, each valid top simple dominating rule’s confidence value is greater than its respective simple dominating rules. Therefore, the simple dominating location(s) of invalid top simple dominating rule(s) and the support and confidence values of valid top simple dominating rules complete the candidate set for computing simple dominating location for \({\mathcal {R}}\). \(\square \)
1.10 Proof of Theorem 3
Proof
We first assume all top strict dominating rules are valid.
Scenario 1: All top strict dominating rules are valid.
“Necessary”: We first prove the necessity as below. For the strict dominating rules of \({\mathcal {R}}\) formed by including additional item \(C_{h}\) beyond the items from \({\mathcal {R}}\) into the consequent, namely, the top strict dominating rules, it cannot be decided which of them has the highest support and confidence value without inspecting each. Thus, we need to examine every top strict dominating rule of \({\mathcal {R}}\) to determine the strict dominating location.
“Sufficient”: We further prove the sufficiency as follows. For a rule \({\mathcal {R}}\): (\(A_{1}\):\(A_{n}\)) \(\rightarrow \) (\(C_{1}\):\(C_{m}\)), the rules in the strict dominating rule set \(\{{\mathcal {R}}^{\gg _{str}}\}\) have the underlying itemset containing all items (\(A_{1}\):\(A_{n}\)) \(\cup \) (\(C_{1}\):\(C_{m}\)) from rule \({\mathcal {R}}\) and a subset of items from (\(C_{h}\):\(C_{h+e}\)) beyond rule \({\mathcal {R}}\). Among them the rule formed by adding only one item from (\(C_{h}\):\(C_{h+e}\)) tends to have a larger support value than the rule formed by adding more than one item, namely, Supp((\(A_{1}\):\(A_{n}\)) \(\cup \) (\(C_{1}\):\(C_{m}\)) \(\cup \) \(C_{h}\)) \(\ge \) Supp((\(A_{1}\):\(A_{n}\)) \(\cup \) (\(C_{1}\):\(C_{m}\)) \(\cup \) \(C_{h}\) \(\cup \) \(C_{h'}\) \(\cup \) \(\ldots )\). Assume here that adding item \(C_{h}\) to rule \({\mathcal {R}}\) would bring us the largest support value compared to choosing another item. Then the strict dominating rules composed of all items from the itemset ((\(A_{1}\):\(A_{n}\)) \(\cup \) (\(C_{1}\):\(C_{m}\)) \(\cup \) \(C_{h}\)) have the same support value. They could have 1 to n items as the antecedent, namely, a subset of (\(A_{1}\):\(A_{n}\)) as antecedent. This leads to the fact that each rule may have different confidence values. The strict dominating rules with the largest confidence value would have all n items in the antecedent because its confidence equals Supp((\(A_{1}\):\(A_{n}\)) \(\cup \) (\(C_{1}\):\(C_{m}\)) \(\cup \) \(C_{h}\)) / Supp(\(A_{1}\):\(A_{n}\)). The denominator is the smallest when all n items are included. Thus the confidence value is the largest for the rule that is composed of the itemset ((\(A_{1}\):\(A_{n}\)) \(\cup \) (\(C_{1}\):\(C_{m}\)) \(\cup \) \(C_{h}\)). Thus, it is necessary and sufficient to consider all top strict dominating rules.
Scenario 2: One or more top strict dominating rules are invalid.
“Necessary”: Same as Scenario 1.
“Sufficient”: For the strict dominating rule set \(\{{\mathcal {R}}^{\gg _{str}}\}\) of rule \({\mathcal {R}}\), suppose 1) rule \({{\mathcal {R}}^{\gg _{str}}}_{k}\) \(\in \) \(\{{\mathcal {R}}^{\gg _{str}}\}\); 2) rule \({{\mathcal {R}}^{\gg _{str}}}_{k}\) is a top strict dominating rule of rule \({\mathcal {R}}\); 3) \({{\mathcal {R}}^{\gg _{str}}}_{k}\) is an invalid rule as it has sufficient support/confidence yet insufficient lift. The strict dominating location of \({{\mathcal {R}}^{\gg _{str}}}_{k}\) records the largest support and confidence value that \({{\mathcal {R}}^{\gg _{str}}}_{k}\)’s simple dominating rules and strict dominating rules have. Meanwhile, each valid top strict dominating rule’s support and confidence values are larger than its respective simple/strict dominating rules. Thus, the strict dominating location(s) of invalid top strict dominating rule(s) and the (support, confidence) values of valid top strict dominating rule(s) comprise the strict dominating location candidate set for computing strict dominating location for \({\mathcal {R}}\). The largest (support, confidence) among the strict dominating location candidate set is the largest values among all strict dominating rule’s location. It is thus sufficient to only search the top strict dominating rules. \(\square \)
Rights and permissions
About this article
Cite this article
Lin, X., Mukherji, A., Rundensteiner, E.A. et al. PARAS\(^{\mathrm{c}}\): a parameter space-driven approach for complete association rule mining. Int J Data Sci Anal 14, 407–438 (2022). https://doi.org/10.1007/s41060-022-00330-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41060-022-00330-3