Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-04-30T11:10:21.377Z Has data issue: false hasContentIssue false
  • English
  • Français

On some properties of distributions possessing a bathtub-shaped failure rate average

Part of: Special processes Survival analysis and censored data

Published online by Cambridge University Press:  04 January 2023

Ruhul Ali Khan Open the ORCID record for Ruhul Ali Khan [Opens in a new window] ,
Dhrubasish Bhattacharyya  and
Murari Mitra
Ruhul Ali Khan*
Affiliation:
Indian Institute of Engineering Science and Technology, Shibpur
Dhrubasish Bhattacharyya*
Affiliation:
Indian Statistical Institute, Kolkata
Murari Mitra*
Affiliation:
Indian Institute of Engineering Science and Technology, Shibpur
*
*Postal address: Department of Mathematics, Indian Institute of Engineering Science and Technology, Shibpur, P.O. -Botanic Garden, Howrah- 711103, West Bengal, India.
****Postal address: Applied Statistics Unit, Indian Statistical Institute, 203, B. T. Road, Kolkata 700108, India. Email address: dhrubasish018@gmail.com
*Postal address: Department of Mathematics, Indian Institute of Engineering Science and Technology, Shibpur, P.O. -Botanic Garden, Howrah- 711103, West Bengal, India.
Get access Rights & Permissions [Opens in a new window]

Abstract

The life distribution of a device subject to shocks governed by a homogeneous Poisson process is shown to have a bathtub failure rate average (BFRA) when the probabilities 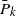$\bar{P}_k$ of surviving k shocks possess the corresponding discrete property. We prove closure under the formation of weak limits for BFRA distributions and explore related moment convergence issues within the BFRA family. Similar results for increasing and decreasing failure rate average distributions are obtained either independently or as consequences of our results. We also establish some results outlining the positions of various non-monotonic ageing classes such as bathtub failure rate, increasing initially then decreasing mean residual life, new worse then better than used in expectation, and increasing initially then decreasing mean time to failure in the hierarchy. Finally, an open problem is posed and a partial solution provided.

Keywords

Failure rate average functionchange pointBFRA classhomogeneous Poisson shock modelweak convergenceinterrelationships

MSC classification

Primary: 62N05: Reliability and life testing
Secondary: 60K10: Applications (reliability, demand theory, etc.)
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 2 , June 2023 , pp. 693 - 708
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aarset, M. V. (1987). How to identify a bathtub hazard rate. IEEE Trans. Reliab. 36, 106–108.CrossRefGoogle Scholar
Abouammoh, A., Hindi, M. and Ahmed, A. (1988). Shock models with NBUFR and NBAFR survivals. Trabajos de Estadistica 3, 97.CrossRefGoogle Scholar
Anderson, K. K. (1987). Limit theorems for general shock models with infinite mean intershock times. J. Appl. Prob. 24, 449–456.CrossRefGoogle Scholar
Anis, M. (2012). On some properties of the IDMRL class of life distributions. J. Statist. Planning Infer. 142, 3047–3055.CrossRefGoogle Scholar
Bandyopadhyay, D. and Basu, A. P. (1989). A note on tests for exponentiality by Deshpande. Biometrika 76, 403–405.10.1093/biomet/76.2.403CrossRefGoogle Scholar
Barlow, R. E. (1979). Geometry of the total time on test transform. Naval Res. Logistics Quart. 26, 393–402.CrossRefGoogle Scholar
Barlow, R. E. and Proschan, F. (1965). Mathematical Theory of Reliability. Wiley, New York.Google Scholar
Barlow, R. E. and Proschan, F. (1981). Statistical Theory of Reliability and Life Testing. To Begin With, Silver Spring, MD.Google Scholar
Basu, S. K. and Bhattacharjee, M. C. (1984). On weak convergence within the HNBUE family of life distributions. J. Appl. Prob. 21, 654–660.CrossRefGoogle Scholar
Basu, S. K. and Simons, G. (1982). Moment spaces for IFR distributions: Applications and related material. In Contributions to Statistics. Essays in Honour of Norman L. Johnson, ed Sen, P. K.. Holland, North, Amsterdam.Google Scholar
Bennett, S. (1983). Log-logistic regression models for survival data. J. R. Statist. Soc. C [Appl. Statist.] 32, 165–171.Google Scholar
Bhattacharyya, D., Ghosh, S. and Mitra, M. (2020). On a non-monotonic ageing class based on the failure rate average. Commun. Statist. Theory Meth. 51, 4807–4826.CrossRefGoogle Scholar
Bhattacharyya, D., Khan, R. A. and Mitra, M. (2020). A test of exponentiality against DMTTF alternatives via L-statistics. Statist. Prob. Lett. 165, 108853.CrossRefGoogle Scholar
Bhattacharyya, D., Khan, R. A. and Mitra, M. (2021). A goodness of fit test for mean time to failure function in age replacement. J. Statist. Comput. Simul. 91, 3637–3652.CrossRefGoogle Scholar
Bhattacharyya, D., Khan, R. A. and Mitra, M. (2021). Two-sample nonparametric test for comparing mean time to failure functions in age replacement. J. Statist. Planning Infer. 212, 34–44.CrossRefGoogle Scholar
Birnbaum, Z. W., Esary, J. D. and Marshall, A. (1966). A stochastic characterization of wear-out for components and systems. Ann. Math. Statist. 37. 816–825.CrossRefGoogle Scholar
Boland, P. J. and Proschan, F. (1983). Optimum replacement of a system subject to shocks. Operat. Res. 31, 697–704.CrossRefGoogle Scholar
Deshpande, J. V., Kochar, S. C. and Singh, H. (1986). Aspects of positive ageing. J. Appl. Prob. 23. 748–758.CrossRefGoogle Scholar
Ebrahimi, N. (1999). Stochastic properties of a cumulative damage threshold crossing model. J. Appl. Prob. 36, 720–732.CrossRefGoogle Scholar
El-Neweihi, E., Proschan, F. and Sethuraman, J. (1983). A multivariate new better than used class derived from a shock model. Operat. Res. 31, 177–183.CrossRefGoogle Scholar
Esary, J. D. and Marshall, A. (1974). Families of components, and systems, exposed to a compound Poisson damage process. In Reliability and Biometry: Statistical Analysis of Life Length, eds F. Proschan and R. J. Serfling. SIAM, Philadelphia, PA, pp. 31–46.Google Scholar
Esary, J., Marshall, A. and Proschan, F. (1973). Shock models and wear processes. Ann. Prob. 1, 627–649.CrossRefGoogle Scholar
Glaser, R. E. (1980). Bathtub and related failure rate characterizations. J. Amer. Statist. Assoc. 75, 667–672.CrossRefGoogle Scholar
Guess, F., Hollander, M. and Proschan, F. (1986). Testing exponentiality versus a trend change in mean residual life. Ann. Statist. 14, 1388–1398.10.1214/aos/1176350165CrossRefGoogle Scholar
Gupta, R. C. and Warren, R. (2001). Determination of change points of non-monotonic failure rates. Commun. Statist. Theory Meth. 30, 1903–1920.CrossRefGoogle Scholar
Izadi, M. and Manesh, S. F. (2019). Testing exponentiality against a trend change in mean time to failure in age replacement. Commun. Statist. Theory Meth. 50, 3358–3370.CrossRefGoogle Scholar
Izadi, M., Sharafi, M. and Khaledi, B.-E. (2018). New nonparametric classes of distributions in terms of mean time to failure in age replacement. J. Appl. Prob. 55, 1238–1248.CrossRefGoogle Scholar
Joe, H. and Proschan, F. (1984). Percentile residual life functions. Operat. Res. 32, 668–678.CrossRefGoogle Scholar
Karlin, S. (1968). Total Positivity, Vol. 1. Stanford University Press.Google Scholar
Khan, R. A., Bhattacharyya, D. and Mitra, M. (2020). A change point estimation problem related to age replacement policies. Operat. Res. Lett. 48, 105–108.CrossRefGoogle Scholar
Khan, R. A., Bhattacharyya, D. and Mitra, M. (2021). Exact and asymptotic tests of exponentiality against nonmonotonic mean time to failure type alternatives. Statist. Papers 62, 3015–3045.CrossRefGoogle Scholar
Khan, R. A., Bhattacharyya, D. and Mitra, M. (2021). On classes of life distributions based on the mean time to failure function. J. Appl. Prob. 58, 289–313.CrossRefGoogle Scholar
Khan, R. A., Bhattacharyya, D. and Mitra, M. (2021). On some properties of the mean inactivity time function. Statist. Prob. Lett. 170, 108993.CrossRefGoogle Scholar
Khan, R. A. and Mitra, M. (2019). Sharp bounds for survival probability when ageing is not monotone. Prob. Eng. Inf. Sci. 33, 205–219.CrossRefGoogle Scholar
Klefsjö, B. (1981). HNBUE survival under some shock models. Scand. J. Statist., 8, 39–47.Google Scholar
Klefsjö, B. (1982). On aging properties and total time on test transforms. Scand. J. Statist., 9, 37–41.Google Scholar
Klefsjö, B. (1983). Some tests against aging based on the total time on test transform. Commun. Statist. Theory Meth. 12, 907–927.CrossRefGoogle Scholar
Klefsjö, B. (1983). A useful ageing property based on the Laplace transform. J. Appl. Prob. 20, 615–626.CrossRefGoogle Scholar
Kochar, S. C. (1985). Testing exponentiality against monotone failure rate average. Commun. Statist. Theory Meth. 14, 381–392.CrossRefGoogle Scholar
Kochar, S. C. (1990) On preservation of some partial orderings under shock models. Adv. Appl. Prob. 22, 508–509.CrossRefGoogle Scholar
Lai, C. D. and Xie, M. (2006). Stochastic Ageing and Dependence for Reliability. Springer, New York.Google Scholar
Langlands, A. O., Pocock, S. J., Kerr, G. and Gore, S. M. (1979). Long term survival of patients with breast cancer: A study of the curability of the disease. British Med. J., 2, 1247–1251.CrossRefGoogle ScholarPubMed
Link, W. A. (1989). Testing for exponentiality against monotone failure rate average alternatives. Commun. Statist. Theory Meth. 18. 3009–3017.CrossRefGoogle Scholar
Loève, M. (1963). Probability Theory, 3rd edn. Van Nostrand, New York.Google Scholar
Mi, J. (1993). Discrete bathtub failure rate and upside-down bathtub mean residual life. Naval Res. Logistics 40, 361–371.10.1002/1520-6750(199304)40:3<361::AID-NAV3220400306>3.0.CO;2-I3.0.CO;2-I>CrossRefGoogle Scholar
Mi, J. (1995). Bathtub failure rate and upside-down bathtub mean residual life. IEEE Trans. Reliab. 44, 388–391.Google Scholar
Mitra, M. and Basu, S. K. (1994). On a nonparametric family of life distributions and its dual. J. Statist. Planning Infer. 39, 385–397.CrossRefGoogle Scholar
Mitra, M. and Basu, S. K. (1996). On some properties of the bathtub failure rate family of life distributions. Microelectron. Reliab. 36, 679–684.CrossRefGoogle Scholar
Mitra, M. and Basu, S. K. (1996). Shock models leading to non-monotonic ageing classes of life distributions. J. Statist. Planning Infer. 55, 131–138.CrossRefGoogle Scholar
Mitra, M. and Khan, R. A. (2021). Reliability shock models: A brief excursion. In Applied Advanced Analytics, ed A. K. Laha. Springer, Singapore, pp. 19–42.CrossRefGoogle Scholar
Nakagawa, T. (2007). Shock and Damage Models in Reliability Theory. Springer, New York.Google Scholar
Neath, A. A. and Samaniego, F. J. (1992). On the total time on test transform of an IFRA distribution. Statist. Prob. Lett. 14, 289–291.CrossRefGoogle Scholar
Pellerey, F. (1993). Partial orderings under cumulative damage shock models. Adv. Appl. Prob. 25, 939–946.CrossRefGoogle Scholar
Prentice, R. L. (1973). Exponential survivals with censoring and explanatory variables. Biometrika 60, 279–288.CrossRefGoogle Scholar
Shanthikumar, J. G. and Sumita, U. (1983). General shock models associated with correlated renewal sequences. J. Appl. Prob. 20, 600–614.CrossRefGoogle Scholar
Singpurwalla, N. D. (2006). The hazard potential: Introduction and overview. J. Amer. Statist. Assoc. 101, 1705–1717.CrossRefGoogle Scholar
Tiwari, R. C., Rao Jammalamadaka, S. and Zalkikar, J. N. (1989). Testing an increasing failure rate average distribution with censored data. Statistics 20, 279–286.Google Scholar
Wang, F. (2000). A new model with bathtub-shaped failure rate using an additive Burr XII distribution. Reliab. Eng. Syst. Saf. 70, 305–312.CrossRefGoogle Scholar
Wells, M. T. and Tiwari, R. C. (1991). A class of tests for testing an increasing failure-rate-average distribution with randomly right-censored data. IEEE Trans. Reliab. 40, 152–156.CrossRefGoogle Scholar