Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-05-18T21:00:37.505Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPLEXITY OF INDEX SETS OF DESCRIPTIVE SET-THEORETIC NOTIONS

Part of: Computability and recursion theory Set theory

Published online by Cambridge University Press:  10 January 2022

REESE JOHNSTON  and
DILIP RAGHAVAN
REESE JOHNSTON
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN – MADISONMADISON, WI53715,USA Current address: ROBINSON CENTER FOR YOUNG SCHOLARS UNIVERSITY OF WASHINGTON 3950 BENTON LN NE, SEATTLE, WA98195, USAE-mail:reesej2@uw.edu
DILIP RAGHAVAN
Affiliation:
DEPARTMENT OF MATHEMATICS NATIONAL UNIVERSITY OF SINGAPORE 21 LOWER KENT RIDGE ROAD, SINGAPOREE-mail:matrd@nus.edu.sg
Get access Rights & Permissions [Opens in a new window]

Abstract

Descriptive set theory and computability theory are closely-related fields of logic; both are oriented around a notion of descriptive complexity. However, the two fields typically consider objects of very different sizes; computability theory is principally concerned with subsets of the naturals, while descriptive set theory is interested primarily in subsets of the reals. In this paper, we apply a generalization of computability theory, admissible recursion theory, to consider the relative complexity of notions that are of interest in descriptive set theory. In particular, we examine the perfect set property, determinacy, the Baire property, and Lebesgue measurability. We demonstrate that there is a separation of descriptive complexity between the perfect set property and determinacy for analytic sets of reals; we also show that the Baire property and Lebesgue measurability are both equivalent in complexity to the property of simply being a Borel set, for 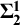$\boldsymbol {\Sigma ^{1}_{2}}$ sets of reals.

Keywords

computabilityadmissible recursiondescriptive set theoryBaire propertyLebesgue measureBorel set

MSC classification

Primary: 03D60: Computability and recursion theory on ordinals, admissible sets, etc.
Secondary: 03E15: Descriptive set theory
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 3 , September 2022 , pp. 894 - 911
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chong, C.-T., Techniques of Admissible Recursion Theory, Springer, New York, 1984.CrossRefGoogle Scholar
van Engelen, F., Miller, A. W., and Steel, J., Rigid borel sets and better quasi-order theory, Logic and Combinatorics, Contemporary Mathematics, American Mathematical Society, Providence, RI, 1987, pp. 199–222.10.1090/conm/065/891249CrossRefGoogle Scholar
Erdös, P., Kunen, K., and Mauldin, R., Some additive properties of sets of real numbers . Fundamenta Mathematicae, vol. 113 (1981), no. 3, pp. 187–199.CrossRefGoogle Scholar
Fischer, V. and Törnquist, A., A co-analytic maximal set of orthogonal measures , this Journal, vol. 75 (2010), no. 04, pp. 1403–1414.Google Scholar
Greenberg, N. and Knight, J. F., Computable structure theory using admissible recursion theory on ${\omega}_1$ using admissibility, Effective Mathematics of the Uncountable, Cambridge University Press, Cambridge, 2013, pp. 50–80.10.1017/CBO9781139028592.005CrossRefGoogle Scholar
Kanamori, A., The Higher Infinite: Large Cardinals in Set Theory from their Beginnings, World Publishing Corporation, 2011.Google Scholar
Kastermans, B., The complexity of maximal cofinitary groups. Proceedings of the American Mathematical Society, vol. 137 (2009), no. 1, pp. 307–316.CrossRefGoogle Scholar
Kechris, A. S., Classical Descriptive Set Theory, Springer, New York, 2012.Google Scholar
Kleene, S. C., Quantification of number-theoretic functions. Compositio Mathematica, vol. 14 (1960), pp. 23–40.Google Scholar
Kripke, S., Transfinite recursion on admissible ordinals I, II (abstracts) , this Journal, vol. 29 (1964), pp. 161–162.Google Scholar
Miller, A. W., Infinite combinatorics and definability. Annals of Pure and Applied Logic, vol. 41 (1989), no. 2, pp. 179–203.CrossRefGoogle Scholar
Soare, R. I., Turing Computability: Theory and Applications, Springer, New York, 2016.CrossRefGoogle Scholar
Tomek, B. and Judah, H., Set Theory: On the Structure of the Real Line, A. K. Peters, Wellesley, MA, 1999.Google Scholar