We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 12 March 2014
In the paper we prove the following theorem:
Theorem. There is a model N of open induction in which the set of primes is bounded and N is such that its field of fractions 〈N*, +, ·, <〉 is elementarily equivalent to 〈Q, +, ·, <〉 (the standard rationals).
We fix an ω 1-saturated model 〈M, +, ·, <〉 of PA. Let 〈M*, +, ·, <〉 denote the field of fractions of M. The model N that we are looking for will be a substructure of 〈M*, +, ·, <〉.
If A ⊆ M* then let Ā denote the ring generated by A within M*, Ậ the real closure of A, and A* the field of fractions generated by A. We have
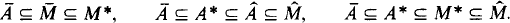
Let J ⊆ M. Then 〈M*, +, ·〉 is a linear space over J*. If x 1,…,xk ∈ M*, we shall say that x 1,…,xk are J-independent if 〈1, x 1,…, xk 〉 are J*-independent in the usual sense. As usual, we extend the notion of J-independence to the case of infinite sets.
If A ⊆ M* and X ⊆ A, then we say that X is a J-basis of A if X is a maximal subset of A which is J-independent.
