Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-26T17:01:00.925Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit laws for large 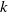$k$th-nearest neighbor balls

Part of: Geometric probability and stochastic geometry Limit theorems Stochastic processes

Published online by Cambridge University Press:  06 July 2022

Nicolas Chenavier ,
Norbert Henze  and
Moritz Otto
Nicolas Chenavier*
Affiliation:
Université du Littoral Côte d’Opale
Norbert Henze*
Affiliation:
Karlsruhe Institute of Technology (KIT)
Moritz Otto*
Affiliation:
Otto von Guericke University Magdeburg
*
*Postal address: 50 rue Ferdinand Buisson, 62228 Calais, France. Email address: nicolas.chenavier@univ-littoral.fr
**Postal address: Englerstr. 2, D-76133 Karlsruhe, Germany. Email address: Norbert.Henze@kit.edu
***Postal address: Aarhus University, Ny Munkegade 118, 8000 Aarhus C, Denmark. Email address: otto@math.au.dk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 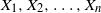$X_1,X_2, \ldots, X_n$ be a sequence of independent random points in 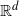$\mathbb{R}^d$ with common Lebesgue density f. Under some conditions on f, we obtain a Poisson limit theorem, as 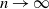$n \to \infty$ , for the number of large probability kth-nearest neighbor balls of 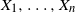$X_1,\ldots, X_n$ . Our result generalizes Theorem 2.2 of [11], which refers to the special case 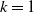$k=1$ . Our proof is completely different since it employs the Chen–Stein method instead of the method of moments. Moreover, we obtain a rate of convergence for the Poisson approximation.

Keywords

Binomial point processlarge kth nearest neighbor ballsChen–Stein methodPoisson convergenceGumbel distribution

MSC classification

Primary: 60F05: Central limit and other weak theorems
Secondary: 60D05: Geometric probability and stochastic geometry 60G70: Extreme value theory; extremal processes
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 3 , September 2022 , pp. 880 - 894
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahsanullah, M., Nevzzorov, V. B. and Shakil, M. (2013). An Introduction to Order Statistics. Atlantis Press, Amsterdam, Paris, and Beijing.10.2991/978-94-91216-83-1CrossRefGoogle Scholar
Arratia, R., Goldstein, L. and Gordon, L. (1990). Poisson approximation and the Chen–Stein method. Statist. Sci. 5, 403–434.Google Scholar
Avram, F. and Bertsimas, D. (1993). On central limit theorems in geometrical probability. Ann. Appl. Prob. 3, 1033–1046.10.1214/aoap/1177005271CrossRefGoogle Scholar
Biau, G. and Devroye, L. (2015). Lectures on the Nearest Neighbor Method. Springer, New York.10.1007/978-3-319-25388-6CrossRefGoogle Scholar
Bobrowski, O., Schulte, M. and Yogeshwaran, D. (2021). Poisson process approximation under stabilization and Palm coupling. Available at arXiv:2104.13261.Google Scholar
Bonnet, G. and Chenavier, N. (2020). The maximal degree in a Poisson–Delaunay graph. Bernoulli 26, 948–979.10.3150/19-BEJ1123CrossRefGoogle Scholar
Chenavier, N. and Robert, C. Y. (2018). Cluster size distributions of extreme values for the Poisson–Voronoi tessellation. Ann. Appl. Prob. 28, 3291–3323.10.1214/17-AAP1345CrossRefGoogle Scholar
Dette, H. and Henze, N. (1989). The limit distribution of the largest nearest-neighbour link in the unit d-cube. J. Appl. Prob. 26, 67–80.10.2307/3214317CrossRefGoogle Scholar
Dette, H. and Henze, N. (1990). Some peculiar boundary phenomena for extremes of rth nearest neighbor links. Statist. Prob. Lett. 10, 381–390.10.1016/0167-7152(90)90018-3CrossRefGoogle Scholar
Embrechts, P., Klüppelberg, C. and Mikosch, T. (1997). Modelling Extremal Events. Springer, New York.10.1007/978-3-642-33483-2CrossRefGoogle Scholar
Györfi, L., Henze, N. and Walk, H. (2019). The limit distribution of the maximum probability nearest neighbor ball. J. Appl. Prob. 56, 574–589.10.1017/jpr.2019.37CrossRefGoogle Scholar
Henze, N. (1982). The limit distribution for maxima of ‘weighted’ rth-nearest-neighbour distances. J. Appl. Prob. 19, 344–354.10.2307/3213486CrossRefGoogle Scholar
Henze, N. (1983). Ein asymptotischer Satz über den maximalen Minimalabstand von unabhängigen Zufallsvektoren mit Anwendung auf einen Anpassungstest im $\mathbb{R}^p$ und auf der Kugel [An asymptotic theorem on the maximum minimum distance of independent random vectors, with application to a goodness-of-fit test in $\mathbb{R}^p$ and on the sphere]. Metrika 30, 245–259 (in German).10.1007/BF02056931CrossRefGoogle Scholar
Joag-Dev, K. and Proschan, F. (1983). Negative association of random variables with applications. Ann. Statist. 11, 286–295.10.1214/aos/1176346079CrossRefGoogle Scholar
Last, G. and Penrose, M. D. (2017). Lectures on the Poisson Process (IMS Textbook). Cambridge University Press.10.1017/9781316104477CrossRefGoogle Scholar
Otto, M. (2020). Poisson approximation of Poisson-driven point processes and extreme values in stochastic geometry. Available at arXiv:2005.10116.Google Scholar
Penrose, M. D. (1997). The longest edge of the random minimal spanning tree. Ann. Appl. Prob. 7, 340–361.10.1214/aoap/1034625335CrossRefGoogle Scholar
Penrose, M. D. (2003). Random Geometric Graphs (Oxford Studies in Probability 5). Oxford University Press.Google Scholar
Schilling, J., and Henze, N. (2021). Two Poisson limit theorems for the coupon collector’s problem with group drawings. J. Appl. Prob. 58, 966–977.10.1017/jpr.2021.15CrossRefGoogle Scholar
Zubkov, A. N. and Orlov, O. P. (2018). Limit distributions of extremal distances to the nearest neighbor. Discrete Math. Appl. 28, 189–199.10.1515/dma-2018-0018CrossRefGoogle Scholar